牛客周赛 Round 20 解题报告 | 珂学家 | 状压DP/矩阵幂优化 + 前缀和的前缀和

---

前言

---

整体评价

这场比赛很特别，是牛客周赛的第20场，后两题难度直线飙升了。

前四题相对简单，E题是道状压题，历来状压题都难，F题压轴难题了，感觉学到了不少。

---

A. 赝品

先求的最大值

然后统计非最大值的个数，即可。

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));

        int n = sc.nextInt();
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = sc.nextInt();
        }

        // 获取数组的最大值
        int maxValue = Arrays.stream(arr).max().getAsInt();
        // 过滤最大值，并计数
        System.out.println(Arrays.stream(arr).filter(x -> x != maxValue).count());
    }

}

---

B. 小红的01连续段

状态机DP

令opt[n][2], 0表示第n字母以0结尾，往前扩展的最长连续0子串的数量，1状态亦是如此定义。

则遇到‘0’， ‘1’， ‘?’, 会有不同的转移

最后的结果为

$ma{x}_{i=0}^{i=n?1}(opt[i][s]),s\in (0,1)$

这边可以滚动优化，使得时间复杂度降为2个变量

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        String s = sc.next();

        int res = 0;
        int s0 = 0, s1 = 0;
        for (char c: s.toCharArray()) {
            if (c == '0') {
                s0++;
                s1 = 0;
            } else if (c == '1') {
                s1++;
                s0 = 0;
            } else {
                // 遇到？号
                s0++;
                s1++;
            }
            res = Math.max(res, Math.max(s0, s1));
        }
        System.out.println(res);
    }
    
}

---

C. 小红的01串构造

这题挺有趣的

其实你只要观察到

111000100

110001100

这两个是等价的

即聚合的1从一个组，转移另一个组，不改变相邻的总对数

因此可以构造一个，所有相邻对数t都在第一个组中，然后多余的1，独立为一组

这样保证 t+1<=k && t+1 + (k - (t+1)) * 2 <= n, 必然有解

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int n = sc.nextInt(), k = sc.nextInt(), t = sc.nextInt();

        if (k > n || k - 1 < t) {
            System.out.println(-1);
        } else {
            int k1 = t + 1;
            int k2 = k - t - 1;
            if (k1 + k2 * 2 <= n) {
                StringBuilder sb = new StringBuilder();
                for (int i = 0; i < k1; i++) sb.append("1");
                for (int i = 0; i < k2; i++) sb.append("01");
                for (int i = k1 + k2 * 2; i < n; i++) sb.append("0");
                System.out.println(sb);
            } else {
                System.out.println(-1);
            }
        }
    }

}

---

D. 小红的数位删除

这题，其实题目少了一个重要的条件

最后a，b不能为0

1. 二进制枚举

因为只有9位数，所以可以使用二进制枚举

这样时间复杂度为 $O(2^9?2^9?9?9)=2?10^8$, 枚举常数小，在合理的范围内

• 从大到小枚举
• 引入剪枝

import java.io.*;
import java.util.*;
import java.util.function.BiFunction;

public class Main {

    public static void main(String[] args) {

        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        char[] astr = sc.next().toCharArray();
        char[] bstr = sc.next().toCharArray();

        int inf = Integer.MAX_VALUE;
        int n1 = astr.length, n2 = bstr.length;
        int ans = inf;

        BiFunction<Integer, char[], Integer> calculate = (s, str) -> {
            int val = 0;
            for (int t = 0; t < str.length; t++) {
                if ((s & (1 << t)) != 0) {
                    val = val * 10 + (str[t] - '0');
                }
            }
            return val;
        };

        for (int i = (1 << n1)  - 1; i > 0; i--) {
            int r1 = n1 - Integer.bitCount(i);
            if (r1 >= ans) continue;

            int a = calculate.apply(i, astr);
            if (a == 0) continue;

            for (int j = (1 << n2) - 1; j > 0; j--) {
                int r2 = n2 - Integer.bitCount(j);
                if (r1 + r2 >= ans) continue;
                int b = calculate.apply(j, bstr);
                if (b == 0) continue;
                if (a % b == 0 || b % a == 0) {
                    ans = Math.min(ans, r1 + r2);
                }
            }
        }
        System.out.println(ans == inf ? -1 : ans);

    }

}

2. BFS解

这题的话，感觉还可以BFS，这样的话，找到解后可以立马退出。

---

E. 小红的漂亮串

思路: 状压DP

这题有’red’, 'der’限制，所以直接想O(1)求容斥解，行不通.

1. 正向状压解

回到状压的思路

引入5种状态

• 0, any是1,2,3,4以外的所有状态
• 1, 以r字母结尾
• 2，以d字母结尾
• 3，以re字母结尾
• 4，以de字母结尾

先聊下如何解决

Q: 子串不包含‘der’

只要在递推过程中, 对der的状态构造忽略即可

Q: 需要包含至少一个‘red’

额外引入一维的状态0/1, 表示当前字符串以包含red, 和暂时不包含red

---

设计好了状态, 以及解决思路

来看一下如何设计状态转移

令 dp[2][5], 前一维表示是否包含’red’, 后一维表示以什么结尾的状态

DP递推的话，以下两种都可以

• 填表法
• 刷表法

为啥要两者都介绍下呢？

主要是如果某一种实现，遇到了wa，这个时候可以用另一种思路去check/verify, 看看哪里的转移有遗漏。

状态迁移还是太多，这边选用一个 (0, 3)来分析，它涉及一个阶级跃迁

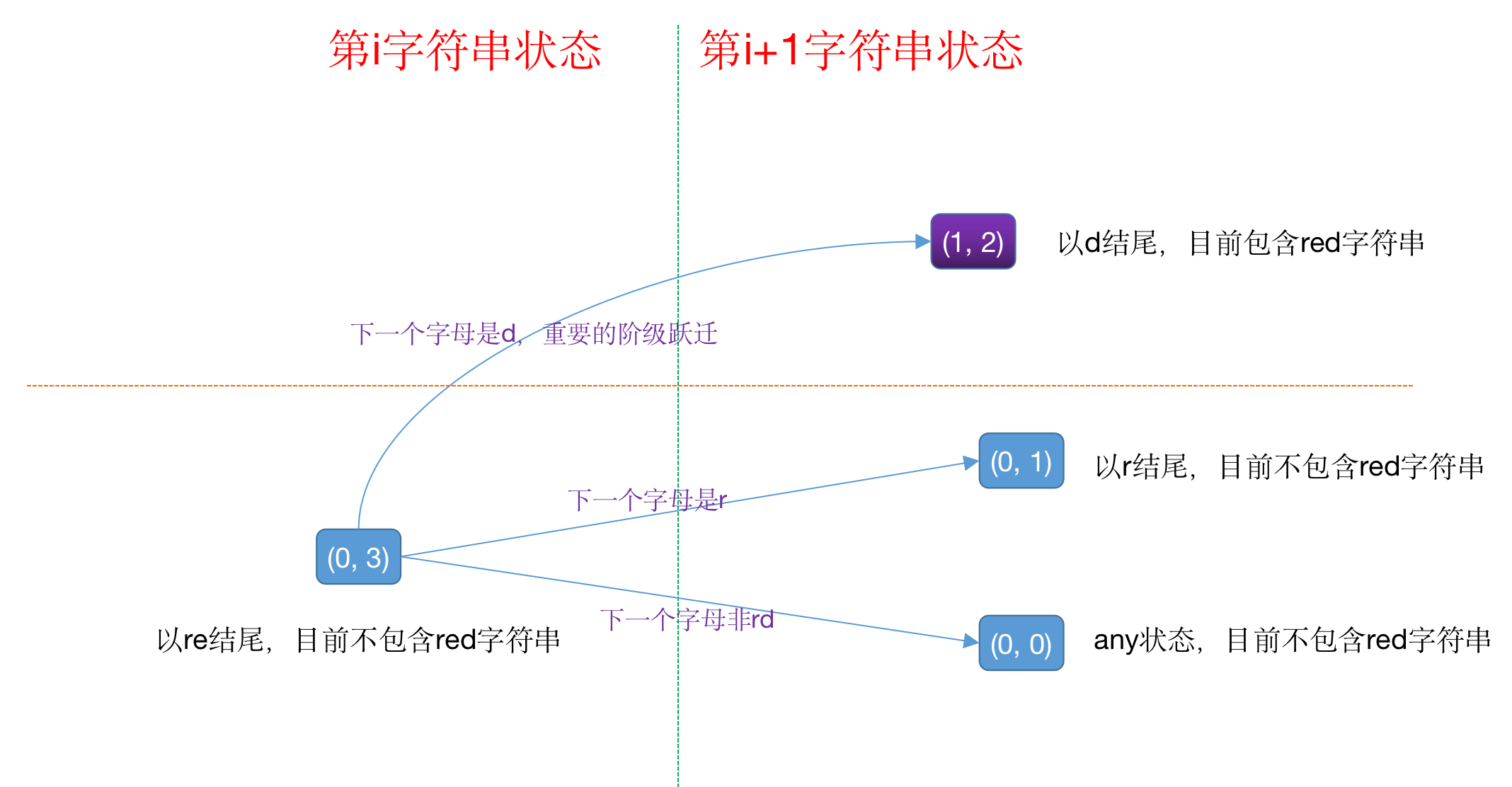
import java.io.BufferedInputStream;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int n = sc.nextInt();

        // any
        // r, d
        // re, de,
        long mod = 10_0000_0007l;

        // red, der
        long[][] dp = new long[2][5];
        dp[0][0] = 24;
        dp[0][1] = dp[0][2] = 1;

        for (int i = 1; i < n; i++) {
            long[][] dp2 = new long[2][5];

            // 不包含red字符串(在本身的圈子内转移)
            dp2[0][0] = (dp[0][0] * 24 % mod + dp[0][1] * 23 % mod + dp[0][2] * 23 % mod + dp[0][3] * 24 % mod + dp[0][4] * 24 % mod) % mod;
            dp2[0][1] = (dp[0][0] + dp[0][1] + dp[0][2] + dp[0][3]) % mod;
            dp2[0][2] = (dp[0][0] + dp[0][1] + dp[0][2] + dp[0][4]) % mod;
            dp2[0][3] = dp[0][1];
            dp2[0][4] = dp[0][2];

            // 包含red字符串(在本身的圈子内转移)
            dp2[1][0] = (dp[1][0] * 24 % mod + dp[1][1] * 23 % mod + dp[1][2] * 23 % mod + dp[1][3] * 24 % mod + dp[1][4] * 24 % mod) % mod;
            dp2[1][1] = (dp[1][0] + dp[1][1] + dp[1][2] + dp[1][3]) % mod;
            dp2[1][2] = (dp[1][0] + dp[1][1] + dp[1][2] + dp[1][3] + dp[1][4]) % mod;
            dp2[1][3] = dp[1][1];
            dp2[1][4] = dp[1][2];
            
            // 非常俏皮的阶级跃迁(最特别)，单独拎出来
            dp2[1][2] = (dp2[1][2] + dp[0][3]) % mod;

            dp = dp2;
        }

        // 只累加包含red字符串的状态
        long res = 0;
        for (int i = 0; i < 5; i++) {
            res += dp[1][i];
            res %= mod;
        }
        System.out.println(res);
    }

}

---

2. 容斥状压解

这题还可以容斥解，不过这个容斥解也是基于状压的

大致的思路

• 求解不存在der的字符串总个数S1
• 求解同时不存在der，red的字符串总个数S2
• S1 - S2, 即为不存在der，但是存在red的字符串总方案数

3. 矩阵幂优化

如果n在大点，n只要大于10^9，那矩阵幂才是唯一解

矩阵的构造，源于方法一，把2*5摊平成为1维

然后构建一个状态转移矩阵即可。

import java.io.BufferedInputStream;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int n = sc.nextInt();

        long mod = 10_0000_0007l;

        long[][] translate = new long[][] {
            {24, 23, 23, 24, 24, 0, 0, 0, 0, 0},
            {1, 1, 1, 1, 0, 0, 0, 0, 0, 0},
            {1, 1, 1, 0, 1, 0, 0, 0, 0, 0},
            {0, 1, 0, 0, 0, 0, 0, 0, 0, 0},
            {0, 0, 1, 0, 0, 0, 0, 0, 0, 0},
            {0, 0, 0, 0, 0, 24, 23, 23, 24, 24},
            {0, 0, 0, 0, 0, 1, 1, 1, 1, 0},
            {0, 0, 0, 1, 0, 1, 1, 1, 1, 1},
            {0, 0, 0, 0, 0, 0, 1, 0, 0, 0},
            {0, 0, 0, 0, 0, 0, 0, 1, 0, 0},
        };

        Matrix matrix = new Matrix(translate);
        Matrix matrix2 = Matrix.quickPow(matrix, n, mod);

        Matrix vec = new Matrix(new long[][] {{1}, {0}, {0}, {0}, {0}, {0}, {0}, {0}, {0}, {0}});
        Matrix res = matrix2.mul(vec, mod);

        long ans = 0;
        for (int i = 5; i < 10; i++) {
            ans += res.arr[i][0];
            ans %= mod;
        }
        System.out.println(ans);
    }

    static 
    class Matrix {
        long[][] arr;
        int r, c;
        Matrix(long[][] arr) {
            this.arr = arr;
            this.r = arr.length;
            this.c = arr[0].length;
        }

        Matrix mul(Matrix other, long mod) {
            int nr = this.r, nc = other.c;
            long[][] res = new long[nr][nc];
            for (int i = 0; i < nr; i++) {
                for (int j = 0; j < nc; j++) {
                    long temp = 0;
                    for (int k = 0; k < c; k++) {
                        temp = (temp + arr[i][k] * other.arr[k][j] % mod) % mod;
                    }
                    res[i][j] = temp;
                }
            }
            return new Matrix(res);
        }

        static Matrix E(int n) {
            long[][] arr = new long[n][n];
            for (int i = 0; i < n; i++) {
                arr[i][i] = 1;
            }
            return new Matrix(arr);
        }

        static Matrix quickPow(Matrix base, long k, long mod) {
            Matrix r = Matrix.E(base.r);
            while (k > 0) {
                if (k % 2 == 1) {
                    r = r.mul(base, mod);
                }
                k /= 2;
                base = base.mul(base, mod);
            }
            return r;
        }
    }

}

---

F. 小红的零

整数末尾0的个数，取决于2和5的因子个数的最小值.

难点就在于：最小值

---

先来看2道基础题

对于一个数组arr， 给予一个x， 求${\sum }_{i=0}^{i=n?1}|arr[i]?x|$

这题的思路，就是对arr进行排序，然后绝对值去掉，这样就划分为2个部分，一部分小于x，另一部分大于等于x

利用前缀和预处理，可以二分到分界点， $O(log(n))$解决问题

求一个数组的所有子区间(2的因子个数)累加和

这是弱化版本，那其思路遍历右端点，然后累计

设S(i)为第i元素为右端点的所有区间的累加和

S(i) = S(i-1) + (i+1)*f(i)

最终S(i)的累加和 \sum S(i)

---

而这题的核心思路，其实上延续了类似思想

令f(x)为前x项的2因子的前缀和，
g(x)为前x项的5因子的前缀和

对于某个区间[l, r]

$贡献=min(f(r)?f(l?1),g(r)?g(l?1))$

令$z(x)=f(x)?g(x)$

则区间[l, r] 其贡献为

• $z(r)?z(l?1)\ge 0$

  • 贡献为 g? - g(l - 1)

• $z(r)?z(l?1)<0$

  • 贡献为f? - f(l - 1)

本质上这题的巧妙之处在于

• 维护2因子多的区间（累加和，个数）
• 维护5因子多的区间 (累加和，个数)

而这个因子多少，是一个变动的过程，根据右端点来决定范围

• 大于z(x)，为2因子多的区间

  $$n_x?f(x)?\sum _{y\in (z(y)>z(x))}f(y)$$

• 小于等于z(x), 则为5因子多的区间

  $$n_y?g(x)?\sum _{y\in (z(y)<=z(x))}g(y)$$

所以这边采用4个树状数组

fw2, fwc2代表2因子的前缀和f(x)，对应2因子的区间个数，

fw5, fwc5代表5因子的前缀和g(x)，对应5因子的区间个数

而把 z(x) 作为 树状数组的 index-key

因为2因子和5因子个数，最多30n，考虑到负值，最多60n

引入offset作为偏移，不需要离散化

感觉这题思路还是挺绕的，可能直接看代码，更容易理解

感觉这题掺杂了 前缀和的前缀和

import java.io.*;
import java.util.*;

public class Main {

    static class BIT {
        int n;
        long[] arr;
        public BIT(int n) {
            this.n = n;
            this.arr = new long[n + 1];
        }
        void update(int p, long v) {
            while (p <= n) {
                this.arr[p] += v;
                p += p&-p;
            }
        }
        long query(int p) {
            long res = 0;
            while (p > 0) {
                res += this.arr[p];
                p -= p&-p;
            }
            return res;
        }
    }

    static int split(int v, int b) {
        int cnt = 0;
        while (v % b == 0) {
            v /= b;
            cnt++;
        }
        return cnt;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int n = sc.nextInt();

        int mx = 60 * n; // 2^30 > 1e9, 因为绝对值的问题，所以30*2*n
        int offset = 30 * n; // 引入offset，是因为这边没有离散化，而是做了一个偏移，平衡负值

        BIT fw2 = new BIT(mx);  // 2的因子累加和
        BIT fwc2 = new BIT(mx); // 2的因子计数

        BIT fw5 = new BIT(mx);  // 5的因子累加和
        BIT fwc5 = new BIT(mx); // 5的因子计数

        long res = 0;
        int acc2 = 0, acc5 = 0;
        int diff = 0;
        for (int i = 0; i < n; i++) {
            // 前缀和为key
            fw2.update(diff + offset, acc2);
            fwc2.update(diff + offset, 1);
            fw5.update(diff + offset, acc5);
            fwc5.update(diff + offset, 1);

            int v = sc.nextInt();
            int n2 = split(v, 2);
            int n5 = split(v, 5);
            diff += (n2 - n5);
            acc2 += n2;
            acc5 += n5;

            // 进行统计计算
            long sum2 = fw2.query(mx) - fw2.query(diff + offset);
            long cnt2 = fwc2.query(mx) - fwc2.query(diff + offset);
            long sum5 = fw5.query(diff + offset);
            long cnt5 = fwc5.query(diff + offset);
            res += (acc2 * cnt2 - sum2) + (acc5 * cnt5 - sum5);
        }

        System.out.println(res);

    }

}

---

写在最后