数据在内存中的存储
整数在内存中的存储
整数的2进制表示方法有三种,即是原码,反码,补码。
三种表示方法均有符号位和数值位两个部分。
符号位“0”是正数,“1”是负数。一般放在最高位。剩余的都是数值位。
正整数的原码,反码,补码都相同。
负整数的三种表示方法各不相同。
下面画图解释:

对于整形的数据来说:数据存放内存中其实存放的是补码。
在计算机系统中,数值一律用补码来表示和存储。
原因在于,用补码,可以将符号位和数值位统一处理
同时,加法和减法也可以同一处理。此外,补码和与原码相互转换,不需要额外的硬件电路。
浮点数在内存中的存储
先看一个例子:

在这个代码中,num和*pFloat在内存中明明是一个数,为什么差别这么大?
下面就得介绍一下浮点数在计算机内部的表示方法。
根据国际标准,任意一个二进制浮点数V可以表示成下面的形式:
表示符号位,当S=0,V是正数;当S等于1的时候,V是负数。
- M表示有效数字,M是大于等于1,小于2的。
表示指数位。
举个例子:
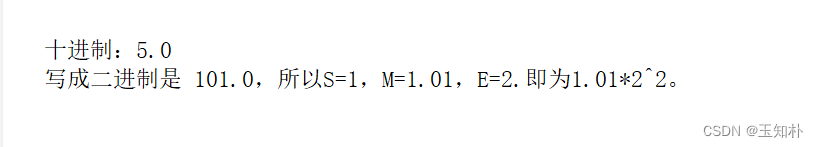
国际标准规定:
- 对于32位的浮点数,最高的一位存储符号S,接着的8位为存储指数E,剩下的23位存储有效数字M。
- 对于64位的浮点数,最高的一位存储符号S,接着的11位为存储指数E,剩下的52位存储有效数字M。
浮点数存的过程
国际标准对有效数字M和指数E,有一些特别规定。
前面说过,M是大于等于1并且小于2时,M可以写成1.xxx的形式,其中xxx表示小数部分。
国际标准规定,在计算机内部保存M的时候,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxx部分。这样做的目的是,是节省1位有效数字。
指数E是无符号整数。
这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是我们知道,科学计数法中的E是可能出现负数的,所以规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数127;对于11位的E,这个中间数1023.
浮点数取的过程
指数E从内存中取出还可以再分成三种情况:
E不全为0不全为1
这个时候,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023)。得到真实值,再将有效数字M前加上第一位的1。
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第一位的1,而是还原为0.xxxx的小数。这样做是为了表示+-0,以及接近于0的很小的数字。
E全为1
这时,如果有效数字M全为0,表示+-无穷大(政府取决于符号位)。
总结
让我们回到一开始的题目:
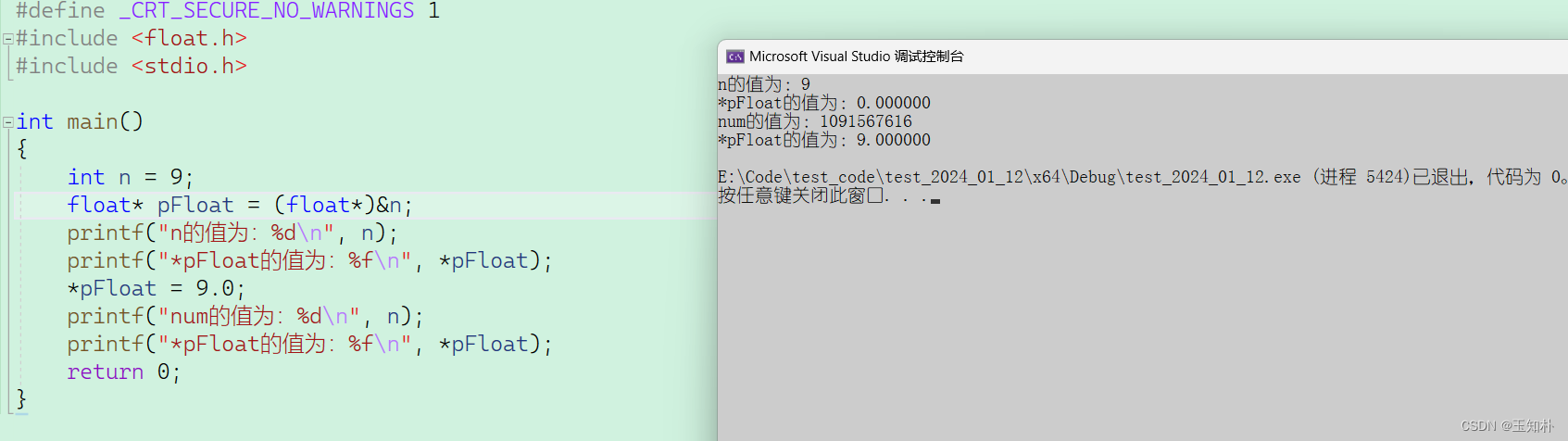
先看第一个环节,为什么9还原成浮点数,就成了0.000000

首先,将9的二进制序列按照浮点数的形式拆分,得到S=0,E=00000000。
最后M=000 0000 0000 0000 0000 1001.
所以浮点数V=(-1)^0*00000000000000000001001*2^(-126)=1.001*2^(-146)
显然,V是一个很小的接近于0的正数,所以用十进制小数表示就是0.000000
再看第二个环节,浮点数9.0,为什么打印成1091567616
首先,浮点数9.0等于二进制1001.0,换算成科学计数法是:1.001*2^3
所以,第一位的符号位S=0,有效数字M等于001后面再加上20个0,凑满23位,指数E等于3+127=130,即10000010
所以写成二进制形式,应该是S+E+M,即是0 10000010 001 0000 0000 0000 0000 0000。
这个32位的二进制数,被当做整数来解析的时候,就是整数在内存中的补码,原码正是1091567616。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 自然语言处理-用于预训练词嵌入的数据集
- Python高级用法:property
- 2023读书笔记55|微读699元的书读后感——《走进美加风光摄影集》
- 51单片机介绍
- @RestController和@Controller区别
- 世微AP8851 DC-DC降压恒压芯片 2.5A应用资料及BOM清单
- 前缀和算法 -- [模版]一维前缀和
- 【信号与系统】【北京航空航天大学】实验三、连续时间信号的频域分析 【MATLAB】
- JavaScript:Date 对象-时间日期
- Python容器类公共操作