《二叉树》——1

目录

前言：

二叉树的链式结构

二叉树的遍历

前序遍历：

中序遍历：

后序遍历：

总结：

---

前言：

从本文开始，将进一步深入学习编程语言思想，从二叉树开始我们将接触许许多多的递归算法以及思想，我们应当重思想而再看代码，切记不可颠倒。相信大家在之后的学习或多或少会遇到些许困难，那么在刚开始学习递归算法时，我们需要勤动手，多画画图来帮助我们更好的理解递归。

接下来我们先来简单了解下二叉树的链式结构

二叉树的链式结构

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}TreeNode;

TreeNode* BuyTreeNode(int x)
{
	TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
	if (root == NULL)
	{
		perror("BuyTreeNode -> malloc");
		exit(-1);
	}
	root->data = x;
	root->right = root->left = NULL;
	return root;
}

TreeNode* CreateTree()
{
	TreeNode* a = BuyTreeNode(1);
	TreeNode* b = BuyTreeNode(2);
	TreeNode* c = BuyTreeNode(3);
	TreeNode* d = BuyTreeNode(4);
	TreeNode* e = BuyTreeNode(5);
	TreeNode* f = BuyTreeNode(6);
	a->left = b;
	a->right = d;

	b->left = c;
	
	d->left = e;
	d->right = f;
	return a;
}

注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。

通过上述的代码，不难得出，这颗新创建的二叉树如图：

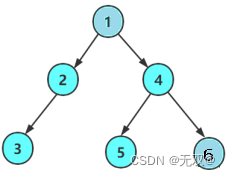
通过之前的回顾，我们知道二叉树是：

1、空树

2、非空：根节点，根节点的左子树、根节点的右子树组成的。

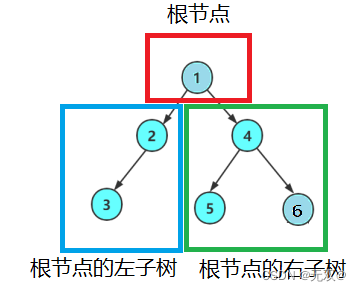
从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。

二叉树的遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

按照规则，二叉树的遍历有前序/中序/后序的递归结构遍历：
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
?

前序遍历：

void PrevOrder(TreeNode* root)//前序排序
{
	if (root == NULL)
	{
		printf("N ");
	}
	else
	{
		printf("%d ", root->data);
		PrevOrder(root->left);
		PrevOrder(root->right);
	}
}

前序遍历简单的来说，就是先访问根节点，再访问左节点，最后访问右节点。

我们可以简化为（根、左、右）

那么通过以下的图片就能较好的解释这一遍历。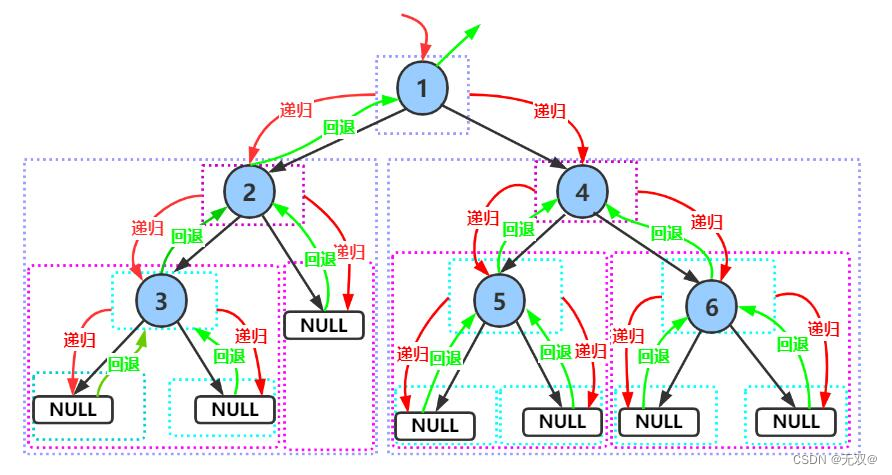

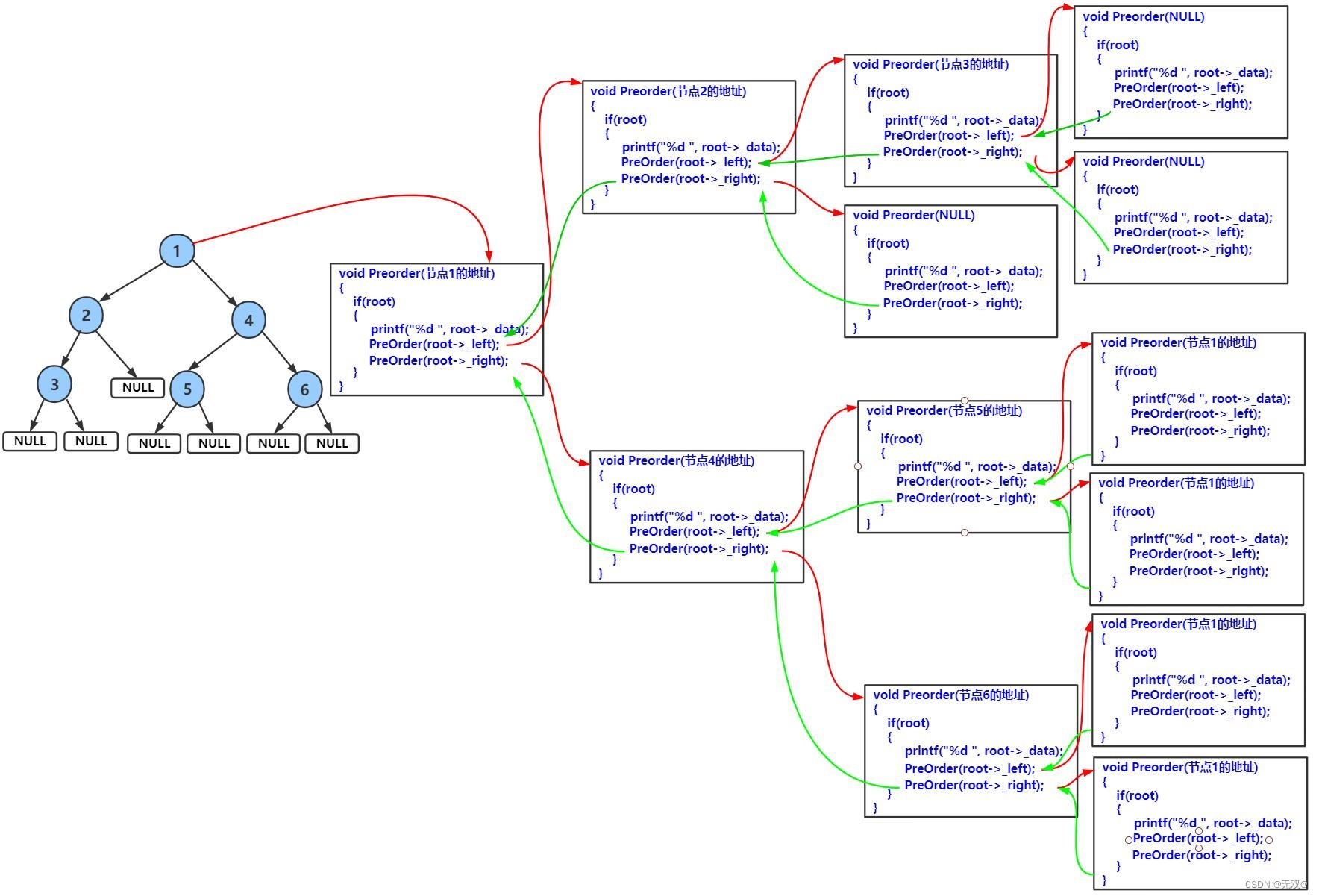
中序遍历：

那么对于中序遍历，就是遵从（左、根、右）

void InOrder(TreeNode* root)//中序遍历
{
	if (root == NULL)
	{
		printf("N ");
	}
	else
	{
		InOrder(root->left);
		printf("%d ", root->data);
		InOrder(root->right);
	}
}

后序遍历：

那么对于后序遍历，就是遵从（左、右、根）

void AfterOrder(TreeNode* root)//后序排序
{
	if (root == NULL)
	{
		printf("N ");
	}
	else
	{
		AfterOrder(root->left);
		AfterOrder(root->right);
		printf("%d ", root->data);
	}
}

总结：

先序遍历:1 2 3 N N N 4 5 N N 6 N N

中序遍历:N 3 N 2 N 1 N 5 N 4 N 6 N

后序遍历:N N 3 N 2 N N 5 N N 6 4 1

?