day27 组合总和 组合总和Ⅱ 分割回文串

题目1：39 组合总和

题目链接：39 组合总和

题意

找出无重复元素的正整数数组candidates中元素和为目标数target的所有不同组合，同一个数字可重复选取

回溯

回溯三部曲：

1）参数和返回值

2）终止条件

3）单层搜索逻辑

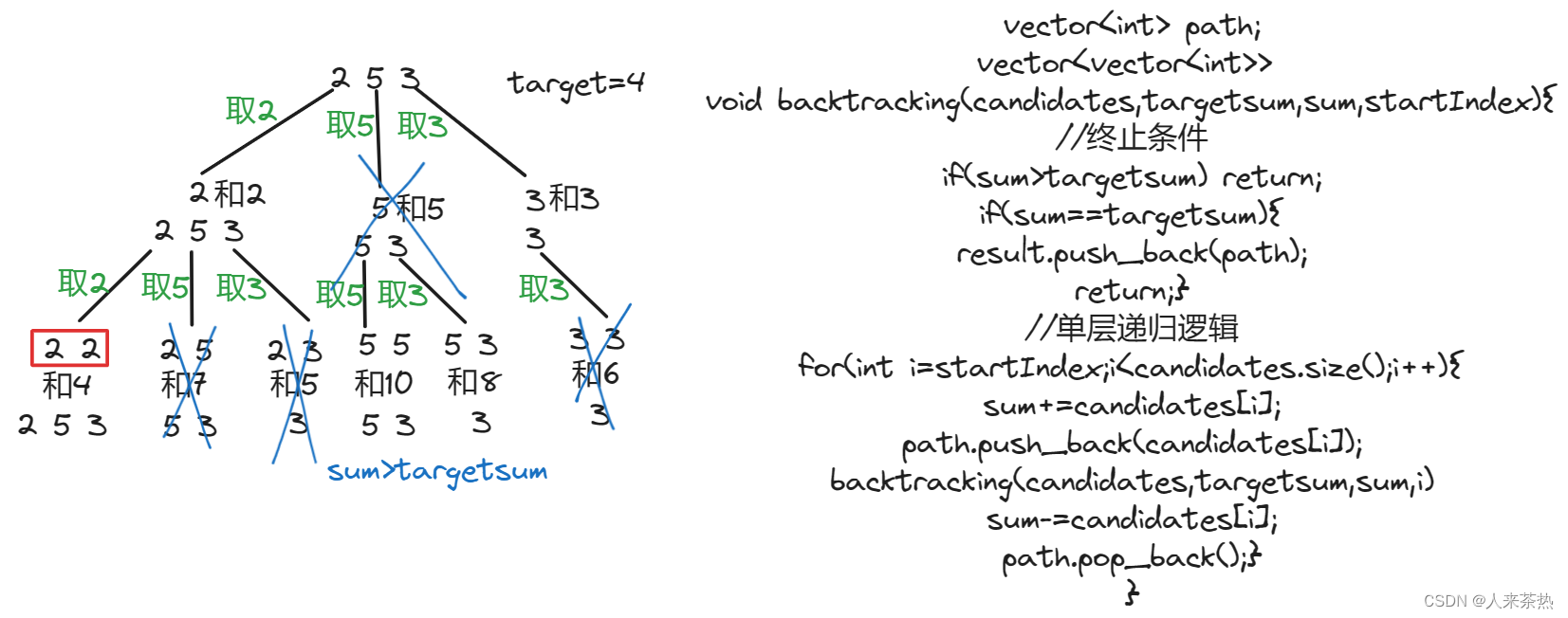
代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& candidates,int targetsum,int sum,int startIndex){
        if(sum>targetsum) return;
        //终止条件
        if(sum==targetsum){
            result.push_back(path);
            return;
        }
        //单层递归逻辑
        for(int i=startIndex;i<candidates.size();i++){
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates,targetsum,sum,i);//递归
            sum -= candidates[i];//回溯
            path.pop_back();//回溯
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtracking(candidates,target,0,0);
        return result;
    }
};

剪枝

给数组递增排序，排序后，如果组合中的一个分支使得和（sum+candidates[i]）大于targetsum，那么该分支及其后面的分支没有必要存在了，因为和肯定都大于target了

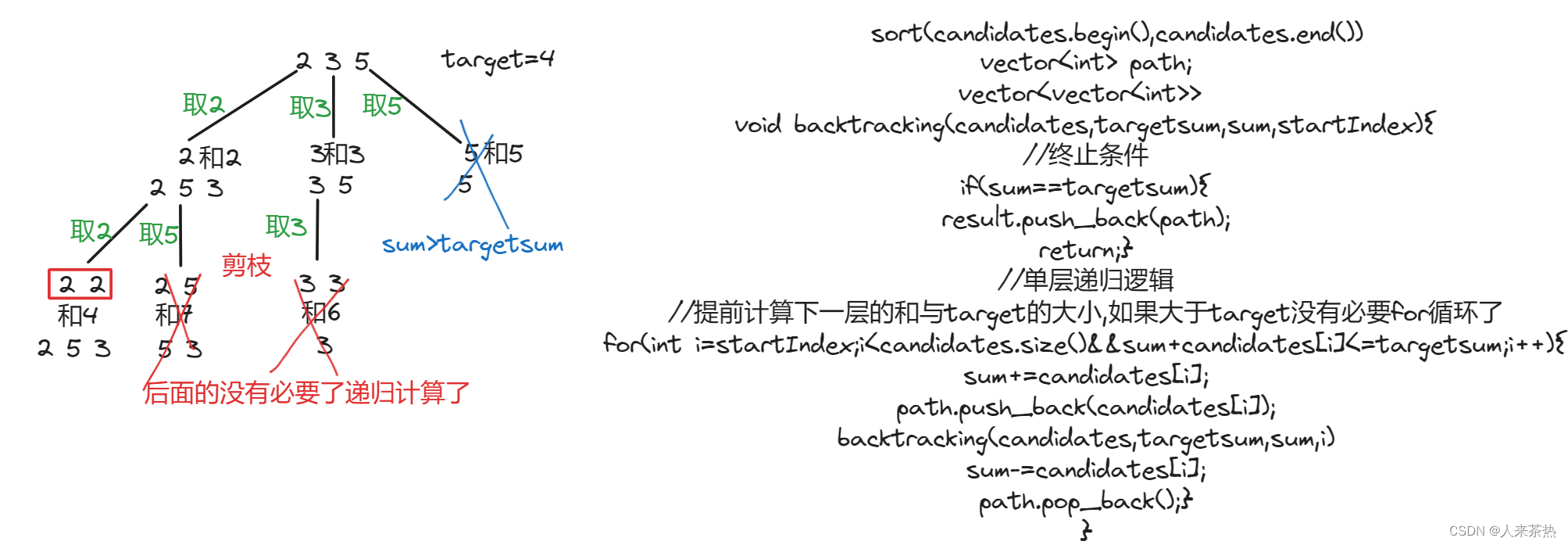
代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& candidates,int targetsum,int sum,int startIndex){
        //终止条件
        if(sum==targetsum){
            result.push_back(path);
            return;
        }
        //单层递归逻辑
        //注意限制条件是<= 一定要包含等于，因为还要将candidates[i]放入path数组中
        for(int i=startIndex;i<candidates.size()&&sum+candidates[i]<=targetsum;i++){
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates,targetsum,sum,i);//递归
            sum -= candidates[i];//回溯
            path.pop_back();//回溯
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        //排序
        sort(candidates.begin(),candidates.end());
        backtracking(candidates,target,0,0);
        return result;
    }
};

• 时间复杂度: O(n * 2^n)，复杂度的上界，剪枝使得真实的时间复杂度小于该值
• 空间复杂度: O(target)

题目2：组合总和Ⅱ

题目链接：40 组合总和Ⅱ

题意

找出正整数数组candidates中使得元素和为target的组合，组合不能重复，数组中每个元素只能使用1次，但是candidates中可能存在重复的元素 例如 [2,2,2] target=4 只有1个组合满足[2 2]要求

回溯

回溯三部曲：

1）参数和返回值

2）终止条件

3）单层递归逻辑

本题主要是包含去重的操作? 将数组按照增序排列，将相同的元素放在紧邻的位置

代码

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& candidates,int targetsum,int sum,int startIndex,vector<bool>& used){
        //终止条件
        if(sum>targetsum) return;
        if(sum==targetsum){
            result.push_back(path);
            return;
        }
        //单层递归逻辑
        for(int i=startIndex;i<candidates.size();i++){
            //树层去重
            if(i>0 && candidates[i]==candidates[i-1] && used[i-1]==0) continue;
            sum += candidates[i];
            path.push_back(candidates[i]);
            used[i] = true;
            backtracking(candidates,targetsum,sum,i+1,used);//递归
            sum -= candidates[i];//回溯
            path.pop_back();//回溯
            used[i] = false;//回溯
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        //对数组进行排序，使得数组中数值相等的元素可以相邻在一起，这样方便去重
        sort(candidates.begin(),candidates.end());
        vector<bool> used(candidates.size(),false); 
        backtracking(candidates,target,0,0,used);
        return result;
    }
};

剪枝

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& candidates,int targetsum,int sum,int startIndex,vector<bool>& used){
        //终止条件
        if(sum==targetsum){
            result.push_back(path);
            return;
        }
        //单层递归逻辑
        for(int i=startIndex;i<candidates.size()&&sum+candidates[i]<=targetsum;i++){
            //树层去重
            if(i>0 && candidates[i]==candidates[i-1] && used[i-1]==0) continue;
            sum += candidates[i];
            path.push_back(candidates[i]);
            used[i] = true;
            backtracking(candidates,targetsum,sum,i+1,used);//递归
            sum -= candidates[i];//回溯
            path.pop_back();//回溯
            used[i] = false;//回溯
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        //对数组进行排序，使得数组中数值相等的元素可以相邻在一起，这样方便去重
        sort(candidates.begin(),candidates.end());
        vector<bool> used(candidates.size(),false); 
        backtracking(candidates,target,0,0,used);
        return result;
    }
};

• 时间复杂度: O(n * 2^n)
• 空间复杂度: O(n)

题目3：131 分割回文串

题目链接：131 分割回文串

题意

将字符串s（仅由小写字母组成）分割成若干回文子串? 回文串是正读和反读相同的子串,返回分割方案

回溯

回溯三部曲：

1）参数和返回值

2）终止条件

3）单层搜索逻辑

代码

class Solution {
public:
    //判断字符串是否是回文串
    bool ispalidrom(const string& s,int start,int end){
        for(int i=start,j=end;i<j;i++,j--){
            if(s[i]!=s[j]) return false;
        }
        return true;
    }
    vector<string> path;//存放单个分割结果
    vector<vector<string>> result;//存放所有分割方案
    void backtracking(const string& s,int startIndex){
        //终止条件
        if(startIndex==s.size()){
            result.push_back(path);//path中只存放是回文串的子串
            return;
        }
        //单层搜索逻辑
        for(int i=startIndex;i<s.size();i++){
            if(ispalidrom(s,startIndex,i)){
                //截取[statrIndex,i]的子串
                string str  = s.substr(startIndex,i-startIndex+1);
                path.push_back(str);
            }
            else continue;
            backtracking(s,i+1);//递归
            path.pop_back();//回溯
        }
    }
    vector<vector<string>> partition(string s) {
        backtracking(s,0);
        return result;
    }
};

• 时间复杂度: O(n * 2^n)
• 空间复杂度: O(n^2)