计算智能 | 蚁群算法——旅行商问题(TSP)python
发布时间:2023年12月18日
目录
一、求解TSP(city31)问题的python代码?
import numpy as np
import random
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
class ACA_TSP:
def __init__(self,n,X,Y,m,N,Q,P,alpha,beta):
'''
:param n: 城市数量
:param X: 城市的横坐标
:param Y: 城市的纵坐标
:param m: 蚁群规模
:param N: 最大迭代步数
:param Q: 蚂蚁循环一周或一个过程在经过的路径上所释放的信息素总量
:param P: 信息素挥发系数
:param alpha: 信息启发式因子
:param beta: 期望启发式因子
'''
self.n=n
self.X=X
self.Y=Y
self.m=m
self.N=N
self.Q=Q
self.P=P
self.alpha=alpha
self.beta=beta
def distance(self):
'''
return: 所有城市之间的距离矩阵
'''
D=np.zeros((self.n,self.n))
for i in range(self.n):
for j in range(self.n):
D[i][j]=np.sqrt((self.X[i]-self.X[j])**2+(self.Y[i]-self.Y[j])**2)
return D
def initial_X(self):
#随机生成初始路径
X0=random.sample(range(self.n),self.n)
return X0
def initial_tao(self,X0,D):
'''
:param X0: 初始路径
:param D: 距离矩阵
:return: 初始信息素浓度
'''
#计算初始路径长度
S=0
for i in range(self.n):
if i!=self.n-1:
S=S+D[X0[i]][X0[i+1]]
else:
S=S+D[X0[i]][X0[0]]
#计算初始信息素浓度
tao_00=self.m/S
tao_0=np.zeros((self.n,self.n))
tao_0=tao_0+tao_00
return tao_0
def initial_city(self):
#为每只蚂蚁随机选择出发城市
initial=[random.randint(0,self.n-1) for i in range(self.m)]
return initial
'''一只蚂蚁在一次周期内选择路径的过程'''
def seek(self,initial,tao,D):
'''
:param initial: 蚂蚁出发的城市序号
:param tao: 信息素浓度矩阵
:param D: 距离矩阵
:return: 蚂蚁最终选择的路径
'''
#存储已经遍历的城市
ls=[]
ls.append(initial)
for i in range(self.n-1):
#蚂蚁未经过的城市序号
l=[]
for j in range(self.n):
if j not in ls:
l.append(j)
if len(l)==1:
ls.append(l[-1])
else:
#计算蚂蚁下一次访问某个城市的概率
ratio_l0=[]
for j in range(len(l)):
r=(tao[ls[-1]][l[j]]**self.alpha)*((1/D[ls[-1]][l[j]])**self.beta)
ratio_l0.append(r)
#得到概率
ratio_l=[ratio_l0[j]/sum(ratio_l0) for j in range(len(ratio_l0))]
#计算累计概率
ratio_cum=[0]
for j in range(len(ratio_l)):
cum=ratio_cum[-1]+ratio_l[j]
ratio_cum.append(cum)
#用轮盘赌选择算法选择下一个访问城市
q=random.uniform(0,1)
for j in range(1,len(ratio_cum)):
if q>=ratio_cum[j-1] and q<ratio_cum[j]:
ls.append(l[j-1])
#返回最终选择的路径
return ls
'''信息素浓度增量(使用蚁周模型)'''
def add_tao(self,ls,D):
'''
:param ls: 蚂蚁选择的路径
:param D: 距离矩阵
:return: 信息素增量
'''
#计算路径长度
s=0
for i in range(self.n):
if i!=self.n-1:
s=s+D[ls[i]][ls[i+1]]
else:
s=s+D[ls[i]][ls[0]]
#初始化信息素增量
add=np.zeros((self.n,self.n))
for i in range(self.n):
if i!=self.n-1:
add[ls[i]][ls[i+1]]+=self.Q/s
add[ls[i+1]][ls[i]]+=self.Q/s
else:
add[ls[i]][ls[0]]+=self.Q/s
add[ls[0]][ls[i]]+=self.Q/s
return add
'''使用蚁群算法求解旅行商问题'''
def TSP(self):
#得到初始路径
initial_X0=ACA_TSP.initial_X(self)
#各个城市之间的距离矩阵
D=ACA_TSP.distance(self)
#初始信息素浓度矩阵
tao_0=ACA_TSP.initial_tao(self,initial_X0,D)
#存储历史最优路径
best_X=[]
#存储历史最短距离
best_S=[]
for i in range(self.N):
#为每只蚂蚁随机选择出发的城市
initial_city=ACA_TSP.initial_city(self)
#存储每只蚂蚁最后选择的路径
X=[]
#存储每只蚂蚁最后选择的路径的长度
S=[]
#初始化信息素浓度增量
add=np.zeros((self.n,self.n))
for j in range(self.m):
#选择路径
X_choose=ACA_TSP.seek(self,initial_city[j],tao_0,D)
X.append(X_choose)
#选择的路径长度
s=0
for k in range(self.n):
if k!=self.n-1:
s=s+D[X_choose[k]][X_choose[k+1]]
else:
s=s+D[X_choose[k]][X_choose[0]]
S.append(s)
#计算信息素浓度增量
add_tao=ACA_TSP.add_tao(self,X_choose,D)
add=add+add_tao
#得到所有蚂蚁的最短距离
best_S0=min(S)
#得到所有蚂蚁的最优路径
best_X0=X[np.argmin(S)]
if len(best_X)==0:
best_X.append(best_X0)
best_S.append(best_S0)
else:
if best_S0<best_S[-1]:
best_X.append(best_X0)
best_S.append(best_S0)
else:
best_X.append(best_X[-1])
best_S.append(best_S[-1])
#更新信息素浓度
tao_0=tao_0*(1-self.P)+add_tao
#绘制优化过程
fig=plt.figure(facecolor="snow")
plt.plot(range(self.N),best_S,color="tomato",label='最短距离')
plt.legend()
plt.grid()
plt.xlabel("代数")
plt.ylabel("最短距离")
plt.title("蚁群算法——TSP的优化过程")
#绘制最优路径图
path=best_X[-1] #最优路径
fig=plt.figure(facecolor="snow")
plt.scatter(self.X,self.Y,color="red")
for i in range(self.n):
if i!=self.n-1:
plt.plot([self.X[path[i]],self.X[path[i+1]]],[self.Y[path[i]],self.Y[path[i+1]]],color="plum")
else:
plt.plot([self.X[path[i]],self.X[path[0]]],[self.Y[path[i]],self.Y[path[0]]],color="plum")
plt.xlabel("X")
plt.ylabel("Y")
plt.title("最优路径图")
plt.show()
#返回最优路径和最短距离
return best_X[-1],best_S[-1]
'''主函数'''
if __name__=="__main__":
'''城市的数量'''
n=31
'''定义31个城市的坐标'''
city_x=[1304,3639,4177,3712,3488,3326,3238,4196,4312,4386,3007,2562,2788,
2381,1332,3715,3918,4061,3780,3676,4029,4263,3429,3507,3394,3439,
2935,3140,2545,2778,2370]
city_y=[2312,1315,2244,1399,1535,1556,1229,1044,790,570,1970,1756,1491,
1676,695,1678,2179,2370,2212,2578,2838,2931,1908,2376,2643,3201,
3240,3550,2357,2826,2975]
'''蚁群规模'''
m=21
'''最大迭代步数'''
N=300
'''蚂蚁循环一周或一个过程在经过的路径上所释放的信息素总量'''
Q=20
'''信息素挥发系数'''
P=0.5
'''信息启发式因子'''
alpha=1
'''期望启发式因子'''
beta=3
'''创建一个对象'''
Tsp=ACA_TSP(n,city_x,city_y,m,N,Q,P,alpha,beta)
best_X,best_S=Tsp.TSP()
print("最短路径:\n{}".format(best_X))
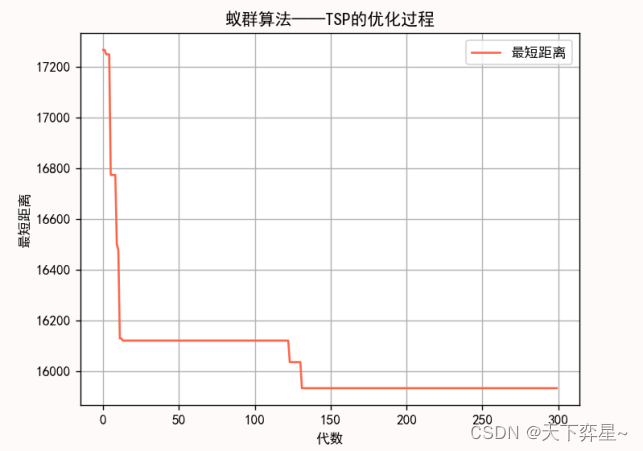
print("最短距离:\n{}".format(best_S))二、python运行结果
当蚁群规模m=21,最大迭代步数N=300,蚂蚁循环一周或一个过程在经过的路径上所释放的信息素总量Q=20,信息素挥发系数,信息启发式因子
,期望启发式因子
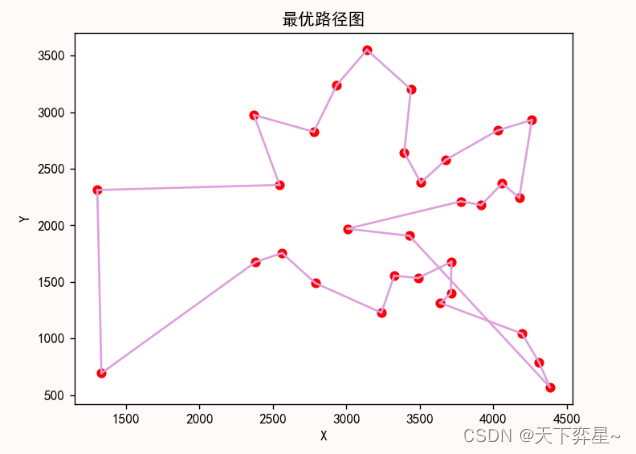
,程序运行结果如下:

?
?
文章来源:https://blog.csdn.net/m0_70452407/article/details/135061070
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!