概率论与数理统计————1.随机事件与概率

发布时间：2024年01月15日

一、随机事件

随机试验：满足三个特点

（1）可重复性：可在相同的条件下重复进行

（2）可预知性：每次试验的可能不止一个，事先知道试验的所有可能结果

（3）不确定性：每次试验不能确定实验结果

随机试验记作E

样本空间：随机试验E的所有可能的结果构成的集合

样本点：样本空间的每个元素是一个样本点

随机事件：样本空间的子集为一个随机事件（事件放生：该事件的某个样本点出现）

必然事件：必然发生的事件

不可能事件：不可能发生的事件

二、事件间的关系和运算

1、包含

A $\subset$ B：事件A发生，则事件B必发生

A=B????? $< = >$ ??? $A\subset B$ 且 $B\subset A$

2.事件的和（并）

A $\cup$ B 或A+B :? 事件A和事件B至少发生一个

3、事件的积（交）

AB或A $\cap$ B :? 事件A和事件B同时发生

4、事件的差

A-B：事件A发生了，事件B不发生

重要公式：A-B=A-AB

5、互不相容事件

A和B互斥则A和B没有交集

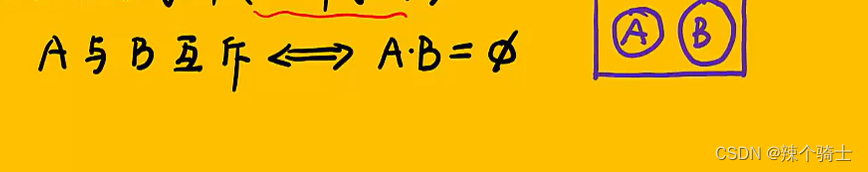
6、对立事件

交换律： $A\cup B=B\cup A,A\cap B=B\cap A$

结合律： $(A\cup B)\cup C,A\cup (B\cup C)$ ? , ?????? $A\cap B\cap C=A\cap (B\cap C)$

分配律： $(A\cup B)\cap C=(A\cap C)\cup (B\cap C )$

???????????? $(A\cap B)\cup C=(A\cup C)\cap (B\cup C)$

德摩根律：

三、概率的定义和性质

设一个随机试验，重复做n次，A为随机事件，发生m次则

$\frac{m}{n}$ =p为A发生的频率，当试验次数足够大时，p为事件A发生的概率

非负性：0 $\leq p\leq 1$

规范性：P（s）=1；p（ $\o$ $\O$ $\not{o}$ ）=0

有限可加性：若A,B互斥，则p（A $\cup$ B）=P（A）+P（B）

互补性：P（ $\bar{A}$ ）=1-P(A)

减法公式：p（A-B）=p（A）-p（AB）

加法公式：p（ $A\cup B$ ）=p（A）+p（B）-p（AB）

文章来源:https://blog.csdn.net/2201_75333727/article/details/135589554
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

最新文章