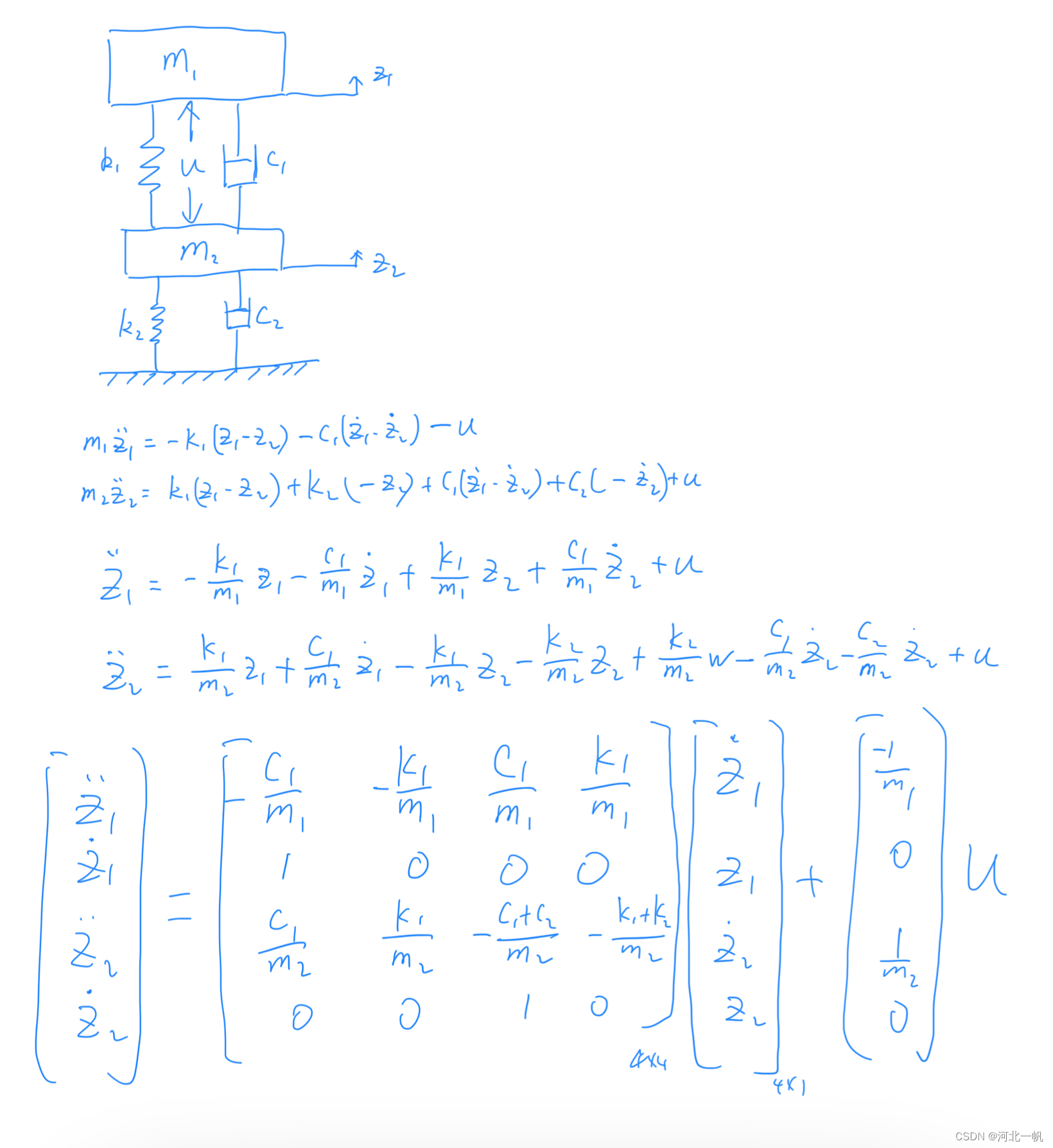
二自由度弹簧阻尼模型LQR控制

import numpy as np
from scipy.integrate import odeint
from scipy.linalg import solve_continuous_are
import matplotlib.pyplot as plt


m1 = 1.0
m2 = 2.0
k1 = 3.0
k2 = 4.0
c1 = 0.5
c2 = 0.7

A = np.array([[-c1/m1, -k1/m1, c1/m1, k1/m1],
              [1, 0, 0, 0],
              [c1/m2, k1/m2, -1*(c1+c2)/m2, -1*(k1+k2)/m2],
              [0, 0, 1, 0]])

B = np.array([[-1/m1],
              [0],
              [1/m2],
              [0]])
Q = np.eye(4) * 1
R = 1

P = solve_continuous_are(A, B, Q, R)
print(P)
K = 1/R * B.T @ P
print(K)


def func_no_control(x, t):
    return A @ x

def func_with_control(x, t):
    return A @ x + B @ -K @ x


x0 = [0.0, 0.0, 2.0, 1.0]

t_max = 60
dt = 0.01
t = np.linspace(0, t_max, int(t_max/dt))

x_no_control = odeint(func_no_control, x0, t)
x_with_control = odeint(func_with_control, x0, t)

plt.figure(figsize=(10, 6))
plt.plot(t, x_no_control[:, 1], label='z1 no control')
plt.plot(t, x_with_control[:, 1], label='z1 with control')
plt.xlabel('Time')
plt.ylabel('Displacement')
plt.title('Displacement vs Time')
plt.legend()
plt.grid(True)
plt.show()

?