三角函数诱导公式

发布时间：2023年12月24日

推导原理

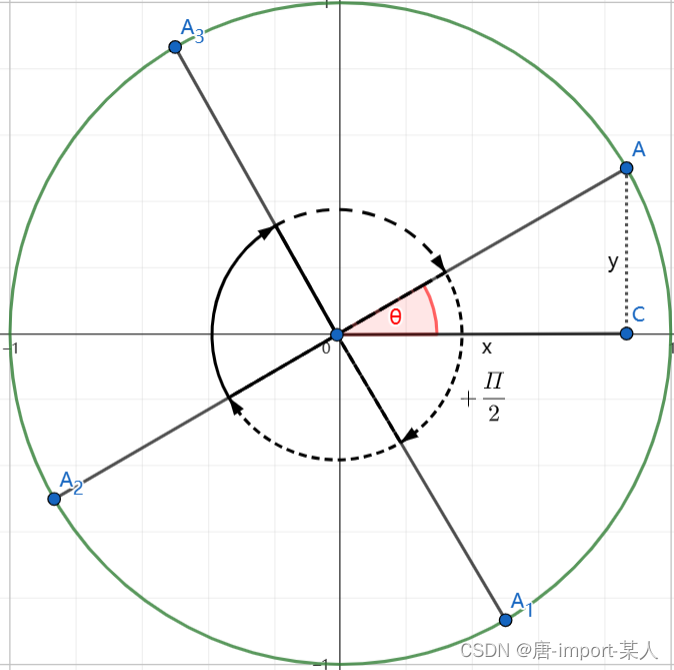
①三角形内角和180°
②y值是线段OA投影到周的移动距离,即AC⊥x
③平面几何中的坐标正负
在这里插入图片描述

1. 2 k Π 2kΠ 2kΠ

线移动2k+θ后

  • 线与x的夹角未发生变化
  • 投影x轴位置未变化
  • 投影y轴位置未变化
    s i n ( 2 k + θ ) = s i n ( θ ) , k ∈ Z sin(2k+θ)=sin(θ),k∈Z sin(2k+θ)=sin(θ),k∈Z
    c o s ( 2 k + θ ) = c o s ( θ ) , k ∈ Z cos(2k+θ)=cos(θ),k∈Z cos(2k+θ)=cos(θ),k∈Z
    t a n ( 2 k + θ ) = t a n ( θ ) , k ∈ Z tan(2k+θ)=tan(θ),k∈Z tan(2k+θ)=tan(θ),k∈Z
    c o t ( 2 k + θ ) = c o t ( θ ) , k ∈ Z cot(2k+θ)=cot(θ),k∈Z cot(2k+θ)=cot(θ),k∈Z

2. 2 k Π + Π 2 2kΠ+\frac{Π}{2} 2kΠ+2Π?

线移动 2 k Π + Π 2 + θ 2kΠ+\frac{Π}{2}+θ 2kΠ+2Π?+θ后

  • 线与x轴夹角变换,即 Π 2 ? θ \frac{Π}{2}-θ 2Π??θ
  • 投影到x的+轴
  • 投影y的-轴
    s i n ( Π 2 + θ ) = c o s ( θ ) , k ∈ Z sin(\frac{Π}{2}+θ)=cos(θ),k∈Z sin(2Π?+θ)=cos(θ),k∈Z
    c o s ( Π 2 + θ ) = s i n ( θ ) , k ∈ Z cos(\frac{Π}{2}+θ)=sin(θ),k∈Z cos(2Π?+θ)=sin(θ),k∈Z
    t a n ( Π 2 + θ ) = c o t ( θ ) , k ∈ Z tan(\frac{Π}{2}+θ)=cot(θ),k∈Z tan(2Π?+θ)=cot(θ),k∈Z
    t a n ( Π 2 + θ ) = t a n ( θ ) , k ∈ Z tan(\frac{Π}{2}+θ)=tan(θ),k∈Z tan(2Π?+θ)=tan(θ),k∈Z

3. 2 k Π + Π 2kΠ+Π 2kΠ+Π

线移动 2 k Π + Π 2kΠ+Π 2kΠ+Π后

  • 线与x轴发生夹角未发生变换
  • 投影x的-轴
  • 投影y的-轴
    s i n ( 2 k Π + Π + θ ) = s i n ( θ ) , k ∈ Z sin(2kΠ+Π+θ)=sin(θ),k∈Z sin(2kΠ+Π+θ)=sin(θ),k∈Z
    c o s ( 2 k Π + Π + θ ) = ? c o s ( θ ) , k ∈ Z cos(2kΠ+Π+θ)=-cos(θ),k∈Z cos(2kΠ+Π+θ)=?cos(θ),k∈Z
    t a n ( 2 k Π + Π + θ ) = ? t a n ( θ ) , k ∈ Z tan(2kΠ+Π+θ)=-tan(θ),k∈Z tan(2kΠ+Π+θ)=?tan(θ),k∈Z
    c o t ( 2 k Π + Π + θ ) = ? c o t ( θ ) , k ∈ Z cot(2kΠ+Π+θ)=-cot(θ),k∈Z cot(2kΠ+Π+θ)=?cot(θ),k∈Z

4. 2 k Π + 3 Π 2 2kΠ+\frac{3Π}{2} 2kΠ+23Π?

线移动 2 k Π + 3 Π 2 2kΠ+\frac{3Π}{2} 2kΠ+23Π?后

  • 线与x轴发生夹角未生变换,即 Π 2 ? θ \frac{Π}{2}-θ 2Π??θ
  • 投影x的-轴
  • 投影y的+轴
    s i n ( 2 k Π + 3 Π 2 + θ ) = ? c o s ( θ ) , k ∈ Z sin(2kΠ+\frac{3Π}{2}+θ)=-cos(θ),k∈Z sin(2kΠ+23Π?+θ)=?cos(θ),k∈Z
    c o s ( 2 k Π + 3 Π 2 + θ ) = s i n ( θ ) , k ∈ Z cos(2kΠ+\frac{3Π}{2}+θ)=sin(θ),k∈Z cos(2kΠ+23Π?+θ)=sin(θ),k∈Z
    t a n ( 2 k Π + 3 Π 2 + θ ) = ? c o t ( θ ) , k ∈ Z tan(2kΠ+\frac{3Π}{2}+θ)=-cot(θ),k∈Z tan(2kΠ+23Π?+θ)=?cot(θ),k∈Z
    c o t ( 2 k Π + 3 Π 2 + θ ) = ? t a n ( θ ) , k ∈ Z cot(2kΠ+\frac{3Π}{2}+θ)=-tan(θ),k∈Z cot(2kΠ+23Π?+θ)=?tan(θ),k∈Z

5.-θ

-θ表示线移动角度由正方向变换正方向移动
s i n ( ? θ ) = ? s i n ( θ ) sin(-θ)=-sin(θ) sin(?θ)=?sin(θ)
c o s ( ? θ ) = c o s ( θ ) cos(-θ)=cos(θ) cos(?θ)=cos(θ)
t a n ( ? θ ) = ? t a n ( θ ) tan(-θ)=-tan(θ) tan(?θ)=?tan(θ)
c o t ( ? θ ) = ? c o t ( θ ) cot(-θ)=-cot(θ) cot(?θ)=?cot(θ)

文章来源:https://blog.csdn.net/tyh751734196/article/details/135186332
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章