证明四元数乘法与旋转矩阵乘法等价
刚体四元数姿态控制 一文中没有证明的公式
R
(
Q
1
)
R
(
Q
2
)
=
R
(
Q
1
°
Q
2
)
R(Q_1)R(Q_2)=R(Q_1\circ Q_2)
R(Q1?)R(Q2?)=R(Q1?°Q2?)
在这篇文章中使用 sympy 证明。
相关公式
四元数分成标量和向量两个部分
Q
=
[
s
,
v
?
]
Q=[s,\vec v]
Q=[s,v]
四元数转旋转矩阵
R
(
Q
)
=
(
s
2
?
v
?
T
v
?
)
I
+
2
v
?
v
?
T
+
2
s
v
?
∧
=
[
q
0
2
+
q
1
2
?
q
2
2
?
q
3
2
2
q
1
q
2
?
2
q
0
q
3
2
q
1
q
3
+
2
q
0
q
2
2
q
1
q
2
+
2
q
0
q
3
q
0
2
?
q
1
2
+
q
2
2
?
q
3
2
2
q
2
q
3
?
2
q
0
q
1
2
q
1
q
3
?
2
q
0
q
2
2
q
2
q
3
+
2
q
0
q
1
q
0
2
?
q
1
2
?
q
2
2
+
q
3
2
]
\begin{aligned} R(Q) =& (s^2-\vec v^\text{T}\vec v)I+2\vec v\vec v^\text{T}+2s\vec v^{\wedge}\\ =& \begin{bmatrix} q_0^2+q_1^2-q_2^2-q_3^2 & 2q_1q_2-2q_0q_3 & 2q_1q_3+2q_0q_2 \\ 2q_1q_2+2q_0q_3 & q_0^2-q_1^2+q_2^2-q_3^2 & 2q_2q_3-2q_0q_1 \\ 2q_1q_3-2q_0q_2 & 2q_2q_3+2q_0q_1 & q_0^2-q_1^2-q_2^2+q_3^2 \end{bmatrix} \\ \end{aligned}
R(Q)==?(s2?vTv)I+2vvT+2sv∧
?q02?+q12??q22??q32?2q1?q2?+2q0?q3?2q1?q3??2q0?q2??2q1?q2??2q0?q3?q02??q12?+q22??q32?2q2?q3?+2q0?q1??2q1?q3?+2q0?q2?2q2?q3??2q0?q1?q02??q12??q22?+q32??
??
四元数乘法
Q
1
°
Q
2
=
[
s
1
,
v
?
1
]
°
[
s
2
,
v
?
2
]
=
[
s
1
s
2
?
v
?
1
?
v
?
2
,
s
1
v
?
2
+
s
2
v
?
1
+
v
?
1
×
v
?
2
]
Q_1\circ Q_2=[s_1,\vec v_1]\circ[s_2,\vec v_2] =[s_1s_2-\vec v_1\cdot\vec v_2,s_1\vec v_2+s_2\vec v_1+\vec v_1\times\vec v_2]
Q1?°Q2?=[s1?,v1?]°[s2?,v2?]=[s1?s2??v1??v2?,s1?v2?+s2?v1?+v1?×v2?]
测试
首先找几个数测试是否等价。
quaternions.py的代码见 自用的四元数、欧拉角、旋转矩阵转换代码。
下面的代码中,为了测试准确,四元数还要保证归一化,不如事先拿几个欧拉角转成四元数。
import numpy as np
from pythonsrc.quaternions import *
e1 = np.array([2, 0.2, -0.1])
e2 = np.array([0.1, 0.2, -0.3])
q1 = Euler_To_Quaternion(e1)
q2 = Euler_To_Quaternion(e2)
q3 = Quaternion_Product(q2, q1)
r1 = Quaternion_to_Rotation(q1)
r2 = Quaternion_to_Rotation(q2)
r3 = Quaternion_to_Rotation(q3)
r4 = r1 @ r2
print(sum(sum(r3-r4)))
然后测试一下 sympy 计算四元数转旋转矩阵的公式是否正确。
import sympy
def Antisymmetric(mat):
ans = sympy.Matrix([
[0, -mat[2], mat[1]],
[mat[2], 0, -mat[0]],
[-mat[1], mat[0], 0],
])
return ans
qsa, qvxa, qvya, qvza = sympy.symbols('s_a, v_{ax}, v_{ay}, v_{az}')
qsb, qvxb, qvyb, qvzb = sympy.symbols('s_b, v_{bx}, v_{by}, v_{bz}')
qva = sympy.Matrix([qvxa, qvya, qvza])
qvb = sympy.Matrix([qvxb, qvyb, qvzb])
result = (qsa**2 - qva.T.dot(qva))*sympy.eye(3)
result += 2*qva*qva.T
result += 2*qsa*Antisymmetric(qva)
sympy.print_latex(result)
输出结果如下
[
s
a
2
+
v
a
x
2
?
v
a
y
2
?
v
a
z
2
?
2
s
a
v
a
z
+
2
v
a
x
v
a
y
2
s
a
v
a
y
+
2
v
a
x
v
a
z
2
s
a
v
a
z
+
2
v
a
x
v
a
y
s
a
2
?
v
a
x
2
+
v
a
y
2
?
v
a
z
2
?
2
s
a
v
a
x
+
2
v
a
y
v
a
z
?
2
s
a
v
a
y
+
2
v
a
x
v
a
z
2
s
a
v
a
x
+
2
v
a
y
v
a
z
s
a
2
?
v
a
x
2
?
v
a
y
2
+
v
a
z
2
]
\left[\begin{matrix}s_{a}^{2} + v_{ax}^{2} - v_{ay}^{2} - v_{az}^{2} & - 2 s_{a} v_{az} + 2 v_{ax} v_{ay} & 2 s_{a} v_{ay} + 2 v_{ax} v_{az}\\2 s_{a} v_{az} + 2 v_{ax} v_{ay} & s_{a}^{2} - v_{ax}^{2} + v_{ay}^{2} - v_{az}^{2} & - 2 s_{a} v_{ax} + 2 v_{ay} v_{az}\\- 2 s_{a} v_{ay} + 2 v_{ax} v_{az} & 2 s_{a} v_{ax} + 2 v_{ay} v_{az} & s_{a}^{2} - v_{ax}^{2} - v_{ay}^{2} + v_{az}^{2}\end{matrix}\right]
?sa2?+vax2??vay2??vaz2?2sa?vaz?+2vax?vay??2sa?vay?+2vax?vaz???2sa?vaz?+2vax?vay?sa2??vax2?+vay2??vaz2?2sa?vax?+2vay?vaz??2sa?vay?+2vax?vaz??2sa?vax?+2vay?vaz?sa2??vax2??vay2?+vaz2??
?
正式验证
最后正式验证等价性。
import sympy
def Antisymmetric(mat):
ans = sympy.Matrix([
[0, -mat[2], mat[1]],
[mat[2], 0, -mat[0]],
[-mat[1], mat[0], 0],
])
return ans
def Quaternion_to_Rotation(Q):
q0, q1, q2, q3 = Q
return sympy.Matrix([
[q0*q0+q1*q1-q2*q2-q3*q3, 2*q1*q2-2*q0*q3, 2*q1*q3+2*q0*q2],
[2*q1*q2+2*q0*q3, q0*q0-q1*q1+q2*q2-q3*q3, 2*q2*q3-2*q0*q1],
[2*q1*q3-2*q0*q2, 2*q2*q3+2*q0*q1, q0*q0-q1*q1-q2*q2+q3*q3],
])
def Quaternion_Product(Q1, Q2):
w1, x1, y1, z1 = Q1
w2, x2, y2, z2 = Q2
w = w1 * w2 - x1 * x2 - y1 * y2 - z1 * z2
x = w1 * x2 + x1 * w2 + y1 * z2 - z1 * y2
y = w1 * y2 + y1 * w2 + z1 * x2 - x1 * z2
z = w1 * z2 + z1 * w2 + x1 * y2 - y1 * x2
return sympy.Matrix([w, x, y, z])
qsa, qvxa, qvya, qvza = sympy.symbols('s_a, v_{ax}, v_{ay}, v_{az}')
qsb, qvxb, qvyb, qvzb = sympy.symbols('s_b, v_{bx}, v_{by}, v_{bz}')
Qa = sympy.Matrix([qsa, qvxa, qvya, qvza])
Qb = sympy.Matrix([qsb, qvxb, qvyb, qvzb])
Qc = Quaternion_Product(Qa, Qb)
Ra = Quaternion_to_Rotation(Qa)
Rb = Quaternion_to_Rotation(Qb)
Rc = Quaternion_to_Rotation(Qc)
Rd = Ra @ Rb
sympy.print_latex(Rc)
sympy.print_latex(Rd)
err = Rc - Rd
sympy.print_latex(err.expand())
输出结果如下,公式特别复杂,两个矩阵的误差为0。
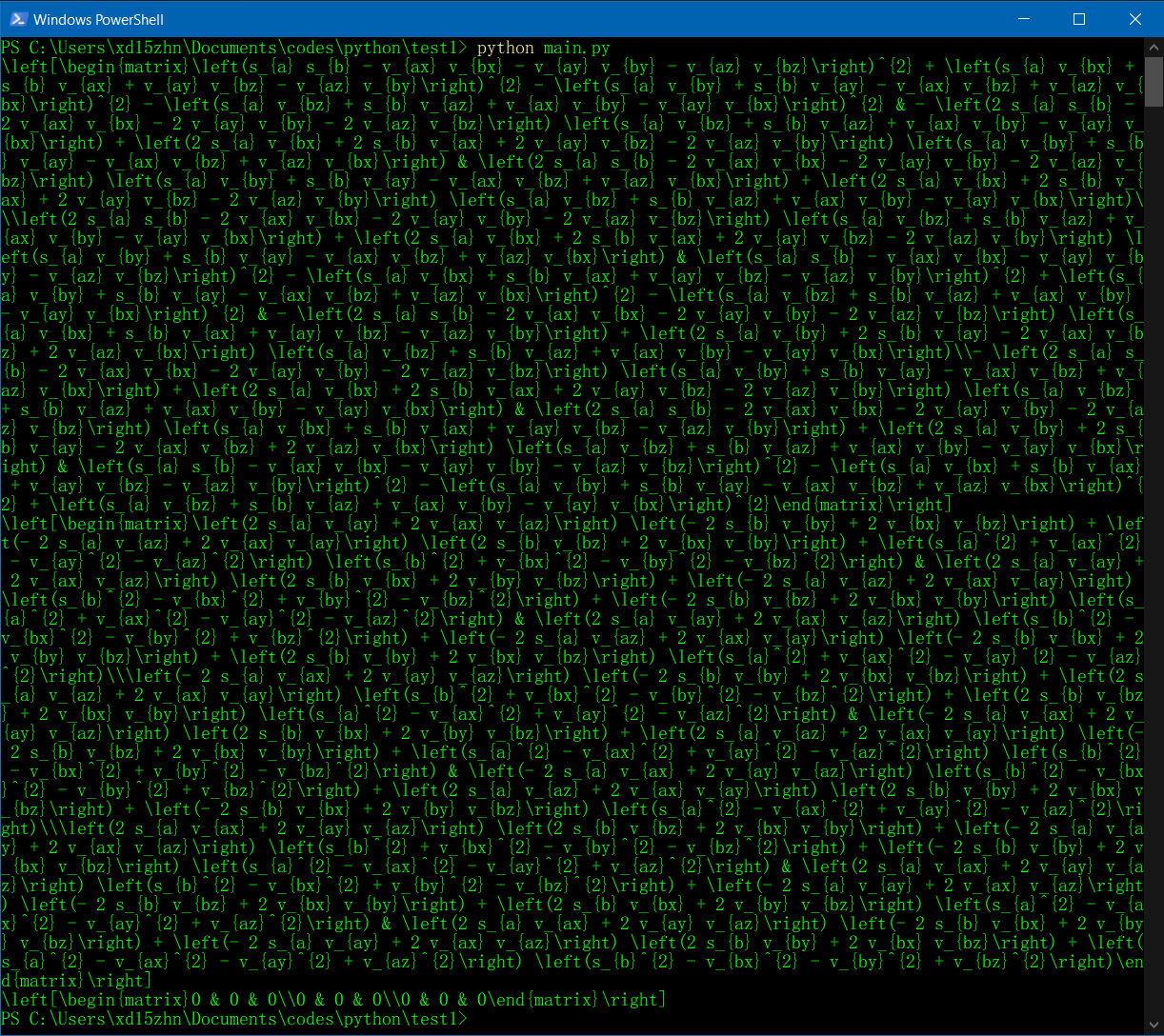
[
(
s
a
s
b
?
v
a
x
v
b
x
?
v
a
y
v
b
y
?
v
a
z
v
b
z
)
2
+
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
?
v
a
z
v
b
y
)
2
?
(
s
a
v
b
y
+
s
b
v
a
y
?
v
a
x
v
b
z
+
v
a
z
v
b
x
)
2
?
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
?
v
a
y
v
b
x
)
2
?
(
2
s
a
s
b
?
2
v
a
x
v
b
x
?
2
v
a
y
v
b
y
?
2
v
a
z
v
b
z
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
?
v
a
y
v
b
x
)
+
(
2
s
a
v
b
x
+
2
s
b
v
a
x
+
2
v
a
y
v
b
z
?
2
v
a
z
v
b
y
)
(
s
a
v
b
y
+
s
b
v
a
y
?
v
a
x
v
b
z
+
v
a
z
v
b
x
)
(
2
s
a
s
b
?
2
v
a
x
v
b
x
?
2
v
a
y
v
b
y
?
2
v
a
z
v
b
z
)
(
s
a
v
b
y
+
s
b
v
a
y
?
v
a
x
v
b
z
+
v
a
z
v
b
x
)
+
(
2
s
a
v
b
x
+
2
s
b
v
a
x
+
2
v
a
y
v
b
z
?
2
v
a
z
v
b
y
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
?
v
a
y
v
b
x
)
(
2
s
a
s
b
?
2
v
a
x
v
b
x
?
2
v
a
y
v
b
y
?
2
v
a
z
v
b
z
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
?
v
a
y
v
b
x
)
+
(
2
s
a
v
b
x
+
2
s
b
v
a
x
+
2
v
a
y
v
b
z
?
2
v
a
z
v
b
y
)
(
s
a
v
b
y
+
s
b
v
a
y
?
v
a
x
v
b
z
+
v
a
z
v
b
x
)
(
s
a
s
b
?
v
a
x
v
b
x
?
v
a
y
v
b
y
?
v
a
z
v
b
z
)
2
?
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
?
v
a
z
v
b
y
)
2
+
(
s
a
v
b
y
+
s
b
v
a
y
?
v
a
x
v
b
z
+
v
a
z
v
b
x
)
2
?
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
?
v
a
y
v
b
x
)
2
?
(
2
s
a
s
b
?
2
v
a
x
v
b
x
?
2
v
a
y
v
b
y
?
2
v
a
z
v
b
z
)
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
?
v
a
z
v
b
y
)
+
(
2
s
a
v
b
y
+
2
s
b
v
a
y
?
2
v
a
x
v
b
z
+
2
v
a
z
v
b
x
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
?
v
a
y
v
b
x
)
?
(
2
s
a
s
b
?
2
v
a
x
v
b
x
?
2
v
a
y
v
b
y
?
2
v
a
z
v
b
z
)
(
s
a
v
b
y
+
s
b
v
a
y
?
v
a
x
v
b
z
+
v
a
z
v
b
x
)
+
(
2
s
a
v
b
x
+
2
s
b
v
a
x
+
2
v
a
y
v
b
z
?
2
v
a
z
v
b
y
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
?
v
a
y
v
b
x
)
(
2
s
a
s
b
?
2
v
a
x
v
b
x
?
2
v
a
y
v
b
y
?
2
v
a
z
v
b
z
)
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
?
v
a
z
v
b
y
)
+
(
2
s
a
v
b
y
+
2
s
b
v
a
y
?
2
v
a
x
v
b
z
+
2
v
a
z
v
b
x
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
?
v
a
y
v
b
x
)
(
s
a
s
b
?
v
a
x
v
b
x
?
v
a
y
v
b
y
?
v
a
z
v
b
z
)
2
?
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
?
v
a
z
v
b
y
)
2
?
(
s
a
v
b
y
+
s
b
v
a
y
?
v
a
x
v
b
z
+
v
a
z
v
b
x
)
2
+
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
?
v
a
y
v
b
x
)
2
]
\left[\begin{matrix}\left(s_{a} s_{b} - v_{ax} v_{bx} - v_{ay} v_{by} - v_{az} v_{bz}\right)^{2} + \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right)^{2} - \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right)^{2} - \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)^{2} & - \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right) + \left(2 s_{a} v_{bx} + 2 s_{b} v_{ax} + 2 v_{ay} v_{bz} - 2 v_{az} v_{by}\right) \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right) & \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right) + \left(2 s_{a} v_{bx} + 2 s_{b} v_{ax} + 2 v_{ay} v_{bz} - 2 v_{az} v_{by}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)\\\left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right) + \left(2 s_{a} v_{bx} + 2 s_{b} v_{ax} + 2 v_{ay} v_{bz} - 2 v_{az} v_{by}\right) \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right) & \left(s_{a} s_{b} - v_{ax} v_{bx} - v_{ay} v_{by} - v_{az} v_{bz}\right)^{2} - \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right)^{2} + \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right)^{2} - \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)^{2} & - \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right) + \left(2 s_{a} v_{by} + 2 s_{b} v_{ay} - 2 v_{ax} v_{bz} + 2 v_{az} v_{bx}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)\\- \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right) + \left(2 s_{a} v_{bx} + 2 s_{b} v_{ax} + 2 v_{ay} v_{bz} - 2 v_{az} v_{by}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right) & \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right) + \left(2 s_{a} v_{by} + 2 s_{b} v_{ay} - 2 v_{ax} v_{bz} + 2 v_{az} v_{bx}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right) & \left(s_{a} s_{b} - v_{ax} v_{bx} - v_{ay} v_{by} - v_{az} v_{bz}\right)^{2} - \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right)^{2} - \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right)^{2} + \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)^{2}\end{matrix}\right]
?(sa?sb??vax?vbx??vay?vby??vaz?vbz?)2+(sa?vbx?+sb?vax?+vay?vbz??vaz?vby?)2?(sa?vby?+sb?vay??vax?vbz?+vaz?vbx?)2?(sa?vbz?+sb?vaz?+vax?vby??vay?vbx?)2(2sa?sb??2vax?vbx??2vay?vby??2vaz?vbz?)(sa?vbz?+sb?vaz?+vax?vby??vay?vbx?)+(2sa?vbx?+2sb?vax?+2vay?vbz??2vaz?vby?)(sa?vby?+sb?vay??vax?vbz?+vaz?vbx?)?(2sa?sb??2vax?vbx??2vay?vby??2vaz?vbz?)(sa?vby?+sb?vay??vax?vbz?+vaz?vbx?)+(2sa?vbx?+2sb?vax?+2vay?vbz??2vaz?vby?)(sa?vbz?+sb?vaz?+vax?vby??vay?vbx?)??(2sa?sb??2vax?vbx??2vay?vby??2vaz?vbz?)(sa?vbz?+sb?vaz?+vax?vby??vay?vbx?)+(2sa?vbx?+2sb?vax?+2vay?vbz??2vaz?vby?)(sa?vby?+sb?vay??vax?vbz?+vaz?vbx?)(sa?sb??vax?vbx??vay?vby??vaz?vbz?)2?(sa?vbx?+sb?vax?+vay?vbz??vaz?vby?)2+(sa?vby?+sb?vay??vax?vbz?+vaz?vbx?)2?(sa?vbz?+sb?vaz?+vax?vby??vay?vbx?)2(2sa?sb??2vax?vbx??2vay?vby??2vaz?vbz?)(sa?vbx?+sb?vax?+vay?vbz??vaz?vby?)+(2sa?vby?+2sb?vay??2vax?vbz?+2vaz?vbx?)(sa?vbz?+sb?vaz?+vax?vby??vay?vbx?)?(2sa?sb??2vax?vbx??2vay?vby??2vaz?vbz?)(sa?vby?+sb?vay??vax?vbz?+vaz?vbx?)+(2sa?vbx?+2sb?vax?+2vay?vbz??2vaz?vby?)(sa?vbz?+sb?vaz?+vax?vby??vay?vbx?)?(2sa?sb??2vax?vbx??2vay?vby??2vaz?vbz?)(sa?vbx?+sb?vax?+vay?vbz??vaz?vby?)+(2sa?vby?+2sb?vay??2vax?vbz?+2vaz?vbx?)(sa?vbz?+sb?vaz?+vax?vby??vay?vbx?)(sa?sb??vax?vbx??vay?vby??vaz?vbz?)2?(sa?vbx?+sb?vax?+vay?vbz??vaz?vby?)2?(sa?vby?+sb?vay??vax?vbz?+vaz?vbx?)2+(sa?vbz?+sb?vaz?+vax?vby??vay?vbx?)2?
?
[
(
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
?
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
+
(
?
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
+
(
s
a
2
+
v
a
x
2
?
v
a
y
2
?
v
a
z
2
)
(
s
b
2
+
v
b
x
2
?
v
b
y
2
?
v
b
z
2
)
(
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
+
(
?
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
s
b
2
?
v
b
x
2
+
v
b
y
2
?
v
b
z
2
)
+
(
?
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
(
s
a
2
+
v
a
x
2
?
v
a
y
2
?
v
a
z
2
)
(
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
s
b
2
?
v
b
x
2
?
v
b
y
2
+
v
b
z
2
)
+
(
?
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
?
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
+
(
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
(
s
a
2
+
v
a
x
2
?
v
a
y
2
?
v
a
z
2
)
(
?
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
?
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
+
(
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
s
b
2
+
v
b
x
2
?
v
b
y
2
?
v
b
z
2
)
+
(
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
(
s
a
2
?
v
a
x
2
+
v
a
y
2
?
v
a
z
2
)
(
?
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
+
(
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
?
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
+
(
s
a
2
?
v
a
x
2
+
v
a
y
2
?
v
a
z
2
)
(
s
b
2
?
v
b
x
2
+
v
b
y
2
?
v
b
z
2
)
(
?
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
s
b
2
?
v
b
x
2
?
v
b
y
2
+
v
b
z
2
)
+
(
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
+
(
?
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
(
s
a
2
?
v
a
x
2
+
v
a
y
2
?
v
a
z
2
)
(
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
+
(
?
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
s
b
2
+
v
b
x
2
?
v
b
y
2
?
v
b
z
2
)
+
(
?
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
(
s
a
2
?
v
a
x
2
?
v
a
y
2
+
v
a
z
2
)
(
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
s
b
2
?
v
b
x
2
+
v
b
y
2
?
v
b
z
2
)
+
(
?
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
?
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
+
(
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
(
s
a
2
?
v
a
x
2
?
v
a
y
2
+
v
a
z
2
)
(
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
?
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
+
(
?
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
+
(
s
a
2
?
v
a
x
2
?
v
a
y
2
+
v
a
z
2
)
(
s
b
2
?
v
b
x
2
?
v
b
y
2
+
v
b
z
2
)
]
\left[\begin{matrix}\left(2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(- 2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) + \left(- 2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) + \left(s_{a}^{2} + v_{ax}^{2} - v_{ay}^{2} - v_{az}^{2}\right) \left(s_{b}^{2} + v_{bx}^{2} - v_{by}^{2} - v_{bz}^{2}\right) & \left(2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) + \left(- 2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(s_{b}^{2} - v_{bx}^{2} + v_{by}^{2} - v_{bz}^{2}\right) + \left(- 2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) \left(s_{a}^{2} + v_{ax}^{2} - v_{ay}^{2} - v_{az}^{2}\right) & \left(2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(s_{b}^{2} - v_{bx}^{2} - v_{by}^{2} + v_{bz}^{2}\right) + \left(- 2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(- 2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) + \left(2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) \left(s_{a}^{2} + v_{ax}^{2} - v_{ay}^{2} - v_{az}^{2}\right)\\\left(- 2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(- 2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) + \left(2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(s_{b}^{2} + v_{bx}^{2} - v_{by}^{2} - v_{bz}^{2}\right) + \left(2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) \left(s_{a}^{2} - v_{ax}^{2} + v_{ay}^{2} - v_{az}^{2}\right) & \left(- 2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) + \left(2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(- 2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) + \left(s_{a}^{2} - v_{ax}^{2} + v_{ay}^{2} - v_{az}^{2}\right) \left(s_{b}^{2} - v_{bx}^{2} + v_{by}^{2} - v_{bz}^{2}\right) & \left(- 2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(s_{b}^{2} - v_{bx}^{2} - v_{by}^{2} + v_{bz}^{2}\right) + \left(2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) + \left(- 2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) \left(s_{a}^{2} - v_{ax}^{2} + v_{ay}^{2} - v_{az}^{2}\right)\\\left(2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) + \left(- 2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(s_{b}^{2} + v_{bx}^{2} - v_{by}^{2} - v_{bz}^{2}\right) + \left(- 2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) \left(s_{a}^{2} - v_{ax}^{2} - v_{ay}^{2} + v_{az}^{2}\right) & \left(2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(s_{b}^{2} - v_{bx}^{2} + v_{by}^{2} - v_{bz}^{2}\right) + \left(- 2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(- 2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) + \left(2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) \left(s_{a}^{2} - v_{ax}^{2} - v_{ay}^{2} + v_{az}^{2}\right) & \left(2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(- 2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) + \left(- 2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) + \left(s_{a}^{2} - v_{ax}^{2} - v_{ay}^{2} + v_{az}^{2}\right) \left(s_{b}^{2} - v_{bx}^{2} - v_{by}^{2} + v_{bz}^{2}\right)\end{matrix}\right]
?(2sa?vay?+2vax?vaz?)(?2sb?vby?+2vbx?vbz?)+(?2sa?vaz?+2vax?vay?)(2sb?vbz?+2vbx?vby?)+(sa2?+vax2??vay2??vaz2?)(sb2?+vbx2??vby2??vbz2?)(?2sa?vax?+2vay?vaz?)(?2sb?vby?+2vbx?vbz?)+(2sa?vaz?+2vax?vay?)(sb2?+vbx2??vby2??vbz2?)+(2sb?vbz?+2vbx?vby?)(sa2??vax2?+vay2??vaz2?)(2sa?vax?+2vay?vaz?)(2sb?vbz?+2vbx?vby?)+(?2sa?vay?+2vax?vaz?)(sb2?+vbx2??vby2??vbz2?)+(?2sb?vby?+2vbx?vbz?)(sa2??vax2??vay2?+vaz2?)?(2sa?vay?+2vax?vaz?)(2sb?vbx?+2vby?vbz?)+(?2sa?vaz?+2vax?vay?)(sb2??vbx2?+vby2??vbz2?)+(?2sb?vbz?+2vbx?vby?)(sa2?+vax2??vay2??vaz2?)(?2sa?vax?+2vay?vaz?)(2sb?vbx?+2vby?vbz?)+(2sa?vaz?+2vax?vay?)(?2sb?vbz?+2vbx?vby?)+(sa2??vax2?+vay2??vaz2?)(sb2??vbx2?+vby2??vbz2?)(2sa?vax?+2vay?vaz?)(sb2??vbx2?+vby2??vbz2?)+(?2sa?vay?+2vax?vaz?)(?2sb?vbz?+2vbx?vby?)+(2sb?vbx?+2vby?vbz?)(sa2??vax2??vay2?+vaz2?)?(2sa?vay?+2vax?vaz?)(sb2??vbx2??vby2?+vbz2?)+(?2sa?vaz?+2vax?vay?)(?2sb?vbx?+2vby?vbz?)+(2sb?vby?+2vbx?vbz?)(sa2?+vax2??vay2??vaz2?)(?2sa?vax?+2vay?vaz?)(sb2??vbx2??vby2?+vbz2?)+(2sa?vaz?+2vax?vay?)(2sb?vby?+2vbx?vbz?)+(?2sb?vbx?+2vby?vbz?)(sa2??vax2?+vay2??vaz2?)(2sa?vax?+2vay?vaz?)(?2sb?vbx?+2vby?vbz?)+(?2sa?vay?+2vax?vaz?)(2sb?vby?+2vbx?vbz?)+(sa2??vax2??vay2?+vaz2?)(sb2??vbx2??vby2?+vbz2?)?
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!