＜蓝桥杯软件赛＞零基础备赛20周--第10周--二分

报名明年4月蓝桥杯软件赛的同学们，如果你是大一零基础，目前懵懂中，不知该怎么办，可以看看本博客系列：备赛20周合集
20周的完整安排请点击：20周计划
每周发1个博客，共20周（读者可以按自己的进度选“正常”和“快进”两种计划）。
每周3次集中答疑，周三、周五、周日晚上，在QQ群上答疑：

第9周: ?二分

备赛20周活动已经到第10周了，也快到期末考试阶段了。大家先准备考试，有空做做竞赛题。

1. 二分基础

??二分是蓝桥杯省赛的必考知识点，每年都有。本文的例题大多都是蓝桥杯省赛真题。
??（本博主曾写过一篇 二分法、三分法，非常详细地介绍了二分法的原理和例题，请参考。今天这篇博客，介绍了二分的基础内容，以及在蓝桥杯中的应用。）

1.1 二分概念

??“二分法”是一种思路简单、编码容易、效率极高、应用广泛的算法。在任何算法竞赛中，二分法都是最常见的知识点之一。
??二分法的思想很简单，每次把搜索范围缩小一倍，直到找到答案为止。
??设初始范围是[L, R]，常见的二分法代码这样写：

while (L < R){                      //一直二分，直到区间[L,R]缩小到L=R
    int mid = (L + R) / 2;          //mid是L、R的中间值
    if (check(mid))  R = mid;       //答案在左半部分[L,mid]，更新R=mid
    else             L = mid + 1;   //答案在右半部分[mid+1, R]，更新L=mid+1
}

??答案在区间[L, R]中，通过中间值mid缩小搜索范围。这样搜索答案：
??（1）如果答案在左半部分，把范围缩小到[L, mid]，更新R=mid，然后继续。
??（2）如果答案在右半部分，把范围缩小到[mid+1, R]，更新L=mid+1，然后继续。
??经过多次二分，最后范围缩小到L=R，这就是答案。
??二分的效率极高，例如在$10亿=2^{30}$个数字中查找某个数，前提是这些数已经排序，然后用二分法来找，最多只需找30次。把二分法的计算复杂度记为O(logn)。
??以猜数字游戏为例，一个[1, 100]内的数字，猜7次就能猜出来。例如猜数字68：

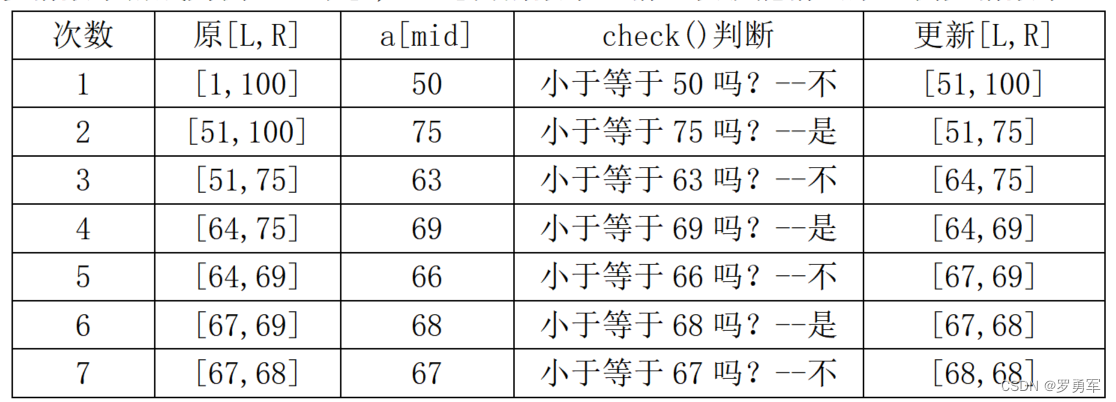
1.2 基本代码

??下面是“猜数游戏”的C++代码实现。二分函数bin_search()操作3个变量：区间左端点L、右端点R、二分的中位数mid。每次把区间缩小一半，把L或R更新为mid；直到L= R为止，即找到了答案所处的位置。

#include<bits/stdc++.h>
using namespace std;
int a[105];
bool check(int x,int mid){            //二分中的检查函数
    return x <= a[mid];               //如果x小于等于中间数，返回true
}
int bin_search(int n, int x){         //在数组a中找数字x，返回位置
    int L = 1, R = n;                 //初始范围[L, R]
    while (L < R) {
        int mid = (L+R)/2;
        if (check(x,mid)) R = mid;    //答案在左半部分:[L,mid]
        else              L = mid+1;  //答案在右半部分:[mid+1, R]
    }
   return a[L];                       //返回答案
}
int main(){
    int n = 100;
    for(int i=1;i<=n;i++) a[i]=i;      //赋值，数字1~100
    int x = 68;                        //猜68这个数
    cout<<"x="<<bin_search(n,x);
}

Java代码

import java.util.*;
class Main {
    static int[] a = new int[105];
    static boolean check(int x, int mid) { return x <= a[mid]; }
    static int bin_search(int n, int x) {
        int L = 1;
        int R = n;
        while (L < R) {
            int mid = (L + R) / 2;
            if (check(x, mid))     R = mid;
            else                   L = mid + 1;            
        }
        return a[L];
    }

    public static void main(String[] args) {
        int n = 100;
        for (int i = 1; i <= n; i++)   a[i] = i;        
        int x = 68;
        System.out.println("x=" + bin_search(n, x));
    }
}

Python代码

def check(x, mid): return x <= a[mid]
def bin_search(n, x):
    L, R = 1, n
    while L < R:
        mid = (L+R) // 2
        if check(x, mid):     R = mid
        else:                 L = mid + 1
    return a[L]

n = 100
a = [0] * 105
for i in range(1, n + 1):   a[i] = i
x = 68
print("x=", bin_search(n, x))

1.3 二分的应用条件

??二分法把长度为n的有序序列上O(n)的查找时间，优化到了O(logn)。

??注意二分法的应用条件是：序列是单调有序的，从小到大，或从大到小。在无序的序列上无法二分，如果是乱序的，应该先排序再二分。
??如果在乱序序列上只搜一次，不需要用二分法。如果用二分，需要先排序，排序复杂度O(nlogn)，再二分是O(logn)，排序加二分的总复杂度O(nlogn)。如果用暴力法直接在乱序的n个数里面找，复杂度是O(n)的，比排序加二分快。
??但是如果不是搜一个数，而是搜m个数。那么先排序再做m次二分的计算复杂度是O(nlogn+mlogn)，而暴力法是O(mn)的，当m很大时，二分法远好于暴力法。
??做二分法题目时，需要建模出一个有序的序列，并且答案在这个序列中。编程时，根据题目要求确定区间[L, R]范围，并写一个check()函数来更新L和R。

1.4 中值mid的计算方法

??[L, R]的中间值mid，有多种计算方法：
????mid = (L+R)/2
????mid = (L+R)>>1
????mid = L+(R-L)/2
??下表（《算法竞赛》清华大学出版社45页）对比了它们的优缺点。一般情况下，用哪个都行。

2. 经典应用：最小值最大化、最大值最小化

??二分法的经典应用场景是“最小值最大化（最小值尽量大）”、“最大值最小化（最大值尽量小）”。
（1）最小值最大化
??有n个牛棚，分布在一条直线上，有k头牛，给每头牛安排一个牛棚住，k<n。由于牛脾气很大，所以希望让牛之间尽量住得远一些。这个问题简化为：在一条直线上有n个点，选k个点，其中某两点之间的距离是所有距离中最小的，求解目标是让这个最小距离尽量大。这就是“最小值（两点间的最小距离）最大化”。
??“牛棚问题”的求解可以用猜的方法。猜最小距离是D，看能不能在n个点中选k个，使得任意两点之间的距离≥D。如果可以，说明D是一个合法的距离。然后猜新的D，直到找到那个最大的合法的D。
??具体操作是：从第1个点出发，然后逐个检查后面的点，第一个距离≥D的点，就是选中的第2点；然后从第2点出发，再选后面第一个距离第2点≥D的点，这是选中的第3点；…继续下去，直到检查完n个点。这一轮猜测的计算复杂度是O(n)的。
??检查完n个点，如果选中的点的数量≥k，说明D猜小了，下次猜大点；如果选中的点的数量<k，说明D猜大了，下次猜小点。
??如何猜D？简单的办法是从小到大一个个试，但是计算量太大了。
??用二分法可以加速猜D的过程。设D的初值是一个极大的数，例如就是所有n点的总长度L。接下来的二分操作和前面的“猜数字游戏”一样，经过O(logL)次，就能确定D。
??总计算量：一共O(logL)轮猜测，每一轮O(n)，总计算量为O(nlogL)。
（2）最大值最小化
??经典的例子是“序列划分”问题。有一个包含n个正整数的序列，把它划分成k个子序列，每个子序列是原数列的一个连续部分，第i个子序列的和为Si。在所有s中，有一个最大值。问如何划分，才能使最大的s最小？这就是“最大值（所有子序列和的最大值）最小化”。
??例如序列{2, 2, 3, 4, 5, 1}，将其划分成k=3个连续的子序列。下面举例2种分法：{(2, 2, 3)、(4, 5)、(1)}，子序列和分别是7、9、1，最大值是9；{(2, 2, 3)、(4)、(5,1)}，子序列和是7、4、6，最大值是7。第2种分法比第1种好。
??仍然用猜的方法。在一次划分中猜一个x，对任意的Si都有Si ≤ x，也就是说，x是所有Si中的最大值。
??如何找到这个x？简单的办法是枚举每一个x，用贪心法每次从左向右尽量多划分元素，Si不能超过x，划分的子序列个数为k个。但是枚举所有的x太耗时了。
??用二分法可以加速猜x的过程。用二分法在[max, sum]范围内查找满足条件的x，其中max是序列中最大元素的值，sum是所有元素的和。

3. 例题

3.1 简单二分：求阶乘

蓝桥杯2022初赛题：求阶乘
链接1
链接2
题解：
??尾零是2×5相乘得到的，所以只需要计算n!中2和5的因子的数量。又因为n!中2的因子数量远大于5的因子数量，所以只需要计算5的因子数量。
??例如25!=25×…×20×…×15×…×10×…×5×…，其中的25、20、15、10、5分别有2、1、1、1、1共6个因子5，所以尾零有6个。
（1）通过30%测试。
??简单的方法是检查每个n，计算n!的尾零数量，尾零数量等于k的n就是答案。下面代码第11行的for循环n/5次，对于100%的数据，$1\le K\le 10^{18}$，由于n比k还大，代码超时。
??函数check(n)返回n!的尾零数量，也就是计算n!有多少个因子5，读者可以按自己的思路实现这个函数。下面的check()用了巧妙的方法。以25!为例，对5有贡献的是5、10、15、20、25，即5×1、5×2、5×3、5×4、5×5，共有6个5，其中5个5是25/5得到的，即5×i中的5；还有一个5是循环5次后多了一个5，即i×5的5。再例如100!，尾零的数量包括两部分：100/5=20、20/5=4。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll check(ll n) {                //计算n!末尾有多少个0
    ll cnt = 0;
    while (n)  cnt += (n /= 5);  
    return cnt;
}
int main(){
    ll k;  cin >> k;
    for(ll n=5;;n+=5){          //n是5的倍数，它含有因子5
        ll cnt = check(n);      //cnt是n!的尾零数量
        if(cnt==k){ cout << n; break;}
        if(cnt>k) { cout <<-1; break;}
    }
    return 0;
}

（2）通过100%测试。
??本题容易想到可以用二分优化，也就是用二分来猜n。因为n递增时，尾零的数量也是单调递增的，符合二分法的应用条件。
??下面讨论代码的计算复杂度。第12行的二分是$O(logE)$，这里$E=10^{19}$。第4行做一次check()差不多是O(1)的。总计算量约为$logE=log10^{19}$ < 70次。
C++代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll check(ll n) {              //计算n!末尾有多少个0
    ll cnt = 0;
    while (n)  cnt += (n /= 5);
    return cnt;
}
int main() {
    ll k;  cin >> k;
    ll L = 0, R = 1e19;       //R的初值为一个极大的数
    while (L < R) {
        ll mid = (L + R) >> 1;
        if (check(mid) >= k)   R = mid;     // mid!的尾零数量超过了k，说明mid大了
        else                   L = mid + 1; // mid小了
    }
    if (check(R) == k)  cout << R ;
    else                cout << -1;
    return 0;
}

java代码

import java.util.Scanner;
public class Main {
    public static long check(long n) {
        long cnt = 0;
        while (n > 0) {
            cnt += n / 5;
            n /= 5;
        }
        return cnt;
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        long k = scanner.nextLong();
        long L = 0;
        long R = (long) Math.pow(10, 19);
        while (L < R) {
            long mid = (L + R) / 2;
            if (check(mid) >= k)   R = mid;
            else                   L = mid + 1;
        }
        if (check(R) == k)    System.out.println(R);
        else                  System.out.println(-1);
    }
}

python代码

def check(n):
    cnt = 0
    while n:
        cnt += n // 5
        n //= 5
    return cnt
k = int(input())
L = 0
R = 10**19
while L < R:
    mid = (L + R) // 2
    if check(mid) >= k:    R = mid
    else:        L = mid + 1
if check(R) == k:   print(R)
else:               print(-1)

3.2 简单二分：分巧克力

分巧克力： 2017年第八届蓝桥杯省赛
链接1
链接2
题解：
（1）通过50%的测试。
??先试试暴力法：把边长从1开始到最大边长d，每个值都试一遍，一直试到刚好够分的最大边长为止。编码：边长初始值d = 1，然后d = 2, 3, 4, …一个个试。

#include<bits/stdc++.h>
using namespace std;
int h[100010],w[100010];
int n,k;
bool check(int d){              //检查够不够分
    int num=0;
    for(int i=0;i<n;i++)  num += (h[i]/d)*(w[i]/d);
    if(num>=k) return true;     //够分
    else       return false;    //不够分
}
int main(){
    cin >>n>>k;
    for(int i=0;i<n;i++)  cin>>h[i]>>w[i];
    int d=1;                    //正方形边长
    while(1){
        if(check(d))  d++;      //边长从1开始，一个个地暴力试
        else          break;
    }
    cout << d-1;
    return 0;
}

??暴力法的复杂度：n个长方形，长方形的最大边长d。第16行check()一次的计算量是O(n)，需要做d次check()，总复杂度O(n×d)，而n和d的最大值是$10^5$，超时。
(2)通过100%测试
??一个个试边长d太慢了，现在使用二分，按前面的“猜数游戏”的方法猜d的取值。暴力法需要做d次check()，现在用二分法，只需要做O(logd)次check()。具体操作是：
??第一次：开始时d的范围是1~D，试试中间值D/2，如果这个值大了，就把范围缩小为0 ~ D/2，如果这个值小了，就把范围缩小为D/2 ~ D；
??第二次，取新的中间值D/4或3D/4，再试…
??…
??直到找到合适的值为止。
C++代码
??整数的二分法的编码虽然简单，但是很容易出错。左右边界L、R和中间值mid的迭代，由于整数的取整问题，极易出错，导致死循环。下面的代码给出了两种写法，有细微而关键的区别，请仔细领会并彻底理解这两种写法。

#include<bits/stdc++.h>
using namespace std;
int n,k;
const int N=100010;
int h[N],w[N];
bool check(int d){
    int num=0;
    for(int i=0;i<n;i++)  num += (h[i]/d)*(w[i]/d);
    if(num>=k) return true;      //够分
    else       return false;     //不够分
}
int main(){
    cin >> n >> k;
    for(int i=0;i<n;i++)   cin>>h[i]>>w[i];
    int L=1, R=N;                //D的初值是R=100010
//第一种写法：
    while(L<R) {
        int mid=(L+R+1)>>1;      //除2，向右取整
        if(check(mid))  L=mid;   //新的搜索区间是右半部分，R不变，调整L=mid
        else            R=mid-1; //新的搜索区间是左半部分，L不变，调整R=mid–1
    }
    cout << L;
//第二种写法：
/*  while(L<R) {
        int mid=(L+R)>>1;        //除2，向左取整
        if(check(mid)) L=mid+1;  //新的搜索区间是右半部分，R不变，更新L=mid+1
        else           R=mid;    //新的搜索区间是左半部分，L不变，更新R=mid
    }
    cout << L-1;    */
    return 0;
}

java代码

import java.util.Scanner;

public class Main {
    static int n, k;
    static final int N = 100010;
    static int[] h = new int[N];
    static int[] w = new int[N];

    static boolean check(int d) {
        int num = 0;
        for (int i = 0; i < n; i++)
            num += (h[i] / d) * (w[i] / d);
        if (num >= k)         return true; // 够分
        else            return false; // 不够分
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        k = scanner.nextInt();
        for (int i = 0; i < n; i++) {
            h[i] = scanner.nextInt();
            w[i] = scanner.nextInt();
        }
        int L = 1, R = N; // D的初值是R=100010
        while (L < R) {
            int mid = (L + R + 1) >> 1; // 除2，向右取整
            if (check(mid)) L = mid; // 新的搜索区间是右半部分，R不变，调整L=mid
            else          R = mid - 1; // 新的搜索区间是左半部分，L不变，调整R=mid–1
        }
        System.out.println(L);
        scanner.close();
    }
}

python代码

def check(d):
    global w,h
    num = 0
    for i in range(len(w)):
        num += (w[i]//d) * (h[i]//d)
    if num >= k:  return True
    return False
n,k = map(int,input().split())
w = []
h = []
for i in range(n):
    a,b = map(int,input().split())
    w.append(a)
    h.append(b)
L ,R = 1, 100010
while L < R:
    mid = (L+R)//2
    if check(mid):  L = mid +1
    else :          R = mid
print(L-1)

3.3 最小值最大化：跳石头

跳石头：链接
??这是一道二分法应用的套路题：“最小值最大化”。
??在n块岩石中移走m个石头，有很多种移动方法。在第i种移动方法中，剩下的石头之间的距离，有一个最小距离ai。在所有移动方法的最小距离ai中，问最大的ai是多少。
??在所有可能的最小值中，找最大的那个，就是“最小值最大化”。
??如果用暴力法找所有的组合，在n块岩石中选m个石头有n!/m!(n-m)!种组合，情况太多，显然会超时。
??可以转换思路，不去找搬走石头的各种组合，而是给出一个距离d，检查能不能搬走m块石头而得到最短距离d。把所有的d都试一遍，肯定能找到一个最短的d。用二分法找这个d即可。
C++代码
??下面的代码中，17 ~ 21行用二分法找一个最小距离d。函数check(d)函数检查d这个距离是否合适。
??请保证自己能写出代码，确保能完全写出整数二分而不出错。

#include<cstdio>
int len,n,m;
int stone[50005];
bool check(int d){   //检查距离d是否合适
    int num=0;       //num记录搬走石头的数量
    int pos=0;       //当前站立的石头
    for(int i=1;i<=n;++i)
        if(stone[i]-pos < d)  num++;          //第i块石头可以搬走
        else                  pos = stone[i];   //第i块石头不能搬走
    if(num <= m) return true;  //要移动的石头比m少，满足条件
    else return false;         //要移动的石头比m多，不满足条件
}
int main(){
    scanf("%d%d%d",&len,&n,&m);
    for(int i=1;i<=n;++i) scanf("%d",&stone[i]);
    int L=0,R=len,mid;
    while(L<R){
        mid = L+(R-L)/2;
        if(check(mid)) L = mid+1;  //满足条件，说明mid小了，调大一点
        else           R = mid-1;  //不满足条件，说明mid大了，调小一点
    }
    if(!check(L)) L -= 1;
    printf("%d\n",L);
    return 0;
}

java代码

import java.util.Scanner;

public class Main {
    static int len, n, m;
    static int[] stone;

    static boolean check(int d) {
        int num = 0; // num记录搬走石头的数量
        int pos = 0; // 当前站立的石头
        for (int i = 1; i <= n; ++i)
            if (stone[i] - pos < d)         num++; // 第i块石头可以搬走
            else                pos = stone[i]; // 第i块石头不能搬走
        if (num <= m)       return true; // 要移动的石头比m少，满足条件
        else            return false; // 要移动的石头比m多，不满足条件
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        len = scanner.nextInt();
        n = scanner.nextInt();
        m = scanner.nextInt();
        stone = new int[n + 1];
        for (int i = 1; i <= n; ++i)       stone[i] = scanner.nextInt();
        int L = 0, R = len, mid;
        while (L < R) {
            mid = L + (R - L) / 2;
            if (check(mid))  L = mid + 1; // 满足条件，说明mid小了，调大一点
            else             R = mid - 1; // 不满足条件，说明mid大了，调小一点
        }
        if (!check(L))  L -= 1;
        System.out.println(L);
        scanner.close();
    }
}

python代码

len, n, m = map(int, input().split())
stone = []                      # 石头i和到起起点的距离
def check(d):
    num = 0
    pos = 0      
    for i in range(0,n):        # 0到n-1作为石头下标 
        if (stone[i]-pos < d):  # 第i块可以搬走
            num += 1              
        else:  pos = stone[i]
    if num <= m: return True
    else:        return False
for i in range(n):
    t = int(input())
    stone.append(t)
L, R = 0, len
while (L<R):
    mid = L+(R-L)//2
    if check(mid): L = mid+1
    else:          R = mid-1
if check(L):   print(L)
else:          print(L-1)

3.4 简单题：青蛙过河

青蛙过河：2022年第十三届蓝桥杯省赛
链接1 链接2

题解：往返累计2x次相当于单向走2x次。跳跃能力越大，越能保证可以通过2x次。用二分法找到一个最小的满足条件的跳跃能力。设跳跃能力为mid，每次能跳多远就跳多远，用二分法检查mid是否合法。

C++代码

#include<bits/stdc++.h>
using namespace std;
int h[1000005];
int n,x;
bool check(int mid){
    long long sum=0;
    for(int i=0;i<mid-1;i++)  sum+=h[i];  //mid-1个
    for(int i=0, j=mid-1;j<n;i++,j++) {   //青蛙位置i，目标位置j
        sum += h[j];
        if(sum < 2*x)   return false;
        sum -= h[i];
    }
    return true;
}
int main(){
    cin>>n>>x;
    for(int i=1;i<n;i++)  cin>>h[i];
    int left=0, right=n;
    while(left<right){
        int mid=(left+right)/2;
        if(check(mid))  right = mid;
        else            left = mid+1;
    }
    cout<<right;
    return 0;
}

java代码

import java.io.*;
 
public class Main {
    static StreamTokenizer reader = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    static PrintWriter writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
    static int readInt() throws Exception {
        reader.nextToken();
        return (int)reader.nval;
    }
    static int N = 1000010;
    static int[] sum = new int[N];
    static int n, x;
 
    static boolean check(int len) {
        for(int i = 1; i + len <= n; i ++) {
            if(sum[i + len - 1] - sum[i - 1] < x) 
                return false;
        }
        return true;
    }
 
    public static void main(String[] args) throws Exception {
        n = readInt(); x = readInt();
        x *= 2;
        for(int i = 1; i < n; i ++) {
            int t = readInt();
            sum[i] = sum[i - 1] + t;
        }
        int l = 1, r = n;
        while(l < r) {
            int mid = l + r >> 1;
            if(check(mid)) r = mid;
            else l = mid + 1;
        }
        writer.println(l);
        writer.flush();
    }
}

python代码

def check(mid):
    for i in range(mid, n):
        if sum[i] - sum[i-mid] < 2 * x: return False
    return True 
 
n, x = map(int, input().split())
h = list(map(int, input().split()))
sum = [0, h[0]]
for i in range(1, len(h)):
    sum.append(h[i] + sum[i])
L = 0
R = 100000
while L <= R:
    mid = (L + R) // 2
    if check(mid):   R = mid - 1
    else:            L = mid + 1
print(L)

3.5 中等题：技能升级

技能升级：2022年第十三届省赛
链接1
链接2
??下面详细讲解多种方法，它们分别能通过40%、60%、100%的测试。
（1）暴力法：通过40%测试
??先试试暴力法，直接模拟题意，升级m次，每次升级时选用最高攻击力的技能，然后更新它的攻击力。
??下面用Python写代码。复杂度是多少？第12行升级m次，是O(m)的；第13行选用最大攻击，使用了Python的max()函数，是O(n)的。总复杂度O(mn)，只能通过40%的测试。

import math
n,m = map(int,input().split())
a = []                               # 存ai
b = []                               # 存bi
c = []                               # ai/bi
for i in range(n):
    a_,b_ = map(int,input().split())
    a.append(a_)
    b.append(b_)    
    c.append(math.ceil(a_/b_))       #向上取整
ans = 0
for i in range(m):                   #一共升级m次
    max_num = max(a)                 #每次升级时，使用最大的攻击
    index = a.index(max_num )        #最大攻击对应的序号    
    a[index] -= b[index]             #更新攻击力
    if c[index]>0: ans += max_num    #累加攻击力
    c[index] -= 1
print(ans)

（2）暴力法+优先队列：通过60%测试
??上面的代码可以稍做改进。在n个技能中选用最高攻击力，可以使用优先队列，一次操作的复杂度为O(logn)。m次升级，总复杂度O(mlogn)，能通过60%的测试。
??下面用C++的优先队列priority_queue实现。priority_queue默认是大根堆，用top()读取队列中的最大值。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
typedef pair<int, int> PII;
priority_queue<PII> q;               //默认是大根堆
PII p;
int main() {
    int n, m; cin >> n >> m;
    for (int i = 0; i < n; i++) {
        int a, b;  cin >> a >> b;
        q.push(make_pair(a, b));
    }
    long long ans = 0;
    while (m--) {                    //升级m次
        if (q.empty()) break;
        p = q.top(); q.pop();        //每次升级时，使用最大的攻击。读队列最大值并删除
        ans += p.first;              //累加攻击力
        p.first -= p.second;         //更新攻击力
        if (p.first > 0) q.push(p);  //重新放进队列
    }
    cout << ans;
    return 0;
}

java代码

import java.util.PriorityQueue;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        PriorityQueue<PII> q = new PriorityQueue<>((a, b) -> b.first - a.first);
        for (int i = 0; i < n; i++) {
            int a = scanner.nextInt();
            int b = scanner.nextInt();
            q.add(new PII(a, b));
        }
        long ans = 0;
        while (m > 0 && !q.isEmpty()) {
            PII p = q.poll();
            ans += p.first;
            p.first -= p.second;
            if (p.first > 0) q.add(p);
            m--;
        }
        System.out.println(ans);
    }

    static class PII {
        int first;
        int second;

        PII(int first, int second) {
            this.first = first;
            this.second = second;
        }
    }
}

python代码
??Python的“暴力法+优先队列”实现。优先队列用堆实现，heapq默认是小根堆，第7行把a取负，把最大值变成了最小值。

from heapq import *
n,m = map(int,input().split()) 
q = [] 
ans = 0 
for i in range(n):
    a,b = map(int,input().split())
    heappush(q,(-a,b)) 
for i in range(m):
    p = heappop(q)
    a,b = -p[0],p[1]
    ans += a
    a = max(a - b, 0)
    if a != 0: heappush(q,(-a,b)) 
print(ans)

（3）二分法：通过100%测试
??本题的正解是二分法，能通过100%的测试。
??本题$m\le 2\times 10^9$太大，若逐一升级m次必定会超时。但是不能直接对m进行二分，因为需要知道每个技能升级多少次，而这与m无关。
??思考升级技能的过程，是每次找攻击力最高的技能。对某个技能，最后一次升级的攻击力，肯定比之前升级的攻击力小，也就是前面的升级都更大。可以设最后一次升级提升的攻击力是mid，对每个技能，若它最后一次能升级mid，那么它前面的升级都更大。所有这样最后能达到mid的技能，它们前面的升级都应该使用。用二分法找到这个mid，另外，升级技能减少的攻击力的过程是一个等差数列，用O(1)次计算即可知道每个技能升级了几次。知道了每个技能升级的次数，就可以计算一共提升了多少攻击力，这就是题目的答案
??下面给出Python代码。函数check(mid)找这个mid。第6行，若所有技能升级总次数大于等于m次，说明mid设小了，在19行让L增大，即增加了mid。第7行，若所有技能升级总次数小于m次，说明mid设大了，在20行让R减小，即缩小了mid。
??分析代码的复杂度。17~20行，二分$O(logA)$次，这里A表示$1\le Ai\le 10^6$；每次check()是O(n)，二分的总复杂度是O(nlogA)。23行O(n)。代码的总复杂度是O(nlogA) + O(n)，通过100%的测试。
c++代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[100005],b[100005];
int n, m;

bool check(ll mid) {
    ll cnt = 0;
    for (int i = 0; i < n; i++) {
        if (a[i] < mid) continue;
        cnt += (a[i] - mid) / b[i] + 1;
        if (cnt >= m) return true;
    }
    return false;
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++)   cin >> a[i] >> b[i];
    ll L = 1, R = 1000000;
    while (L <= R) {
        ll mid = (L + R) / 2;
        if (check(mid))    L = mid + 1;
        else       R = mid - 1;
    }
    ll attack = 0;
    ll cnt = m;
    for (int i = 0; i < n; i++) {
        if (a[i] < R) continue;
        ll t = (a[i] - L) / b[i] + 1;
        if (a[i] - b[i] * (t - 1) == R) t -1;
        attack += (a[i] * 2 - (t - 1) * b[i]) * t / 2;
        cnt -= t;
    }
    cout << attack + cnt * R << endl;
    return 0;
}

java代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
 
public class Main {
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 65536);
    static StringTokenizer tokenizer = new StringTokenizer("");
    static int maxn = (int) (1e5 + 5);
    static int[] array = new int[maxn];
    static int[] facts = new int[maxn];
    static int n, m;
 
    // 二分枚举最后一次攻击力最高能加多少，并且要注意最后的计算不能把等于这个值的直接加在答案里
    public static void main(String[] args) {
        n = nextInt(); m = nextInt();
        for (int i = 0; i < n; i++) {
            array[i] = nextInt();
            facts[i] = nextInt();
        }
        long ans = 0L;
        // 二分最后一次技能最多提升了多少攻击力
        int l = 0, r = (int) 1e6;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (check(mid)) l = mid;
            else r = mid - 1;
        }
        int x = l;
        for (int i = 0; i < n; i++) {
            if (array[i] >= x) {
                int cnt = (array[i] - x) / facts[i] + 1;
                int last = array[i] - (cnt - 1) * facts[i];
                if (last == x) {
                    cnt--;
                    last += facts[i];
                }
                ans += (long) (array[i] + last) * cnt >> 1;
                m -= cnt;
            }
        }
        ans += (long) m * x;
        System.out.println(ans);
    }
 
    // 最后一次加攻击力不能到 x
    public static boolean check(int x) {
        int cnt = 0;
        for (int i = 0; i < n; i++) {
            if (array[i] < x) continue;
            cnt += (array[i] - x) / facts[i] + 1;
            if (cnt >= m) return true;
        }
        return false;
    }
 
    public static String next() {
        while (!tokenizer.hasMoreTokens()) {
            try {
                tokenizer = new StringTokenizer(br.readLine());
            } catch (IOException e) {
                e.printStackTrace();
            }
        }
        return tokenizer.nextToken();
    }
 
    public static int nextInt() { return Integer.parseInt(next()); }
 
    public static long nextLong() { return Long.parseLong(next()); }
}

python代码

def check(mid):                          #最后一次技能升级，最多能不能到mid
    cnt = 0 
    for i in range(n):    
        if a[i] < mid:  continue         #第i个技能的初值还不够mid，不用这个技能
        cnt += (a[i] - mid) // b[i] + 1  #第i个技能用掉的次数
        if cnt >= m:   return True       #所有技能升级总次数大于等于m次，说明mid设小了
    return False                         #所有技能升级总次数小于m次，说明mid设大了
 
n, m = map(int, input().split())
a = []                                   #存ai
b = []                                   #存bi
for i in range(n):
    a_,b_ = map(int,input().split())
    a.append(a_)
    b.append(b_)
L,R = 1,1000000                          #二分枚举最后一次攻击力最高能加多少
while(L <= R):
    mid = (L + R) // 2
    if check(mid): L = mid + 1           #增加mid
    else:          R = mid - 1           #减小mid
attack = 0
cnt = m
for i in range(n):
    if a[i] < R:  continue
    t = (a[i] - L) // b[i] + 1               #第i个技能升级次数
    if a[i] - b[i] * (t - 1) == R:  t -= 1   #这个技能每次升级刚好等于R，其他技能更好
    attack += (a[i] * 2 - (t - 1) * b[i]) * t / 2  
    cnt -= t
print(int(attack) + cnt * R)