特征值求解——重启Arnoldi方法和收缩（deflation）技术

重启Arnoldi方法和收缩（deflation）技术

在arnoldi过程中，需要特别注意已经收敛的eigenpairs。

locking策略：已收敛的特征对不再被改动。

假设在某次arnoldi过程中，已经有k个特征对收敛了，Vm写为如下形式：

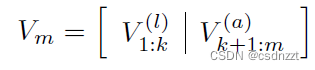
其中上标()表示locked vecotors，上标()表示active vectors。

在下一次的arnoldi过程中，只有m-k个arnoldi向量被计算，也就是active vectors。前k个向量需要被收缩（deflated）。

注意上面两个算法的区别，Algorithm 2相比1唯一的不同是，循环是从k+1开始的，也就是只改变Vm和Hm的最后m-k列，即active部分。

下面是显示重启Arnoldi方法：

通过，Arnoldi向量转换为Schur向量，注意，只作用在新近收敛的向量和下一个初始向量上。随着迭代的进行，k越来越大，当达到预定收敛个数时（k>=nev），?和?构成A的部分Schur分解。

附录：

对于任意k个特征值，都存在一个Schur分解使得这k个特征值出现在R的前k个对角元素，我们将这个R的子矩阵取出来记为Rk，对应的Q中的前k列取出来记为Qk，那么我们有

这个也被称为部分Schur分解（partial Schur decomposition）。注意，S≡Range(Qk)是A的不变子空间，对应着k个特征值，Qk的列是这个子空间的正交基，也被称为Schur基。?重启Arnoldi方法就是被设计用来计算部分Schur分解