MATLAB - 机翼摇摆过程中飞机的模型参考自适应控制

发布时间：2024年01月18日

系列文章目录

前言

本例说明如何控制三角翼飞机在机翼摇晃时的横滚和横滚速率。在本例中，系统模型是未知的。因此，需要使用模型参考自适应控制 (MRAC) 使控制系统与理想参考模型相匹配。飞机在 Simulink? 中建模，MRAC 控制器使用 Simulink Control Design? 软件提供的模型参考自适应控制模块实现。

一、翼摇控制系统

翼摇是三角翼飞机在低速高攻角飞行时出现的一种现象。飞机会出现不期望的滚转振荡，使飞行员更难控制飞机。MRAC 控制器的目标是消除不期望的滚转振荡。然后，您可以设计一个基线控制器来实现所需的参考行为。

以下方程定义了翼摇模型的动力学特性。

$\begin{array}{l l}{?{\dot{\theta}=p}}&{?{\mathrm{}}}\\ {?{p=\Delta(x)+L_\delta\delta_{a}\mathrm{}}}&{?{\mathrm{}}}\\ {?{\dot{\theta}=\Delta(x)+w_{1}^{\star}\theta+w_{2}^{\star}p+w_{3}^{\star}|{\boldsymbol{\rho}}|{\boldsymbol{\rho}}+w_{1}^{\star}|{\boldsymbol{p}}|{\boldsymbol{p}}+w_{5}\theta^{3}}}\end{array}$

这里

x=(θ ,p) 是系统状态向量，其中 θ 是滚动角，p 是滚动率。
$\delta_{a}$ 是飞机副翼角度控制输入。
$L \delta$ ??是控制有效矩阵，您至少知道其符号。
Δ(x) 是翼摇扰动。
$w_i^*$ 是未知的理想权重。

对于这个不确定的非线性系统，您的目标是设计一个控制器，使系统能够跟踪以下二阶参考模型。

$\ddot{x}_{m}=-4x_{m}-2\dot{x}_{m}+4r(t)$ ?

这里

$x_m$ 是参考模型状态向量。
r(t) 是飞行员提供的滚转参考信号。

二、名义模型和参考模型

为滚动动力学指定以下简化的二阶标称模型。

A = [0 1; 0 0]; % Second integrator model
B = [0;1];      % Nominal control effective matrix

?将参考模型定义为之前定义的稳定二阶系统。控制器调整其不确定性模型，以实现与该模型相同的二阶行为。

Am = [0 1; -4 -2]; % Second intergrator model
Bm = [0;4];       % Nominal control effective matrix

指定标称模型和参考模型的初始条件。

theta_0 = 0;   % Initial roll angle (rad)
p0 = 0;        % Initial roll rate (rad/s)
xm = [0;0];    % Initial condition of the reference plant model

三、模型参考自适应控制结构

MRAC 控制器的目标是实现跟踪误差 $e(t)=x(t)-x_m(t)$ 的渐近收敛。

$\lim_{t\to\infty}(x(t)-x_m(t))\to0$

MRAC 控制器的结构如下

$u(t)=-k_x x(t)+k_rr(t)-u_{ad}$ ?

这里

k x 包含反馈控制增益。
k r 包含前馈控制增益。
u ad 是一个自适应控制项，用于消除模型的不确定性。

模型参考自适应控制模块调整自适应控制项，以实现所需的参考模型跟踪。您还可以选择调整反馈和前馈控制增益。不过在本例中，控制增益是静态的。

翼摇系统的静态反馈和前馈控制增益的计算满足以下模型匹配条件。

$\begin{aligned}Am&=A-Bk_x\\Bm&=Bk_r\end{aligned}$ ?

?指定计算出的控制器增益。

Kx = [-4 -2];   % Feedback gain
Kr = 4;         % Feedforward gain

四、不确定性估计参数

MRAC 控制器在线估计模型的不确定性，并生成自适应控制动作 $u_{ad}$
?以消除不确定性，从而恢复基线控制器的标称系统。自适应控制项使用以下模型对系统不确定性进行建模。

$u_{ad}=\mathbf{w}^T\phi(x)$

此处

w 包含由控制器调整的网络权重。
$\phi(x)$ ?是不确定性模型特征向量。

使用模型参考自适应控制模块，可以选择以下特征向量定义之一。

系统状态，其中 ?(x)=x(t) - 这种方法是最简单的选择，如果不知道系统不确定性的复杂程度，这可能是一个很好的起点。如果发现使用状态作为特征并不能充分反映非线性不确定性，则应选择其他方法之一。
具有高斯核的径向基函数 (RBF)、 $\phi(x)=\left[\exp\left(-\dfrac{(x-c_i)^2}{\sigma_i}\right)\right]_{i=1}^N$ ，您可以通过定义特征中心 $c_i$ 和带宽 $\sigma _i$ .
单隐层（SHL）神经网络，隐层神经元数量可指定。
由可选输入端口提供的自定义功能。

在本例中，您将配置控制器使用所有三种方法并比较结果。

定义模型估计学习率 gamma_w 和跟踪误差权重 Q。

gamma_w = 100;   % Learning rate
Q = 1;           % Tracking error weight

?指定径向基函数核的参数。一般来说，配置 RBF 中心时要考虑系统可能的状态空间和带宽，以使核之间有足够的重叠。

N = 10;         % Number of RBF kernels
cen_max = 2;    % Upper limit for kernel centers 
cen_min = -2;   % Lower limit for kernel centers
bandwidth = 25; % Kernel bandwidth

五、使用状态特征向量模拟控制器

打开翼摇控制系统的 Simulink 模型，将系统状态配置为不确定性模型特征向量。

mdl = "wingrockStates";
open_system(mdl)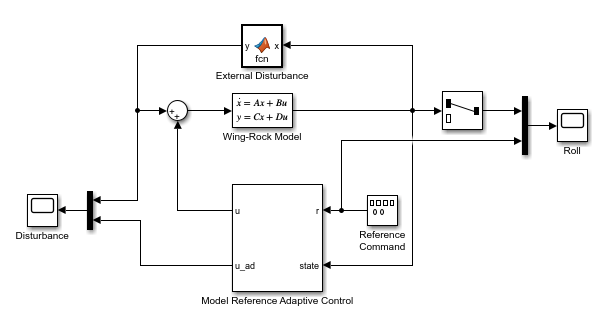

在该模型中

翼摇模型块实现了滚动动力学的标称模型。
外部扰动块生成滚转动力学的翼摇扰动。
参考指令模块生成先导参考信号。
模型参考自适应控制模块输出控制动作 $u_{ad}$ 是翼摇扰动的估计值。

设置模拟持续时间并模拟模型。

Tf = 40;    % Simulation duration (s) 
sim(mdl);

?将飞机滚动结果与参考指令进行比较。

open_system(mdl + "/Roll")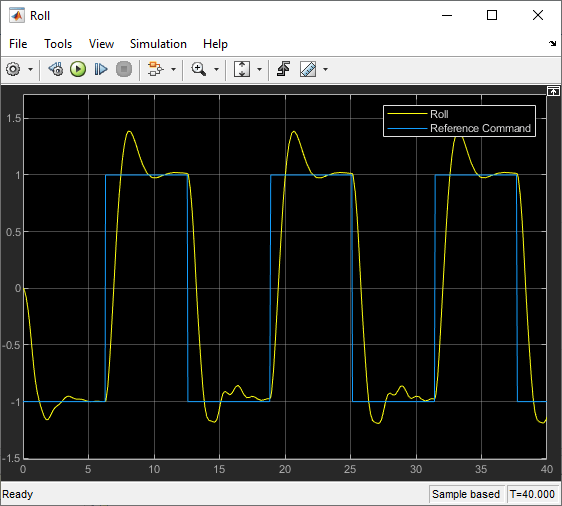

控制器无法实现平滑的二阶瞬态响应。

将 MRAC 控制器估计的扰动模型与真实扰动信号进行比较。

open_system(mdl + "/Disturbance")

当使用状态作为扰动模型特征时，控制器估计的线性扰动模型并不能准确代表真实的非线性扰动。

六、使用 RBF 特征向量模拟控制器

打开配置为使用非线性 RBF 作为不确定性模型特征向量的翼岩控制系统 Simulink 模型。除控制器参数已更新外，该模型与之前的模型完全相同。

mdl = "wingrockSHL";
open_system(mdl)

?仿真模型。

sim(mdl);

查看由此产生的控制器性能。

open_system(mdl + "/Roll")

控制器可对参考指令的变化做出更平滑的二阶响应。

将使用径向基函数估计的扰动与真实扰动进行比较。

open_system(mdl + "/Disturbance")

非线性特征向量可使控制器更准确地估计真实的非线性干扰。

七、使用 SHL 神经网络特征向量模拟控制器

打开配置为使用 SHL 神经网络输出作为不确定性模型特征向量的翼岩控制系统 Simulink 模型。该模型与之前的模型完全相同，只是更新了控制器参数。

mdl = "wingrockSHL";
open_system(mdl)

仿真模型。

sim(mdl);

查看由此产生的控制器性能。

open_system(mdl + "/Roll")

控制器可对参考指令的变化做出平滑的二阶响应。

将使用 SHL 神经网络估算的扰动与真实扰动进行比较。

open_system(mdl + "/Disturbance")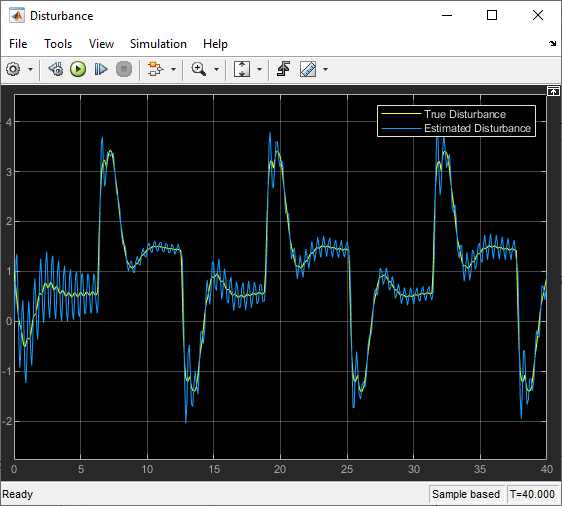

与 RBF 特征向量相比，神经网络近似器计算出的非线性特征向量更接近真实干扰。神经网络参数的配置也更简单。

八、使用自定义特征向量模拟控制器

打开翼摇控制系统的 Simulink 模型，配置为使用外部生成的自定义不确定性模型特征向量。如果您知道干扰和不确定性模型的结构，就可以使用该选项。在本例中，特征模块生成的特征向量与外部干扰模块中使用的特征向量相匹配。

mdl = "wingrockCustom";
open_system(mdl)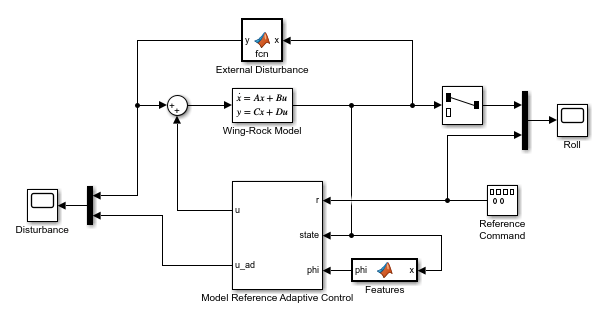

仿真模型。?

sim(mdl);

查看由此产生的控制器性能。

open_system(mdl + "/Roll")

控制器可对参考指令的变化做出更平滑的二阶响应。

将使用自定义特征向量估计的干扰与真实干扰进行比较。

open_system(mdl + "/Disturbance")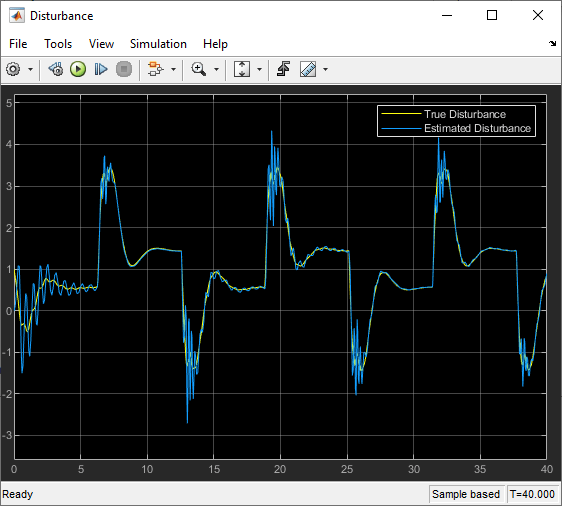

不出所料，使用基于扰动行为先验知识的自定义特征向量可以生成更准确的真实扰动模型。

文章来源:https://blog.csdn.net/weixin_46300916/article/details/135554516
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！