混合高斯模型的应用与理解

混合高斯模型数学表达

混合高斯模型是一种概率模型，用于对包含多个高斯分布的数据进行建模。在混合高斯模型中，假设观测数据是由多个高斯分布组合而成的，每个高斯分布称为一个分量。每个观测数据点都由这些分量中的某一个生成，但具体是哪一个分量生成的则是不可观测的隐变量。

混合高斯模型的核心在于其对数据的概率密度函数的建模方式。模型的数学表示如下：

其中，P(X) 是观测数据的概率密度函数，πk? 是第 k 个分量的权重，N(X∣μk?,Σk?) 是多元高斯分布，μk? 和 Σk? 分别是第 k 个分量的均值和协方差矩阵。整个混合高斯模型的概率密度函数表示了对每个分量进行加权的总和，每个分量对应一个高斯分布，权重表示了每个分量在总体概率分布中的相对贡献。并且权重满足

核心参数及应用

混合高斯模型有一些核心参数，它们定义了模型的特征和行为。以下是混合高斯模型的主要核心参数：

• 均值（Means）： 对应于每个高斯分量的均值向量。每个分量都有一个均值，表示该分量在每个特征上的中心位置。
• 协方差矩阵（Covariance Matrices）： 对应于每个高斯分量的协方差矩阵。协方差矩阵描述了每个分量在不同特征上的变化关系，它反映了数据的形状和方向。
• 权重（Weights）： 每个高斯分量的权重，表示该分量在整个混合模型中的相对贡献。权重是非负的且总和为1。

这三个参数定义了混合高斯模型的外观和性质。通过调整这些参数，可以控制模型对数据的拟合程度，从而更好地适应不同类型的数据分布。混合高斯模型在数据建模和分析中有许多重要的应用，其中一些包括：

• 聚类（Clustering）： 混合高斯模型可以用于对数据进行聚类，即将数据分成不同的组，每个组对应于混合模型中的一个分量。每个分量代表了一个簇，这种方法尤其适用于数据集中存在多个潜在的子群体的情况。
• 密度估计： 混合高斯模型可以用于估计数据的概率密度函数。通过对每个分量的高斯分布进行加权和，模型能够更准确地捕捉数据的复杂分布，尤其是当数据包含多个模态（多个峰值）时。
• 异常检测： 混合高斯模型可以用于检测数据中的异常点。通过估计正常数据的分布，模型可以识别偏离这个分布的观测值作为异常。
• 生成模型： 混合高斯模型可用于生成新的样本。一旦模型参数被学习，可以通过对分量进行随机采样来生成符合模型分布的新数据。
• 图像分割： 在图像处理中，混合高斯模型经常用于分割图像中的不同区域。每个分量对应于图像中的一个区域，通过对图像中每个像素的分类，可以实现图像分割。

MATLAB例子说明

可视化混合高斯模型的概率密度函数

% 设置随机种子以确保结果可重复
rng(1);

% 定义混合高斯模型参数
mu1 = [2; 2];
Sigma1 = [1, 0.5; 0.5, 2];
pi1 = 0.6;

mu2 = [-2; -2];
Sigma2 = [1, -0.8; -0.8, 2];
pi2 = 0.4;

% 生成混合高斯模型
gm = gmdistribution([mu1, mu2], cat(3, Sigma1, Sigma2), [pi1, pi2]);

% 生成观测数据
X = random(gm, 500);

% 可视化观测数据
figure;
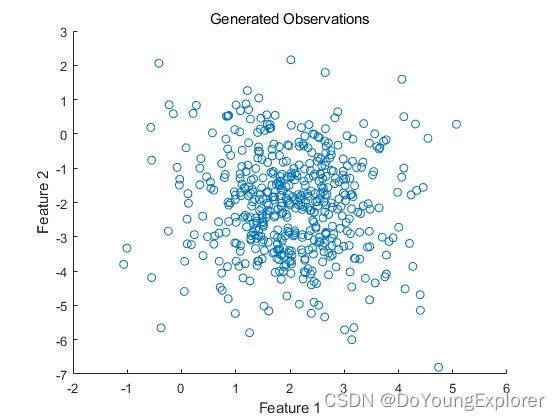
scatter(X(:, 1), X(:, 2), 'o');
title('Generated Observations');
xlabel('Feature 1');
ylabel('Feature 2');

% 绘制混合高斯模型的等高线图（概率密度函数）
figure;
ezcontour(@(x, y) pdf(gm, [x, y]), [-8, 8], [-8, 8]);
title('Probability Density Function (PDF) of Mixture Gaussian Model');
xlabel('Feature 1');
ylabel('Feature 2');

解释说明：

• 随机种子设置： rng(1) 设置随机数生成器的种子，以确保每次运行代码时生成的随机数相同，保证结果的可重复性。
• 定义混合高斯模型参数： 定义两个高斯分量的均值 mu1、mu2，协方差矩阵 Sigma1、Sigma2，以及它们的权重 pi1、pi2。
• 创建混合高斯模型： 使用 gmdistribution 函数创建混合高斯模型对象 gm，其中指定均值、协方差矩阵和权重。
• 生成观测数据： 使用 random 函数生成符合混合高斯模型分布的观测数据 X。
• 绘制概率密度函数： 使用 ezcontour 函数绘制混合高斯模型的概率密度函数等高线图，其中 pdf(gm, [x, y]) 计算给定坐标 (x, y) 处的概率密度。

通过这个示例，我们能够可视化混合高斯模型的概率密度函数，从而更好地理解模型对数据的拟合效果。

聚类应用：

混合高斯模型可以用于聚类，特别是在数据集中包含多个潜在的分组时。下面是一个简单的示例，演示如何使用混合高斯模型对数据进行聚类：

% 生成包含三个簇的数据
rng(1);  % 设置随机种子
data = [mvnrnd([1, 1], eye(2), 100); mvnrnd([5, 5], 0.5 * eye(2), 100); mvnrnd([9, 1], eye(2), 100)];

% 使用混合高斯模型进行聚类
numClusters = 3;
gm = fitgmdist(data, numClusters);

% 预测每个数据点所属的簇
clusterIdx = cluster(gm, data);

% 可视化聚类结果
figure;
scatter(data(:, 1), data(:, 2), 30, clusterIdx, 'filled');
title('Clustering with Gaussian Mixture Model');
xlabel('Feature 1');
ylabel('Feature 2');
% 提取混合高斯模型的均值、协方差矩阵和权重
mu = gm.mu;           % 均值
sigma = gm.Sigma;     % 协方差矩阵
weights = gm.ComponentProportion;  % 权重

% 显示均值
disp('均值:');
disp(mu);

% 显示协方差矩阵
disp('协方差矩阵:');
disp(sigma);

% 显示权重
disp('权重:');
disp(weights);

% 提取混合高斯模型的均值、协方差矩阵和权重
mu = gm.mu;           % 均值
sigma = gm.Sigma;     % 协方差矩阵
weights = gm.ComponentProportion;  % 权重

% 设置图形大小
figure('Position', [100, 100, 1000, 400]);

% 绘制每个分量的椭圆（二维情况）并标记均值
for i = 1:numClusters
    subplot(1, numClusters, i);
    
    % 绘制椭圆轮廓
    ezcontour(@(x, y)mvnpdf([x, y], mu(i, :), squeeze(sigma(:, :, i))), [-5, 15], [-5, 15]);
    
    hold on;
    
    % 散点表示观测数据
    scatter(data(:, 1), data(:, 2), 20, 'k', 'filled', 'MarkerFaceAlpha', 0.3);
    
    % 标记均值
    scatter(mu(i, 1), mu(i, 2), 100, 'r', 'filled');
    
    % 设置坐标轴范围，使得图形充满整个子图
    axis equal;
    xlim([-5, 15]);
    ylim([-5, 15]);
    
    % 设置标题
    title(['Component ', num2str(i)]);
    
    % 设置坐标轴标签
    xlabel('Feature 1');
    ylabel('Feature 2');
    
    hold off;
end

均值:
    0.9515    0.9619
    5.0985    4.9777
    9.0221    0.9296

协方差矩阵:

(:,:,1) =

    0.9804   -0.1132
   -0.1132    0.9648


(:,:,2) =

    0.3879    0.0519
    0.0519    0.4591


(:,:,3) =

    1.4675   -0.0326
   -0.0326    0.8761

权重:
    0.3333    0.3334    0.3333

解释说明：

• mvnrnd: 生成多元正态分布的随机样本。
• fitgmdist: 返回一个包含拟合结果的混合高斯模型对象 gm。该对象包括了估计出的混合高斯分布的均值、协方差矩阵、权重等信息。
• cluster: 函数返回一个向量 modeIdx，其中的每个元素表示对应观测数据点所属的混合分量的索引。这个索引即代表了数据点所属的聚类。

此示例生成包含三个簇的二维数据，并使用混合高斯模型拟合数据。通过 cluster 函数预测每个数据点所属的簇，并通过散点图可视化聚类结果。

这两个示例突显了混合高斯模型在聚类中灵活性和应用价值。混合高斯模型能够对复杂的数据结构进行建模，并为每个数据点分配概率。在实际应用中，可根据具体问题调整混合高斯模型的参数，以满足不同场景的需求。