多标签节点分类

Multi-Label Node Classification on Graph-Structured Data,TMLR’23
Code
学习笔记

图结构数据的多标签分类

1. 节点表示或嵌入方法
   通常会生成查找表，以便将相似的节点嵌入的更近。学习到的表示用作各种下游预测模块的输入特征。
   表现突出的方法是基于随机游走(random walk)的方法：通过节点在随机游走中的共现频率(co-occurrence frequency)来定义节点之间的相似性。[在随机游走的过程中，如果两个节点经常在一起出现，即它们在游走序列中共现的频率较高。]比如DeepWalk

2. CNN.其他方法比如说使用卷积神经网络，首先通过聚合局部邻域的特征信息来提取节点表示。然后将提取的特征向量与标签嵌入融合以生成最终的节点嵌入。比如LANC

3. 图神经网络(GNNs)
   通过递归聚合和转换其邻居的特征表示来计算节点表示，然后将其传递到分类模块。图卷积运算的第k层可以描述为：
   $z_i^{(k)}=AGGREGATE(\left\{{\mathbf{x}}_i^{(k?1)},\left\{{\mathbf{x}}_j^{(k?1)}|j\in N(i)\right\}\right\})$
   对于多标签节点分类，采用sigmoid层作为最后一层来预测类别概率：$\mathbf{y}\leftarrow (\text{sigmoid}(z_i^{(L)}\theta ))$ $\theta$对应于分类模块中的可学习权重矩阵。
   GNN模型的主要区别在于聚合层的实现。最简单的模型是GCN：对邻域特征采用度加权（degree-weighted）聚合；
   GAT采用了多个堆叠的图注意力层，它允许节点关注其邻域的特征；
   GraphSAGE仅使用邻域的随机样本进行特征聚合步骤。
   一般来说，GNNs在高**同配图（连接的节点往往共享相同的标签）**表现出更好的性能。H2GCN显示了在异配图上（多类设置）的改进：将邻居聚合的信息与自我节点的信息分开。此外，它利用高阶邻域信息来学习信息丰富的节点表示。

4. 标签传播（label propagation）
   LPA算法和GNNs都基于消息传递。GNNs传播和变换节点特征，而LPA沿着图的边缘传播节点标签信息，以预测未标记节点的标签分布。 最近的一些工作将他们结合起来，比如GCN-LPA利用LPA作为正则项来帮助GCN学习适当的边权重，从而提高分类性能。

多标签数据集的特性

标签同配性label homophily

本文提出多标签图数据集的同配性定义
GNNs的性能通常根据标签同配性来讨论，标签同配性量化了图中相似节点之间的相似性，特别是，标签同配性在文(Beyond homophily in graph neural networks: Current limitations and effective designs)中被定义为图中同配边的分数：其中如果一条边连接具有相同标签的两个节点，则该边被认为是同配的。
这一定义不能直接用于多标签图数据集，因为每个节点可以有多个标签，并且在多标签dataset中两个连接节点的整个标签集相同的情况很少见。通常，两个节点共享其部分标签。
给定一个多标签图$G$，其同配性$h$定义为图中所有连通节点的标签集的杰卡德（Jaccard）相似度的平均值：
$$h=\frac{1}{|\epsilon |}\sum _{(i,j)\in \epsilon }\frac{|l(i)\cap l(j)|}{|l(i)\cup l(j)|}.$$
标签同配性是一阶标签引起的相似性，因为它根据相邻节点的标签分布来量化相邻节点之间的相似性。

跨类邻域相似度CCNS

二阶标签诱导度量，量化任何两个节点的邻域之间的相似性。

异配图的CCNS较低，同配图的CCNS更高

常用多标签节点分类数据集

1. BlogCat
   nodes博客作者，edges表示他们的关系，labels表示所属社会群体
2. Yelp
   nodes客户评论，edges对应他们的friendship，labels代表企业类型
3. OGB-Proteins
   nodes蛋白质，edges表示蛋白质之间不同类型的生物学意义关联，labels对应于蛋白质功能
4. DBLP
   nodes作者，edges合著关系，labels表示作者的研究领域

‘25%’、'50%'和’75%'对应于节点的标签数量的排序列表的第25、第50和第75位。即，有 25%、'50%‘或’75%’ 的节点的标签数目小于或等于这个值。

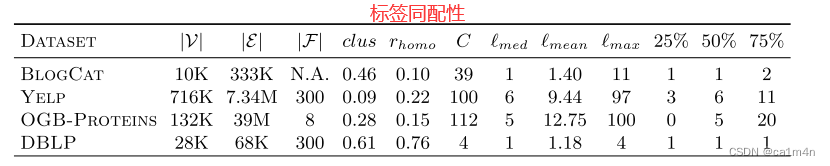
• 标签分布不对称
• 高标签稀疏性下使用AUROC评分进行评估存在问题
  （ROC曲线是以召回率为纵轴，FPR为横轴的曲线，其面积代表AUROC分数
  FPR是被错误地预测为正类别地负样本占所有负样本的比例，召回率是预测为true positive样本占所有实际positive样本的比例）
  因此存在，通过增加训练使其的数量来增加AUROC分数，即鼓励了模型通过预测为negative样本来减少损失。

NEW生物数据集

1. PCG：蛋白质表型预测（phenotype：疾病可观察到的特征或形状）
2. HumLoc：人类蛋白质亚细胞位置预测数据集（预测蛋白质亚细胞位置可以帮助识别药物靶点）标签是位置信息，14个维度one-hot编码
3. EukLoc：真核生物蛋白质亚细胞位置预测数据集
   
   HUMLOC、EUKLOC有着较高的同配性

Results

---

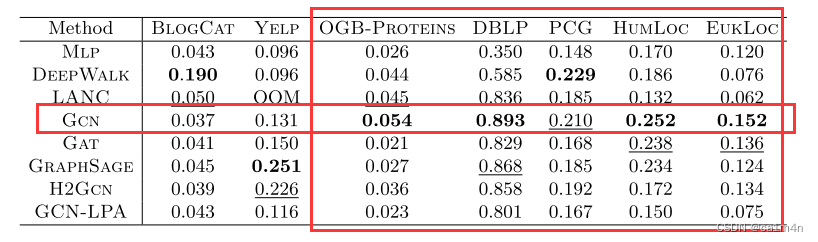
1. DBLP
2. EukLoc
3. HumLoc
4. PCG