【回溯算法】n-皇后
发布时间:2024年01月08日
题目来源
题目描述
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的n 皇后问题的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中'Q' 和 '.'分别代表了皇后和空位。
示例
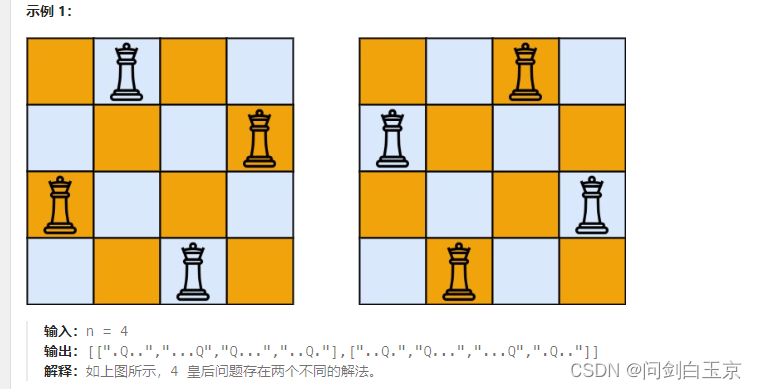
思路
这道题是根据
labuladong算法秘籍刷到的
回溯的过程可以看作是决策树中做决策与撤回决策,决策就是走向下一层,撤回决策就是返回。

核心代码:
void backtrack(当前选择, 剩余选择列表) {
if (当前选择产生的结果满足结束递归条件) {
return;
}
for (选择 in 剩余选择列表) {
//做出当前选择
st[选择] = true;
// 进入下一层决策树
backtrack(选择 ,剩余选择列表);
// 撤回选择
st[选择] = false;
}
}
- 在本题中决策树的每一层表示棋盘上的每一行;每个节点可以做出的选择是,在该行的任意一列放置一个皇后。
- 回溯的过程中,当前考虑行的前面所有行已经做过选择
回溯函数
/**
@description: 回溯函数,如果当前递归到row行,前row-1行已经放置好皇后
@param: borad - 棋盘
@param: row - 当前到第几行了
*/
void backtrack(vector<string> &borad, int row) {
if (row == borad.size()) {
res.push_back(borad);
return;
}
int n = borad[row].size();
for (decltype(borad.size()) i = 0; i < n; ++ i) {
// 判断row 行 i 列可不可以放皇后
if (!valid(borad, row, i)) {
// 不能放
continue;
}
// 放置皇后
borad[row][i] = 'Q';
// 继续下一行棋盘
backtrack(borad, row + 1);
// 不放
borad[row][i] = '.';
}
}
valid函数用于判断当前位置是否可以放置皇后:
如果当前位置所在行、列、正对角线、负对角线有放置皇后,那么当前位置就不可以放置皇后了
valid函数
/**
@param: board 棋盘
@param: row 行
@param: line 列
@return bool类型,true表示可以放,false表示不可以放
*/
bool valid(vector<string> &board, int row, int line) {
int n = board.size();
// 同一行是否放了皇后
for (int j = 0; j < line; ++ j) {
if (board[row][j] == 'Q') return false;
}
// 同一列是否放了皇后
for (int i = 0; i < row; ++ i) {
if (board[i][line] == 'Q') return false;
}
// 左斜线是否放了皇后
int b = line - row;
for (int i = 0; i < row; ++i) {
int j = i + b;
if (j < 0) continue;
if (board[i][j] == 'Q') return false;
}
// 右斜线是否放了皇后
b = row + line;
for (int i = 0; i < row; ++ i) {
int j = b - i;
if (j < 0) continue;
if (board[i][j] == 'Q') return false;
}
// 都没有放皇后
return true;
}
这里解释一下为什么正对角、负对角这么计算:将棋盘想象成下面样子
正对角的情况如下:
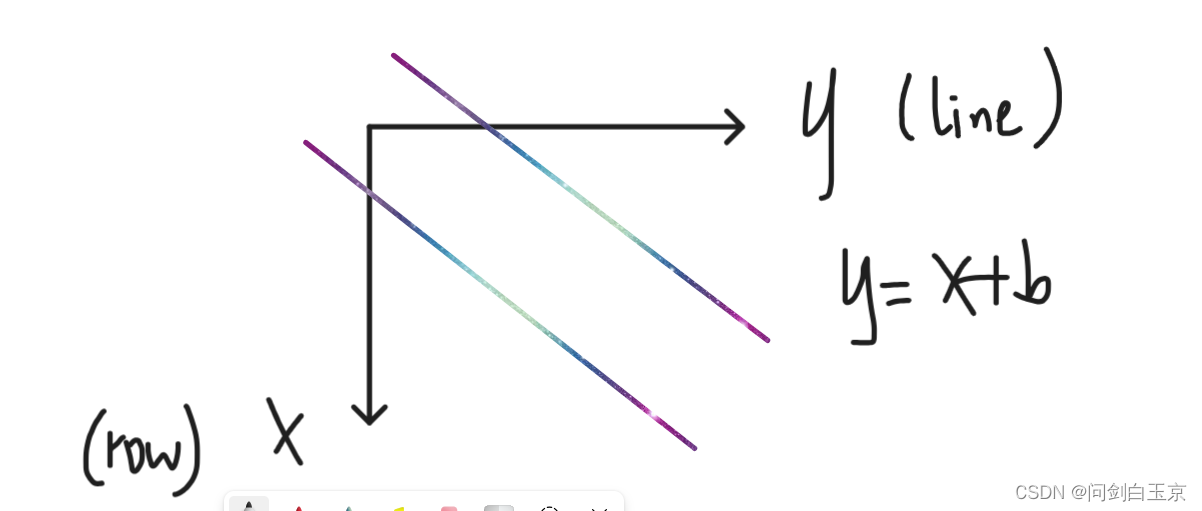
对于当前位置(row, line),我们可以确定这条对角线:计算b = y - x;
所以b = line - row, 然后从 0 ~ row - 1 计算每一个 y值, 然后要保证y值为正
负对角同理
完整代码
class Solution {
public:
vector<vector<string>> res;
vector<vector<string>> solveNQueens(int n) {
vector<string> borad(n, string(n, '.'));
// 回溯
backtrack(borad, 0);
return res;
}
/**
@description: 回溯函数,如果当前递归到row行,前row-1行已经放置好皇后
@param: borad - 棋盘
@param: row - 当前到第几行了
*/
void backtrack(vector<string> &borad, int row) {
if (row == borad.size()) {
res.push_back(borad);
return;
}
int n = borad[row].size();
for (decltype(borad.size()) i = 0; i < n; ++ i) {
// 判断row 行 i 列可不可以放皇后
if (!valid(borad, row, i)) {
// 不能放
continue;
}
// 放置皇后
borad[row][i] = 'Q';
// 继续下一行棋盘
backtrack(borad, row + 1);
// 不放
borad[row][i] = '.';
}
}
/**
@param: board 棋盘
@param: row 行
@param: line 列
@return bool类型,true表示可以放,false表示不可以放
*/
bool valid(vector<string> &board, int row, int line) {
int n = board.size();
// 同一行是否放了皇后
for (int j = 0; j < line; ++ j) {
if (board[row][j] == 'Q') return false;
}
// 同一列是否放了皇后
for (int i = 0; i < row; ++ i) {
if (board[i][line] == 'Q') return false;
}
// 左斜线是否放了皇后
int b = line - row;
for (int i = 0; i < row; ++i) {
int j = i + b;
if (j < 0) continue;
if (board[i][j] == 'Q') return false;
}
// 右斜线是否放了皇后
b = row + line;
for (int i = 0; i < row; ++ i) {
int j = b - i;
if (j < 0) continue;
if (board[i][j] == 'Q') return false;
}
// 都没有放皇后
return true;
}
};
文章来源:https://blog.csdn.net/weixin_47466118/article/details/135465782
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- [框架系列]-[通用lock框架]集成及具体配置使用
- 【js判断移动端和pc端】【js判断是否是ipad(兼容ios13)】
- Redis高并发分布式锁
- 双指针算法专题
- Element - ui :el-input 输入只能是数字并且小数点后只能是1-2位
- 线性代数——(期末突击)行列式(上)-行列式计算、行列式的性质
- 完全备份、增量备份、差异备份、binlog日志
- 【map坑点】原始数组为空,有两种操作:1、在数组后面添加元素x 2、复制x个原始数组添加在原始数组后面。q次询问,求第k(k <= 1e18)个元素是什么
- springboot+vue+java+mysql 铁路订票管理系统 原创
- React和Vue的生态系统有何不同?
