树低级（C语言版）

发布时间：2023年12月31日

一.树基本计算规则

关于树的大部分知识点我们都讲过了，那么如果我给你树的节点，你可以算出叶子节点个数吗？

下面我们总结下一些计算规则：

1.父子计算规则：

parent=(child-1)/2;

leftchild=parent*2+1,rightchild=parent*2+2;

2.若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)个节点

3.深度为h的二叉树的最大结点数是2^h-1;

4. 对任何一棵二叉树, 如果度为0其叶结点个数为N0?, 度为2的分支结点个数为N2 ,则有

N0＝N2＋1
5. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=log（n+1)? (log以2 为底，n+1为对数)
例题一：
1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为
A 不存在这样的二叉树
B 200
C 198
D 199
规则4，结果为200个，即B
如果不知道规则，那么就可能浪费不必要的时间，大家可以自行去找其他题目。

二.层序遍历

上次我们留下层序遍历没实现，现在我们学习树更近一步了，我们可以实现层序遍历了，在实现前让我们来看看下面两个概念：
深度优先遍历（Depth First Search)：简称DFS，前序遍历，中序遍历和后序遍历都是,即一种 递归的遍历方式， 从一个起点开始，沿着一条路径一直走到底，直到不能再走为止，然后回溯到上一个节点，继续遍历其他路径，直到所有节点都被遍历过。
广度优先遍历（Breadth First Search)：又称为广度优先搜索，简称BFS。是一种分层的查找过程，每向前走一步可能访问一批顶点，不像深度优先搜索那样有往回退的情况，因此它不是一个递归的算法。它是一个逐层遍历的过程，层序遍历就是BFS。
大家可能都经历过这样一个过程，就是使用QQ时，会推荐好友的好友，这其实就是一个广度优先遍历的实例。
下面回归我们主题：
如何去写层序遍历呢？
这个时候，是不是可以想到用队列，如果我们将树根放进队列，如果我们出队列，将树根的左右子序列放入，这样一直循环，是不是就可以做到层序遍历。
下面请看代码： 
// 层序遍历定义(一：一起遍历）
void LevelOrder(TreeNode* root)
{
	Queue s1;
	QueueInit(&s1);
	//判断是否为空，不空的话，先压进一个
	if(root)
		QueuePush(&s1, root);
	while (!QueueEmpty(&s1))
	{
		TreeNode* cur = QueueFront(&s1);
		QueuePop(&s1);
		printf("%d ", cur->date);
		//压入它的左右孩子
		if(root->left)
			QueuePush(&s1, root->left);
		if (root->right)
			QueuePush(&s1, root->right);
	}
	printf("\n");
}

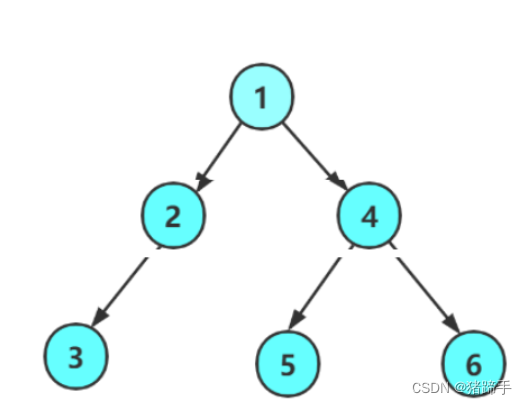
还是以这个树，我们检查一下： 
//动态开辟空间定义
TreeNode* BuyTreeNode(int x)
{
	//开辟树的空间
	TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
	assert(node);
	node->date = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}
//建立二叉树定义
TreeNode* CreateTree()
{
	//开辟树并且对每个进行赋值
	TreeNode* node1 = BuyTreeNode(1);
	TreeNode* node2 = BuyTreeNode(2);
	TreeNode* node3 = BuyTreeNode(3);
	TreeNode* node4 = BuyTreeNode(4);
	TreeNode* node5 = BuyTreeNode(5);
	TreeNode* node6 = BuyTreeNode(6);

	//确定指向
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}
int main()
{
	TreeNode* root = CreateTree();
	LevelOrder(root);
	BinaryTreeDestory1(root);
	root = NULL;
	return 0;
}

结果：

是不是满足了层序遍历，好了，现在如果我让你将每层的结果，一行打印一层结果，该如何写呢？ 
// 层序遍历定义(二：逐层遍历）
void LevelOrder2(TreeNode* root)
{
	Queue s1;
	QueueInit(&s1);
	int size = 1;
	//判断是否为空，不空的话，先压进一个
	if (root != NULL)
		QueuePush(&s1, root);
	while (!QueueEmpty(&s1))
	{
		while (size>0)
		{
			TreeNode* cur = QueueFront(&s1);
			QueuePop(&s1);
			printf("%d ", cur->date);
			//压入它的左右孩子
			if (cur->left)
				QueuePush(&s1, cur->left);
			if (cur->right)
				QueuePush(&s1, cur->right);
			size--;
		}
		printf("\n");
		size = QueueSize(&s1);
	}
	printf("\n");
}

结果：（还是上面的树）

三.判断二叉树是否是完全二叉树

判断一棵树是不是完全二叉树，我们还是可以利用栈来实现，这里很好理解，就直接展示代码了，里面都有注释。 
//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(TreeNode* root)
{
	Queue s1;
	QueueInit(&s1);
	//判断是否为空，不空的话，先压进一个
	if (root != NULL)
		QueuePush(&s1, root);
	//找到第一个空
	while (!QueueEmpty(&s1))
	{
		
		TreeNode* cur = QueueFront(&s1);
		QueuePop(&s1);
		if (cur == NULL)
			break;
		//压入它的左右孩子,注意：不用判断了		
		QueuePush(&s1, cur->left);
		QueuePush(&s1, cur->right);		
	}
	//第二步：如果在栈中还有非空，就说明不是完全二叉树
	//定理：如果不是完全二叉树，那么栈里面此时一定有数据了
	while (!QueueEmpty(&s1))
	{
		TreeNode* cur2 = QueueFront(&s1);
		QueuePop(&s1);
		if (cur2 != NULL)
			return false;
	}
	return true;
}

检查：

//建立二叉树定义
TreeNode* CreateTree()
{
	//开辟树并且对每个进行赋值
	TreeNode* node1 = BuyTreeNode(1);
	TreeNode* node2 = BuyTreeNode(2);
	TreeNode* node3 = BuyTreeNode(3);
	TreeNode* node4 = BuyTreeNode(4);
	TreeNode* node5 = BuyTreeNode(5);
	TreeNode* node6 = BuyTreeNode(6);
	TreeNode* node7 = BuyTreeNode(7);

	//确定指向
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node2->right = node7;
	node4->left = node5;
	//node3->left = node5;
	node4->right = node6;
	return node1;
}

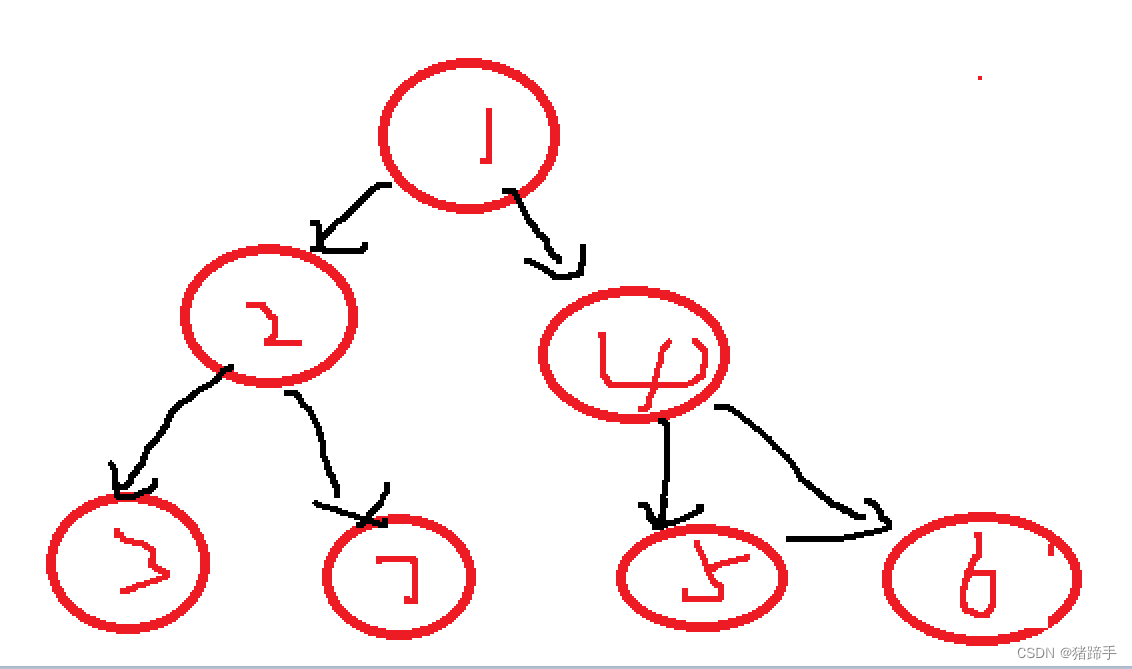
对于这棵树结果为：
当然，你也可以自己去检查我的结果
对于树的中等部分就补充到这里了，后面我们还会讲一些高级的树，元旦快乐，bye！！！
文章来源:https://blog.csdn.net/2301_79813267/article/details/135307431
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章