最小生成树算法

前言

图的最小生成树（MST）是术语“最小权重生成树”的简称。

通常所说的都是无向图的MST。

一般来说有三种比较常见的最小生成树算法：

• 克鲁斯卡尔算法（Kruskal）
• 普利姆算法（Prim）
• 博鲁夫卡算法（Boruvka）
• LCT求MST

一般来说克鲁斯卡尔最短，所以只求MST的话，克鲁斯卡尔完全足够了。

其时间复杂度分别为：

• 克鲁斯卡尔：$O(m\log m)$
• 普利姆：$O(m\log n)$
  使用斐波那契堆优化的普利姆算法可以做到大常数$O(m+n\log n)$
  c++的斐波那契堆可以使用pb_ds
• 博鲁夫卡：$O(m\log n)$

注：由于$m=O(n^2)$，因此$O(\log m)=O(\log n)$，从渐进意义上说，除了斐波那契堆优化的普利姆算法之外，三者的时间复杂度是一样的。

克鲁斯卡尔算法（Kruskal）

克鲁斯卡尔的过程是：

• 把$n$个点看做$n$个连通块
• 不断找出一条连接两个不同连通块的权值最小的边
  • 这条边加入MST，然后把这两个连通块合并为一个
  • 直到图中只有一个连通块

对于算法的正确性，我们可以这样看，首先我们知道全局最小的一条边（可能有多条）一定会包含在至少一个MST之内。否则假设它不在任何一个上，把它的一个临接点原有的边断开，换成这条边，树的权值不会变大，则新树仍为MST，矛盾。

其次，在求MST时，假如说我们选择了一条边$(u,v)$，那么我们就可以把点$u$和点$v$缩成一个新点$x$：

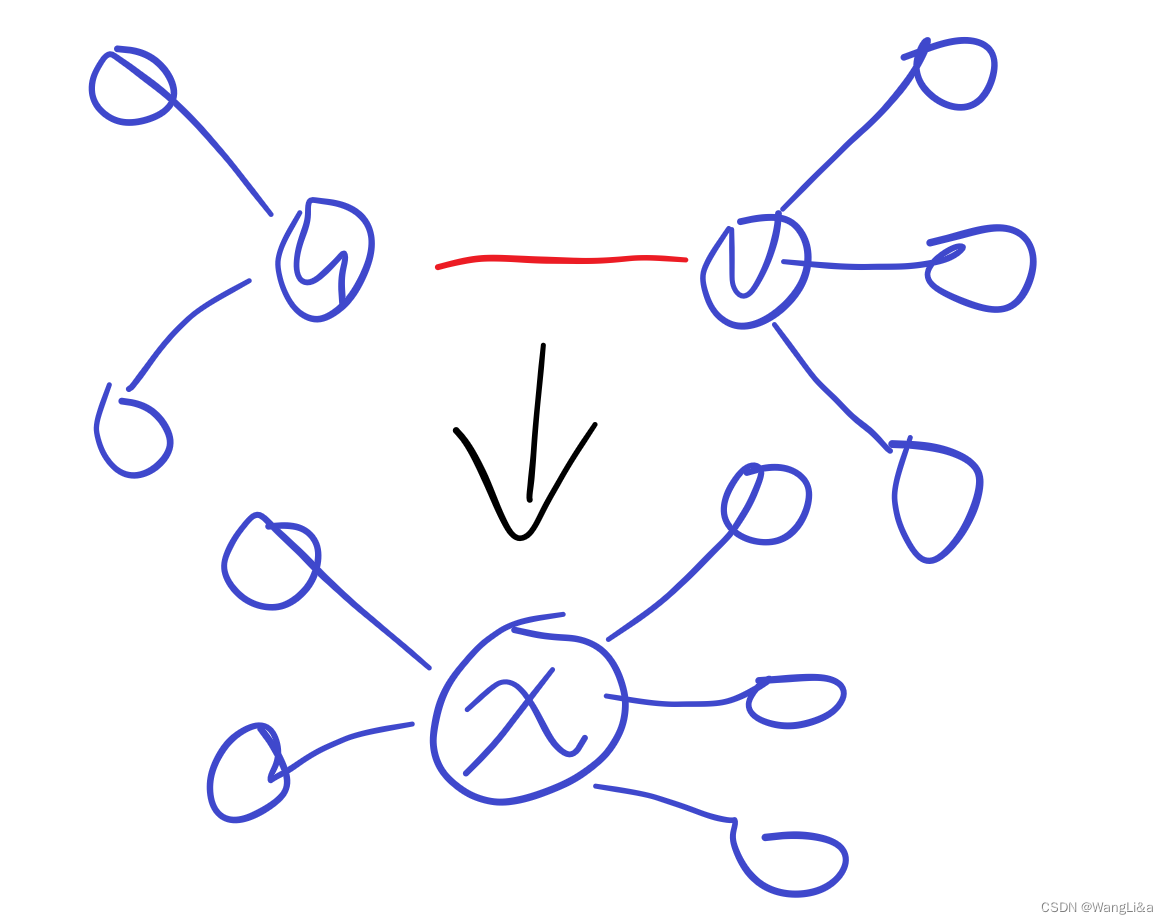
这显然是可以的，因为我们对于 { u , v } \{u,v\} {u,v}这个连通块，外部只能向其再连接一条边了，而且连接的这条边可以是连接到$u$，也可以是$v$，这完全等价于新点$x$继承了$u,v$两点的边。
因此MST等于新图上的MST拼接上原图上$(u,v)$这条边。
（事实上这个论断还是没有严谨证明，但是本文不是应用文章，所以没必要过分严谨）

有了这两个事实，我们可以对点数和边数进行归纳，得到正确性分析。

这已经非常显然了，因此我们不再想写形式化证明。

容易发现，克鲁斯卡尔的过程实际上就是在模拟不断选出全局最小的边+缩点的过程，因此它的正确性是显然的。

我们通常需要用并查集来维护连通性，因此其时间复杂度为$O(m\alpha (n)+m\log m)$。

由于我们事实上不需要实现复杂度为反阿克曼函数的并查集，我们可以只使用路径压缩并查集，其复杂度为$O(m\log n)$

实现

#include<iostream>
#include<algorithm>
#include<climits>
using namespace std;
const int N=2e5;
int fa[N+5];
int find(int u){
	return fa[u]^u?find(fa[u]):u;
}
void merge(int x,int y){
	fa[find(x)]=fa[find(y)];
}
int n,m;
struct edge{
	int u,v,w;
}a[N+5];
int kruskal(){
	sort(a+1,a+1+m,[](edge a,edge b){return a.w<b.w;});
	int sum=0;
	int cnt=0;
	for(int i=1;i<=m;i++) {
		edge x=a[i];
		if(find(x.u)^find(x.v))
			sum+=x.w,merge(x.u,x.v),cnt++;
	}
	if(cnt<n-1) {
		cout<<"orz"<<endl;
		exit(0);
	}
	return sum;
}
int main() {
	cin>>n>>m;
	for(int i=1;i<=n;i++) fa[i]=i;
	for(int i=1;i<=m;i++) cin>>a[i].u>>a[i].v>>a[i].w;
	cout<<kruskal();
} 

普利姆算法（Prim）

普利姆算法的过程是：

• 随意选择一个点，维护这个点的连通块，初始连通块只包含这一个点
• 不断找到连接连通块与连通块外部点的权值最小的边
  • 把这条边加入MST，把连接的点合并到连通块内
  • 直到图中只有一个连通块

普利姆算法的正确性除了应用上文中MST可以“缩点”的事实之外，还有另一个事实：
一定存在某个最小生成树，使得点$u$的邻接边中权值最小的其中一条在这个生成树上。
这也是显然的。否则假设这条边不在任何一个MST上，设这条边为$(u,v)$，然后找到$v$在生成树上到达$u$的路径上抵达$u$的边，然后把它断开，连上$(u,v)$，树权和不会变大，则新树仍为MST，矛盾。

有了这两个事实，我们可以对点数和边数进行归纳，得到正确性分析。

可以使用优先队列来维护连接连通块和外部点中最小的边，具体过程为：

• 随机一个点$x$，把$x$加入集合$S$
• 把$x$的所有邻接边按照边权放入小顶堆
• 取出小顶堆的堆顶
  • 如果堆顶这条边连接的两端都在集合内部：continue
  • 否则把它加入MST，连接的外部点加入集合$S$，再把外部点的邻接边放入堆
  • 直到堆为空

时间复杂度$O(m\log m)$

博鲁夫卡算法（Boruvka）

博鲁夫卡的过程是：

• 把$n$个点看做$n$个连通块
• 每次找到每个连通块连接向外部的边中最小的一个，把这些边加入MST，然后把这些边连接的连通块分别合并
• 直到图中只有一个连通块

博鲁夫卡的正确性也是显然的。
由于合并的过程只会进行$O(\log n)$轮，因此其复杂度为$O(m\log n)$

博鲁夫卡算法是一种在1926年提出的算法，其时间甚至早于发明计算机（1946年），这个算法本来的作用是为了快速寻找最优的电力供应路径。

后记

于是皆大欢喜。