[笔记]深度学习入门 基于Python的理论与实现(一)

1. python 入门

1.5之前是python安装和基础语法, 我直接跳过了

1.5 Numpy

深度学习中经常出现数组和矩阵运算，Numpy 的数组类 numpy.array 提供了很多便捷的方法

1.5.1 导入 Numpy

import numpy as np

1.5.2 生成 Numpy 数组

np.array()，接收 python 列表，生成 Numpy 数组

x = np.array([1.0, 2.0, 3.0])
print(x)
print(type(x))

1.5.3 Numpy 的数学运算

x = np.array([1.0, 2.0, 3.0])
y = np.array([2.0, 4.0, 6.0])

print(x + y)
print(x - y)
print(x * y)
print(x / y)

需要注意，用于计算的数组的元素个数要相同

‘对应元素的’的英文是 element-wise，而 numpy 不仅可以进行 element-wise 运算，还可以和单一的数值（标量）组合起来进行计算。此时，需要在
numpy 数组的各个元素和标量之间进行计算，这个功能也称为广播

x = np.array([1.0, 2.0, 3.0])
print(x / 2.0)

1.5.4 Numpy 的 N 维数组

numpy 可以生成多维数组

A = np.array([[1, 2], [3, 4]])
print(A)
print(A.shape)
print(A.dtype)

shape 可以查看矩阵的形状，dtype 可以查看矩阵元素的数据类型

B = np.array([[3, 0], [0, 6]])
print(A + B)
print(A * B)

矩阵运算可以在相同形状的矩阵间以对应元素的方式进行。也可以通过标量（单一数值）对矩阵进行算术运算。这也是基于广播的功能

print(A)
print(A * 10)

数学上将一维数组称为‘向量’，将二维数组称为‘矩阵’，将一般化后的向量或矩阵等统称为‘张量’（tensor）。本书将二维数组称为矩阵，三维及以上称为‘张量’或‘多维数组’

1.5.5 广播

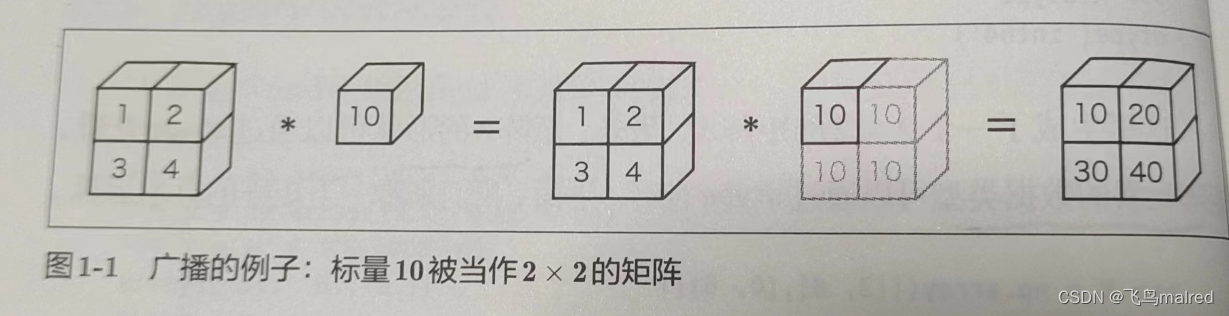
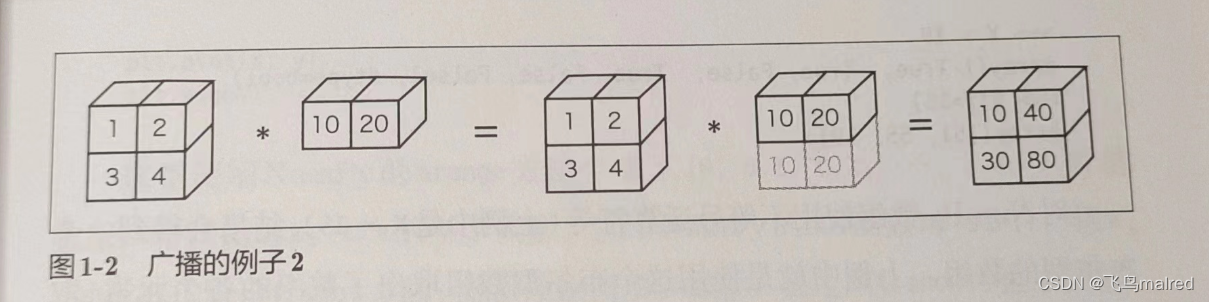
numpy 中形状不同的数组之间也可以进行运算。之前的例子中，2x2 的矩阵和标量 10 之间进行了乘法运算。这个过程中，标量 10 被扩展成
2x2 的形状，然后再与矩阵 A 进行乘法运算。这个功能就是广播

1.5.6 访问元素

X = np.array([[51, 55], [14, 19], [0, 4]])
print(X)
print(X[0])  # 第0行
print(X[0][1])  # (0,1)的元素

使用 for 遍历

for row in X:
print(row)

使用数组访问

X = X.flatten()  # 将X转为一维数组
print(X)
print(X[np.array([0, 2, 4])]) # 获取索引为0、2、4的元素

通过这个标记法，可以获取满足一定条件的元素。例如，获取 x 中大于 15 的元素

print(X > 15)
print(X[X > 15])

通过不等号得到了布尔型数组，并通过布尔型数组取出 X 的各个元素（取出 True 对应的元素）

• python 等动态语言一般比 c 和 c++等静态语言（编译型）运算速度慢，所以很多追求性能的场景，人们用 c、c++编写，然后让 python
  调用，numpy 也是如此

1.6 Matplotlib

图形绘制和可视化的库

1.6.1 绘制简单图形

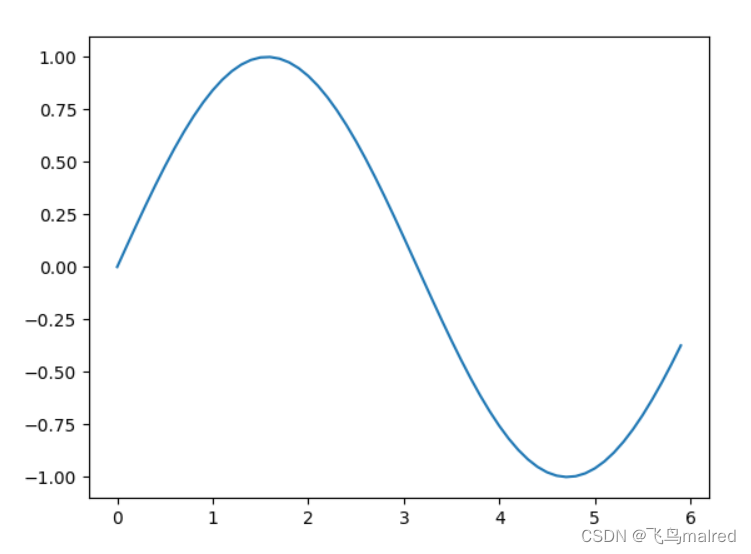
sin 函数曲线

import numpy as np
import matplotlib.pyplot as plt

# 生成数据
x = np.arange(0, 6, 0.1)  # 以0.1为步长（单位），生成0到6的数据
y = np.sin(x)

# 绘制图形
plt.plot(x, y)
plt.show()

1.6.2 pyplot 的功能

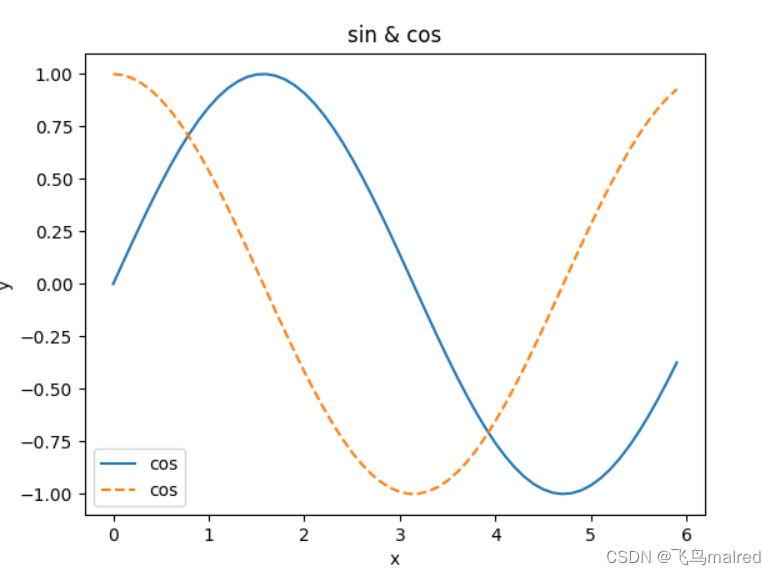
在刚才的 sin 函数图形中追加 cos 函数的图形，并尝试使用 pyplot 的添加标题和 x 轴标签名等其他功能

import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend('TkAgg')
# 绘制sin函数曲线
# 生成数据
x = np.arange(0, 6, 0.1)  # 以0.1为步长（单位），生成0到6的数据
y1 = np.sin(x)
y2 = np.cos(x)

# 绘制图形
plt.plot(x, y1, label='cos')
plt.plot(x, y2, linestyle='--', label='cos')  # 用虚线绘制 
plt.xlabel('x')  # x轴标签
plt.ylabel('y')  # y轴标签
plt.title('sin & cos')  # 标题
plt.legend()
plt.show()

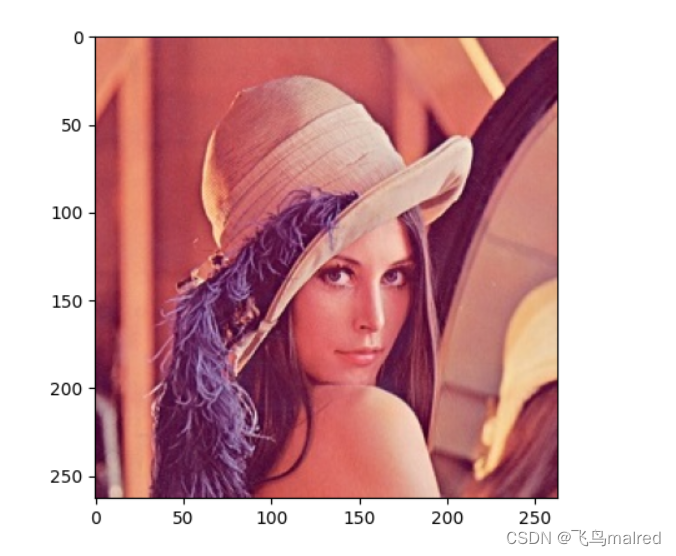
1.6.3 显示图像

pyplot 提供了显示图形的方法 imshow()。此外，还可以使用 matplotlib.image 里的 imread() 读取图像

import matplotlib.pyplot as plt
from matplotlib.image import imread

img = imread('lena.jpg')  # 读入图像（设定合适的路径）
plt.imshow(img)

plt.show()