CGAL中三角形曲面网格近似

1、介绍

????????此软件包实现了变分形状近似（VSA）方法，通过更简单的表面三角形网格来近似输入表面网格。该算法的输入必须是：

????????三角形分割；组合2流形

????????输出是一个三角形汤，可以构建成多边形曲面网格。

????????给定一个输入曲面三角网格，VSA利用离散聚类算法通过一组称为代理的局部简单形状对其进行近似。每个簇表示为输入网格的一组连接的三角形，输出网格是通过生成一个近似簇的曲面三角网格来构造的。近似误差是单边的，在簇与其相关代理之间定义。两个误差度量（L2和L1）用于评估簇的近似误差。

? ? ? ? 两个错误度量(?L22,?L2,1)?用于平面代理的算法是通过类CGAL::Surface_mesh_approximation::L2_metric_plane_proxy和CGAL::Surface_mesh_approximation::L21_metric_plane_proxy提供的，该算法设计对于其他用户定义的度量是通用的。当前的代理是平面或向量，但是该算法设计对于未来非平面代理的扩展是通用的。

????????默认的L2,1在计算和视觉感知方面，建议使用度量。

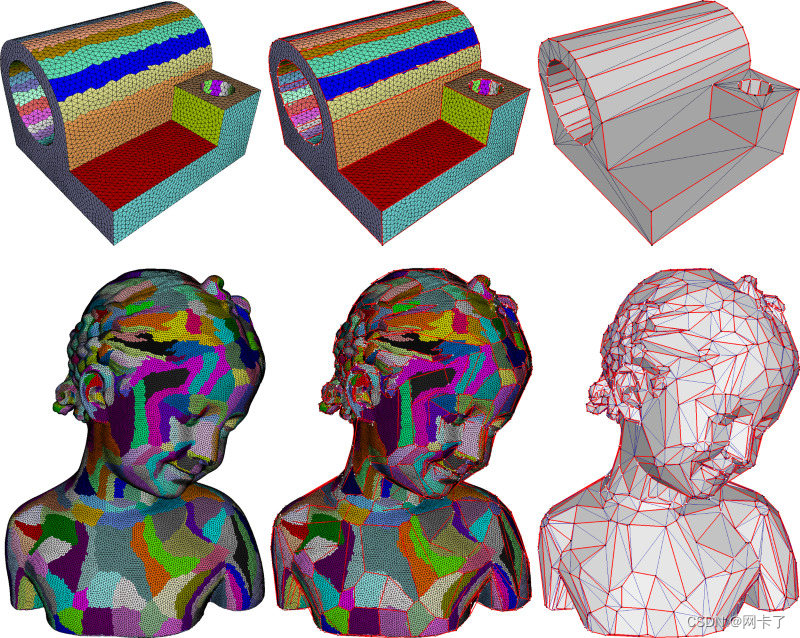
????????两个L2,1模型的变分形状近似;误差度量和平面代理。从左到右：输入曲面三角形网格、锚点顶点和边以及输出三角形网格的分区。通过输入三角形的离散聚类来优化分区，从而最小化从聚类到平面代理（未示出）的近似误差。

????????该软件包通过免费函数CGAL::Surface_mesh_approximation::approxy_triangle_mesh（）提供近似和网格构建功能，该函数运行该算法的全自动版本：?

????????还为高级用户提供了一个类接口，其中一系列顺从的操作符在集群和自定义过程中提供了交互功能，包括错误和代理。

2、整体

????????该软件包包含3个主要组件：近似算法、柔顺算子和网格划分，如图所示。

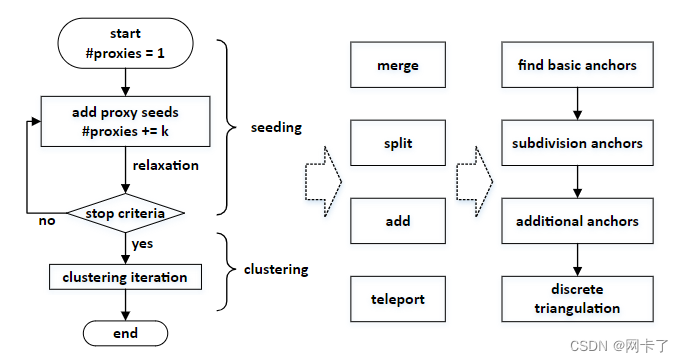
????????从左到右是近似包的三个组成部分：近似算法（左）、可选的服从运算（中）和网格划分（右）。?

2.1、近似

? ? ? ? 上图的左侧部分描述了近似算法的工作流程。

聚类迭代

? ? ? ? 下图描述了具有平面代理和L2,1的平面球体模型上的几个Lloyd聚类迭代。我们绘制了每次迭代的拟合误差。经过8次迭代后，误差几乎没有变化。基于这一观察结果，我们认为，如果当前迭代和先前迭代之间的误差变化低于用户指定的阈值（由两条绿色虚线表示），则聚类收敛。

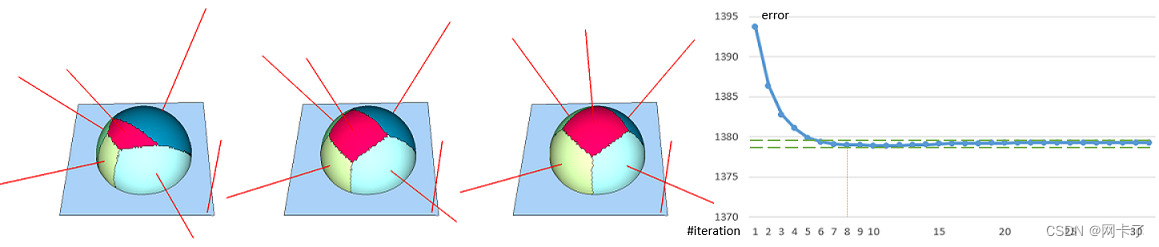
????????具有平面代理和L2,1的平面球体模型的离散Lloyd迭代度量：（左）6个代理的随机种子；（中心）一次迭代后；（右）经过8次迭代后，区域稳定下来。红线表示在种子面绘制的代理法线。?

种子

????????每个代理始终与输入曲面网格中的种子三角形面相关联。虽然从几何误差的角度来看，代理可以被视为中心（或最佳代表），但每个代理的种子被用作聚类过程中的起点。种子处理是指决定如何选择种子面的过程，新代理/分区可以从种子面初始化。

????????为了开始聚类迭代，我们需要一组初始代理。默认（分层）方法为每个连接的组件生成一个代理，以任意选择的面为种子。然后，它分批添加更多代理，以降低误差。在添加每一批代理后，它会执行几次内部聚类迭代，这在种子步骤中被称为松弛。

????????假设一个 n 维的聚类分区有误差的区域{Ek}k=1?n，我们希望添加m代理。我们提供3种不同的种子方法：

????????随机：种子面是在曲面上随机选取的，不包括当前的种子面。

????????增量式。每个新代理都从具有最大近似误差的区域的一个面初始化。该面本身被选为在其区域内实现最大误差的面。

????????等级制的面；种子面在当前的分区内被调度，其中每个区域都根据其拟合误差选择了一些代理进行细化：

????????计算总误差Etotal，则平均误差Eavg=Etotal/m（假设每个新代理共享相同的误差量）

????????排序错误 {Emin,?,Emax}
????????来自Emin到Emax，我们逐层扩散误差。更具体地说，代理的数量Nk添加到 kth 区域与其误差成正比

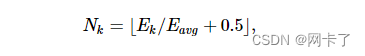
????????并且将剩余的错误添加到下一个代理错误，以保持总错误不变：?

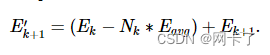
? ? ? ? 下图描述了不同的播种方法。

????????随机初始化随机选择一组输入三角形面作为代理种子。虽然它非常快，但随后的聚类过程可能会陷入糟糕的局部最小值，尤其是在区域被尖锐折痕包围的形状上（左特写）。

????????增量初始化在失真程度最高的区域逐个添加代理。因此，由于大量的交错弛豫迭代，它可能是缓慢的。

????????分层初始化（默认选择）在分层细化序列中重复加倍代理的数量，以生成拟合误差均匀分布的聚类区域。时间消耗通常介于前两者之间。统计和比较可参见性能一节。

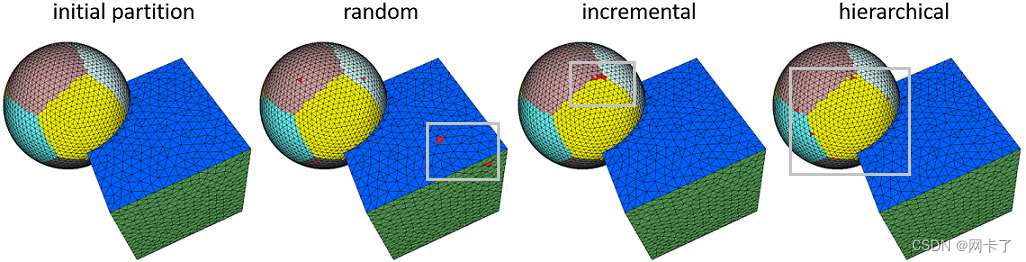
????????球体立方体模型上的不同播种方法。从左到右：初始分区（L2,1度量和20个代理），分别使用随机、增量和分层方法添加5个代理种子（红色面）。?

停止标准

????????为了确定何时停止添加更多代理，我们可以指定近似几何形状所需的最大代理数量，或者相对于第一个分区的最小误差下降百分比。更具体地说，我们可以决定：

????????代理的最大数量。添加代理，直到达到指定的数量。

????????最小误差下降。从第一个分区开始（每个连接的组件有一个代理），拟合误差为E^算法添加代理，直到近似误差降到指定的百分比 target_drop*E^。

????????如图所示，指定10%的最小误差下降（黄色虚线）作为停止标准，在平面-球面模型上产生了12个代理。当同时提供两个标准时，满足第一个标准即可停止播种。图描述了不同的播种示例。为了在性能和速度之间取得平衡，我们建议使用分层播种并指定两个停止标准。

????????使用不同数量的代理来近似平面球体模型。从左到右：8、14、20个代理。我们根据代理的数量来校正错误。?

2.2、柔顺操作

????????对于交互式使用，该方法可以通过添加/删除操作来更好地近似几何形状，并通过额外的操作从局部最小值中隧穿出来：

????????Merging。合并两个相邻的区域。

????????Splitting。将一个指定区域分割成更小的区域以减少误差。默认情况下执行二分法，但也可以执行N段法。我们首先从指定区域中选择请求数量的面部种子，然后在该区域内执行重新拟合过程。

????????Adding。添加一个或多个代理以进一步减少近似误差。对于种子过程，可以递增或分层添加，如图4所示。

????????Teleporting。传送操作符是合并和添加代理的组合：合并相邻区域对，并向最差区域添加代理种子。更具体地说，选择合并后实现最小误差的区域对进行合并和局部重新拟合。

????????在实践中，传送操作可以暂时降低或增加总近似误差。我们提供了一个可选的启发式方法来评估传送是否值得，通过验证（模拟）删除引起的误差增加是否小于最差区域误差的一半。如果该测试失败，则认为没有必要进行传送。

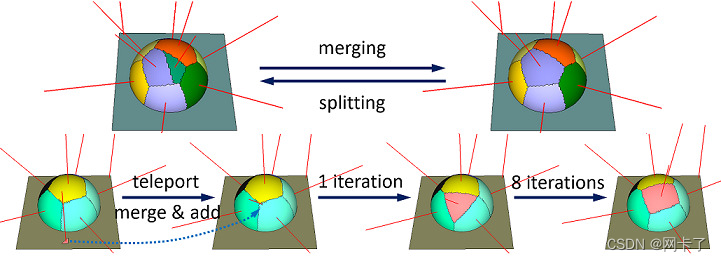
????????对球体-立方体并集模型的操作。上排：在受限区域上合并（9个代理）和反向平分拆分（10个分区）。下一行：一个隐形传送操作，合并并添加一个面种子，用一个代理来近似球体。?

????????如图所示，远距传物提供了一种方法，可以将平面部分（左）中包含的局部最小区域重新定位到球体（右）上最需要的区域。在类接口中，类接口用于通过上述操作控制近似过程。?

2.3、网格划分

????????该包通过生成聚类分区的三角形网格近似来实现[中描述的网格划分算法。网格划分算法有两个主要步骤：

????????寻找锚。锚点只是区域边界上输入网格顶点的子集。

????????离散约束二维Delaunay三角剖分。连接锚点以生成最终近似的三角形网格。

?基本锚点

????????如果顶点是锚：不是网格边界顶点并且与至少三个区域相邻，或者与至少两个区域相邻的网格边界顶点。

细分锚点

????????沿着代理区域的边界（逆时针方向）行走，弦是一系列连接两个锚点的半边。一个簇边界循环可能由几个弦组成。一个有孔的连接区域可能会产生几个边界循环（图6，传送前的平面部分）。

????????为了更好地近似复杂的边界，通过递归弦细分生成了更多的锚点（7）。锚点c
在弦（a，b）的最远顶点处添加，将其拆分为（a，c）和（c，b）；如果距离d=∥c,(a,b)∥
超过一定阈值。为了使d与输入规模无关

????????d=d/input_mesh_average_edge_length.

????????可选地，d可以测量为弦长的比率：

????????d=d/∥(a,b)∥.

????????此外，我们可以添加二面角权重sin(Ni,Nj)对于距离测量，其中Ni，Nj是由弦（a，b）分隔的代理的法线；如果代理Pi和代理Pj之间的角度更小，那么粗略的近似就可以了，因为它不会添加关于形状的几何信息。

????????如果弦不是圆形的，则不会对平凡的弦（少于4条边）进行细分。如果是圆形的弦，则可能会添加额外的锚点来保持拓扑结构，即使它们是平凡的，如“附加锚点”一节中详细描述的那样。

????????改变弦误差。从左到右：聚类划分，并在没有二面角权重的情况下以减小绝对弦误差5、3和1进行网格划分。分区的边界（红线）以越来越高的精度进行近似。?

增加锚点

????????对于没有任何锚的边界循环，如图6所示的孔，我们首先在边界上添加一个起始锚。然后，我们对这个圆形弦进行细分，以确保每个边界循环至少有2个锚（即，每个弦连接2个不同的锚，图8）。最后，我们添加额外的锚，以确保在每个边界循环上至少生成三个锚顶点。

????????添加锚点。从左到右：从一个带孔（while）和两个环绕区域（绿色和蓝色）的分区（灰色）开始，我们在没有任何锚点的边界循环（红色虚线）中添加一个起始锚点（橙色圆盘）（第2个），细分圆弦（第3个，数字表示递归级别），并在少于2个锚点的边界周期中添加锚点（第4个，红色虚线）。?

离散三角剖分

????????锚点定义后，它们的弦连接图形成了一个普通的多边形网格。由于非平面、凹多边形或有孔的多边形，我们需要对初始的多边形网格进行三角剖分。三角剖分是通过计算受约束的二维Delaunay三角剖分的离散变体而生成的，其中距离是在输入的三角形网格上测量的。

????????图的第一幅图描述了如何通过连接3个Voronoi单元相遇的顶点（红色圆圈）所指示的点，从其对偶Voronoi图（由蓝线分隔的彩色区域）中推导出点集（彩色圆盘）的Delaunay三角剖分。以类似的方式，我们构造了离散的Voronoi单元，从中提取三角剖分。

????????在第一步中，我们开始对该区域的内部进行泛色，根据其最近的锚点对顶点进行着色。然后，我们只对区域的边界进行泛色，以便其上的每个顶点都根据最近的锚点进行着色。这通过强制边界位于其中来强制约束边缘。

球体模型上的离散约束三角剖分。三角剖分过程首先淹没内部顶点（红色箭头，第二个）以模拟Voronoi图。然后，它通过沿边界边进行泛洪处理（红色箭头，第三个），在锚点顶点之间构造受约束的边。最后，通过连接3个Voronoi单元相交的面（红色实心三角形，第4个）的源锚（黑色箭头，第4），形成三角形（红色空心三角形，第四个）。?

????????在每个聚类区域进行三角剖分后，通过计算锚点在其相邻代理上的投影的平均值，重新计算最终的锚点位置。

????????在下图中，通过L2,1度量来近似熊模型，最终的代理数量是通过监控误差下降来确定的。锚点（黑色）附着在网格上的相应顶点（白色）上。连接锚点的红色线近似每个区域的边界。

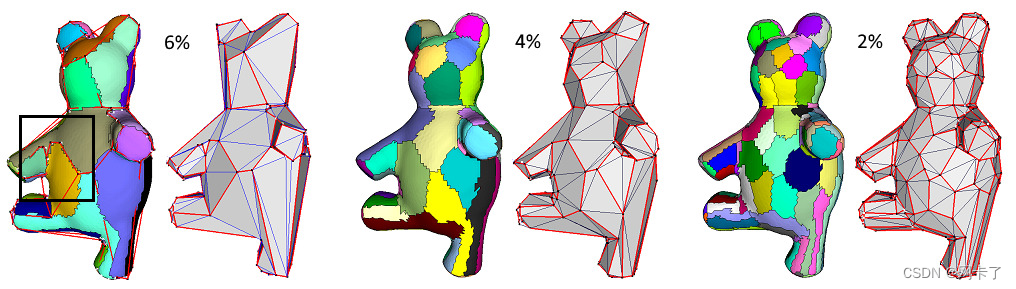
对目标误差下降较小的熊模型进行网格划分。从左到右，目标误差分别比初始误差下降6%、4%和2%，输出网格致密化。请注意黑色矩形区域中的边界细分。

????????由于无法保证输出网格是2-流形和定向的，因此主输入是一个索引三角形集。我们可以使用多边形汤将三角形汤构建为有效的多边形网格。

2.4、API

????????这个包可以与CGAL和Boost图库中描述的FaceListGraph概念的任何类模型一起使用。

????????带有命名参数选项的自由函数。

????????CGAL::Surface_mesh_approximation::approxy_triangle_mesh（）：给定三角形网格，使用默认L2,1近似几何。

????????类接口：CGAL::Variational_shape_approximation：允许对代理、度量和近似过程进行更多自定义。如图2所示，近似和网格划分过程的典型调用顺序为：

????????初始化种子；运行集群迭代；提取网格；获取输出

????????需要注意的一点是，有些参数在很大程度上取决于输入，比如代理的数量。尽管无论质量如何，我们都可以使用任何数量的代理来近似几何体，但不建议在不考虑输入的情况下使用所有默认值。

3、性能

????????我们提供了一些与自由函数API CGAL::Surface_mesh_approximation::approxy_triangle_mesh的性能比较。计时记录在运行Windows10 X64的PC上，该PC配有Intel Xeon E5-1620，频率为3.70 GHz，内存为32GB。该程序已使用Visual Studio 2015的O2选项进行了优化。默认使用的内核是 Exact_predicates_inexact_constructions_kernel (EPICK)。

????????不同种子方法的目标代理数对应的运行时间（秒）

Model	#Triangles	#Proxies	Random	Incremental	Hierarchical
plane-sphere	6,826	20	0	0.87	0.17
bear	20,188	200	0	36.749	1.194
masque	62,467	200	0.002	133.901	4.308

?????????不同种子设定方法的目标错误下降的运行时间（秒）。该基准是在拥有20188张面孔的熊模型上运行的。每一列都记录时间和代理的结果数量：

Target Error Drop	Random	Incremental	Hierarchical
0.06	1.03/64	9.053/53	1.017/64
0.04	1.207/128	15.422/88	1.2/128
0.02	1.415/256	35.171/192	1.428/256

?????????算法的三个阶段的运行时间（秒）：种子、聚类迭代和网格划分。种子方法是分层的，具有目标数量的代理。

Model	#Triangles	#Proxies	#Iterations	Seeding	Clustering	Meshing	Total
plane-sphere	6,826	20	20	0.17	0.228	0.044	0.442
bear	20,188	200	20	1.194	0.784	0.128	2.006
masque	62,467	200	20	4.308	2.974	0.349	7.631

4、背景

????????VSA方法有两个关键的几何概念：

????????代理服务器 P，曲面几何形状的参数化最佳拟合替代。

????????误差度量 E，?测量代理与相应几何体的近似程度。

????????给定误差度量E，期望数量 k代理和输入表面S，我们用最优形状代理表示代理Pi的集合P与区域Ri相关联R的分割S的使总装配误差最小化。?

?

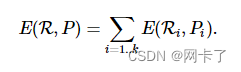
????????通过将近似问题转化为最优的离散聚类问题，该算法利用有效的Lloyd算法迭代地降低总误差。更具体地说，在每次迭代中，对m次迭代：

????????分割过程。首先，将所有三角形面分割成k连接区域{Rm1,?,Rmk}；通过将每个面部分配给其最近的代理Pm?1i。

????????拟合过程。然后，算法拟合一个代理并更新参数Pmi；从相应区域Rmi。

????????对于拟合误差为{E1,?,Em}的迭代序列，重复迭代直到满足其中一个停止标准：?

????????达到最大迭代次数：m>=max_iterations。

????????两次迭代之间没有明显的误差变化：（Em?1?Em）/Em?1<收敛阈值。

????????.直观地，每个区域Ri分区R的可以概括地表示为一阶“平均”点Xi和“平均”正常Ni我们表示这样的局部代表对Pi=（Xi，Ni），相关区域的平面代理。

????????定义一个适当的误差度量是该算法的关键要素。L2度量被定义为

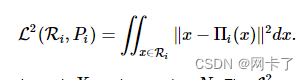
????????其中 Πi(?)表示将参数投影到通过 Xi且与 Ni垂直的代理平面上。L2指标试图通过几何位置的近似来匹配输入形状。

????????在原始论文中，作者提出了 L2,1指标，并认为法线对于形状的视觉解释非常重要。L2,1
定义为：?

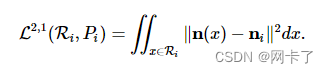
????????L2,1在数值上优于L2从几个方面来看：

????????更好地捕捉了表面的各向异性。

????????找到最好的法线代理就像求法线平均值一样简单。

5、其他

????????聚类是一种数据分析和处理技术，其目标是将数据集划分为多个相似的组或“簇”。每个簇中的数据点彼此相似，但与其他簇中的数据点不同。

????????聚类的过程大致如下：

????????选择聚类算法：有很多不同的聚类算法，如K-means、层次聚类、DBSCAN等。选择合适的算法对于结果至关重要。

????????确定簇的数量：在某些算法（如K-means）中，需要预先指定簇的数量。在其他算法中，可能可以自动确定簇的数量。

????????计算距离：计算数据点之间的距离是聚类的关键步骤。常见的距离度量有欧几里得距离、曼哈顿距离等。

????????将数据点分配到簇：根据距离度量和其他因素（如密度或连通性），将数据点分配给各个簇。

????????评估和优化：评估聚类结果，根据需要进行调整，例如更改聚类算法、调整参数等。

????????Lloyd算法，也被称为Lloyd迭代算法或K-means算法，是一种用于数据聚类的迭代优化算法。其核心思想是通过迭代的方式将数据点分配到不同的簇中，使得每个簇内部的数据点尽可能相似，而不同簇之间的数据点尽可能不相似。

????????Lloyd算法的步骤如下：初始化：随机选择K个聚类中心，可以随机选择K个数据点作为初始聚类中心。簇分配：将所有的数据点分配到最近的聚类中心，这一步也被称为“簇分配”。中心更新：根据已经分配到每个聚类中心的数据点，更新聚类中心的位置，使得每个聚类中心都处于其所包含数据点的中心位置，这一步被称为“中心更新”。重复进行簇分配和中心更新的步骤，直到聚类中心不再发生变化或者达到预设的迭代次数。

????????这个算法的主要优点是简单且易于实现，因此在许多领域得到了广泛应用。然而，它也有一些局限性，例如对初始聚类中心的选择敏感，可能会陷入局部最优解等。