【数据结构】二叉搜索树

---

一、二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树：

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树

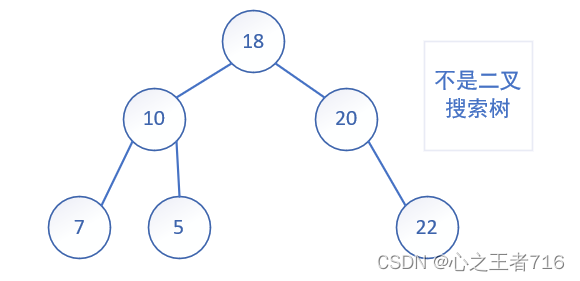
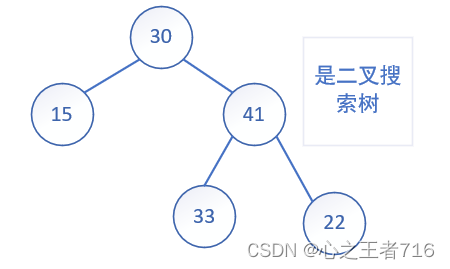
二、二叉搜索树操作

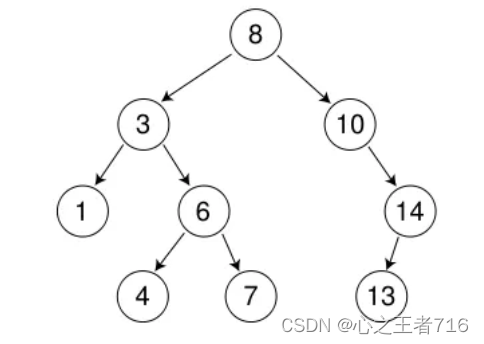
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};

1. 定义二叉树节点

template<class K>
struct BSTreeNode
{
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

2. 二叉树的插入

两种情况：

1. 树为空，则直接新增节点，赋值给root指针
2. 树不空，按二叉搜索树性质查找插入位置，插入新节点

// 非递归版本
bool Insert(const K& key)
{
	// 1.树为空，直接新增结点
	if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
	// 2.树不空，按二叉搜索树性质查找插入位置，插入新节点
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		parent = cur;

		if (cur->_key < key)
		{
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	cur = new Node(key);
	if (parent->_key < key)
	{
		parent->_right = cur;
	}
	else
	{
		parent->_left = cur;
	}

	return true;
}

// 因为类外面拿不到根节点，但类里面可以，所以在类里面定义一个函数
// 通过类里面去调用
bool InsertR(const K& key)
{
	return _InsertR(_root, key);
}

// 递归版本
bool _InsertR(Node*& root, const K& key)
{
	if (root == nullptr)
	{
		root = new Node(key);
		return true;
	}

	if (root->_key < key)
	{
		return _InsertR(root->_right, key);
	}
	else if (root->_key > key)
	{
		return _InsertR(root->_left, key);
	}
	else
	{
		return false;
	}

}

3. 二叉树的查找

1. 从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
2. 最多查找高度次，走到到空，还没找到，这个值不存在。

// 非递归版本
bool Find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
		{
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			cur = cur->_left;
		}
		else
		{
			return true;
		}
	}

	return false;
}

// 递归版本
bool FindR(const K& key)
{
	return _FindR(_root, key);
}

bool _FindR(Node* root, const K& key)
{
	if (root == nullptr)
	{
		return false;
	}
	
	if (root->_key < key)
	{
		return _FindR(root->_right, key);
	}
	else if (root->_key > key)
	{
		return _FindR(root->_left, key);
	}
	else
	{
		return true;
	}
}

4. 二叉树的删除

二叉树的删除情况比较复杂，首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情况：

1. 要删除的结点无孩子结点
2. 要删除的结点只有左孩子结点
3. 要删除的结点只有右孩子结点
4. 要删除的结点有左、右孩子结点

但是第一种情况可以和第二种或者第三种情况合并，所以删除过程有下面三种：

• 情况2：删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
• 情况3：删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
• 情况4：将该节点与左子树的最大节点或者右子树的最小节点交换，然后再删除该节点–替换法删除

// 非递归版本
bool Erase(const K& key)
{
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		// 先循环找到要删除的节点
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			// 左孩子为空
			if (cur->_left == nullptr)
			{
				// 如果删除根节点，则直接将右孩子赋给根节点
				if (cur == _root)
				{
					_root = cur->_right;
				}
				else
				{
					// 如果待删除节点是左孩子
					// 则让待删除节点的右孩子赋给待删除节点的父节点的左孩子
					if (cur == parent->_left)
					{
						parent->_left = cur->_right;
					}
					// 同理
					else
					{
						parent->_right = cur->_right;

					}
				}
				delete cur;
			}
			// 右孩子为空
			else if (cur->_right == nullptr)
			{
				// 如果删除根节点，则直接将左孩子赋给根节点
				if (cur == _root)
				{
					_root = cur->_left;
				}
				// 如果待删除节点是左孩子
				// 则让待删除节点的左孩子赋给待删除节点的父节点的左孩子
				else
				{
					if (cur == parent->_left)
					{
						parent->_left = cur->_left;
					}
					else
					{
						parent->_right = cur->_left;

					}
				}
				delete cur;
			}
			// 左右都不为空
			else
			{
				// 右子树的最小节点(最左节点)
				Node* parent = cur;
				Node* subLeft = cur->_right;
				while (subLeft->_left)
				{
					parent = subLeft;
					subLeft = subLeft->_left;
				}
				// 交换值
				swap(cur->_key, subLeft->_key);
				if (subLeft == parent->_left)
				{
					parent->_left = subLeft->_right;
				}
				else
				{
					parent->_right = subLeft->_right;
				}
				delete subLeft;
			}
			return true;
		}
	}
	return false;
}

// 递归版本
bool EraseR(const K& key)
{
	return _EraseR(_root, key);
}

bool _EraseR(Node*& root, const K& key)
{
	if (root == nullptr)
		return false;
	if (root->_key < key)
	{
		return _EraseR(root->_right, key);
	}
	else if (root->_key > key)
	{
		return _EraseR(root->_left, key);
	}
	else
	{
		if (root->_left == nullptr)
		{
			Node* del = root;
			root = root->_right;
			delete del;

			return true;
		}
		else if (root->_right == nullptr)
		{
			Node* del = root;
			root = root->_left;
			delete del;

			return true;
		}
		else
		{
			// 右树的最小节点(最左节点)
			Node* subLeft = root->_right;
			while (subLeft->_left)
			{
				subLeft = subLeft->_left;
			}

			swap(root->_key, subLeft->_key);

			// 转换成在子树去递归删除
			return _EraseR(root->_right, key);
		}
	}
}

---