二叉搜索树(Binary Search Tree)

二叉搜索树(Binary Search Tree)

二叉搜索树是一种特殊的二叉树，它的每个节点的键都大于其左子树中的任意节点的键，而小于右子树的任意节点的键。

下面是一个二叉搜索树的示例：

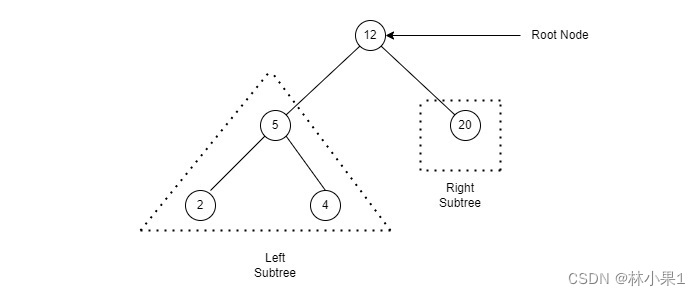
二叉搜索树初始化

创建树节点的静态内部类，初始化根节点root

BSTreeNode root;

static class BSTreeNode {
    int key;
    Object value;
    BSTreeNode left;
    BSTreeNode right;

    public BSTreeNode(int key) {
        this.key = key;
    }

    public BSTreeNode(int key, Object value) {
        this.key = key;
        this.value = value;
    }

    public BSTreeNode(int key, Object value, BSTreeNode left, BSTreeNode right) {
        this.key = key;
        this.value = value;
        this.left = left;
        this.right = right;
    }
}

二叉搜索树的操作

二叉搜索树支持多种操作，包括插入、查找、删除等。以下是这些操作的Java实现。

插入操作（put）

插入操作是将一个新的键值对插入到二叉搜索树中。如果树中已经存在相同的键，那么新的值将替换旧的值。

public boolean put(int key, Object value) {
    BSTreeNode node = root;
    BSTreeNode parent = null;
    // 通过循环找到要插入的位置
    while (node != null) {
        parent = node;
        if (key > node.key)
            node = node.right;
        else if (key < node.key)
            node = node.left;
        else {
            // 如果找到了相同的键，就更新值
            node.value = value;
            return true;
        }
    }
    // 创建新的节点
    BSTreeNode bsTreeNode = new BSTreeNode(key, value);
    // 如果树为空，就让新节点成为根节点
    if (parent == null) {
        root = bsTreeNode;
    } else if (key > parent.key) {
        parent.right = bsTreeNode;
    } else {
        parent.left = bsTreeNode;
    }
    return true;
}

查找操作（get）

查找操作是根据键在二叉搜索树中查找对应的值。

public Object get(int key) {
    return doGet(root, key);
}

private Object doGet(BSTreeNode node, int key) {
    // 如果节点为空，返回null
    if (node == null)
        return null;
    if (node.key > key)
        return doGet(node.left, key);
    else if (node.key < key)
        return doGet(node.right, key);
    else
        // 如果找到了键，就返回对应的值
        return node.value;
}

删除操作（delete）

删除操作是从二叉搜索树中删除一个键值对。如果树中不存在该键，那么操作无效。

这里我们提供两种实现方式，一种是使用循环，另一种是使用递归。

使用循环实现删除操作

public Object delete(int key) {
    BSTreeNode node = root;  // 从根节点开始
    BSTreeNode parent = null;  // 记录父节点
    while (node != null) {  // 遍历树，直到找到节点或到达叶子节点
        if (node.key > key) {  // 如果当前节点的键大于要查找的键，向左遍历
            parent = node;
            node = node.left;
        } else if (node.key < key) {  // 如果当前节点的键小于要查找的键，向右遍历
            parent = node;
            node = node.right;
        } else {  // 如果键匹配，跳出循环
            break;
        }
    }
    // 如果节点未找到，返回null
    if (node == null)
        return null;
    // 如果节点没有左子树，那么用右子树替换该节点
    if (node.left == null) {
        shift(parent, node, node.right);
    // 如果节点没有右子树，那么用左子树替换该节点
    } else if (node.right == null) {
        shift(parent, node, node.left);
    // 如果节点既有左子树又有右子树
    } else {
        BSTreeNode p = node.right;
        BSTreeNode pParent = node;
        // 找到右子树中的最小节点
        while (p.left != null) {
            pParent = p;
            p = p.left;
        }
        // 如果最小节点不是直接的右子节点，需要做一些调整
        if (p != node.right) {
            pParent.right = p.right;
            p.right = node.right;
        }
        p.left = node.left;
        shift(parent, node, p);
    }
    return node.value;
}

private void shift(BSTreeNode parent, BSTreeNode p, BSTreeNode child) {
    if (parent == null) {
        root = child;
    } else if (parent.left == p) {
        parent.left = child;
    } else if (parent.right == p) {
        parent.right = child;
    }
}

使用递归实现删除操作

public Object delete(int key) {
    BSTreeNode node = doDelete(root, key);
    return node != null ? node.value : null;
}

private BSTreeNode doDelete(BSTreeNode node, int key) {
    if (node.key > key) {
        node.left = doDelete(node.left, key);
        return node;
    } else if (node.key < key) {
        node.right = doDelete(node.right, key);
        return node;
    } else {
        if (node.right == null) {
            return node.left;
        } else if (node.left == null) {
            return node.right;
        } else {
            BSTreeNode p = node.right;
            while (p.left != null) {
                p = p.left;
            }
            p.right = doDelete(node.right, p.key);
            p.left = node.left;
            return p;
        }
    }
}

查找所有小于给定值的节点（less）

这个操作是查找二叉搜索树中所有小于给定值的节点。

public List<Object> less(int key){
    ArrayList<Object> result = new ArrayList<>(); // 创建结果列表
    Stack<BSTreeNode> stack = new Stack<>(); // 创建一个栈来存储节点
    BSTreeNode p = root; // 从根节点开始
    while(p != null || !stack.isEmpty()){ // 遍历树
        if(p != null){
            stack.add(p); // 将节点加入栈中
            p = p.left; // 遍历左子树
        }else {
            BSTreeNode pop = stack.pop(); // 当左子树遍历完后，处理栈中的节点
            if(pop.key < key) // 如果节点的键值小于给定值，将其加入结果列表
                result.add(pop.key);
            else
                break; // 如果节点的键值大于或等于给定值，结束遍历
            p = pop.right; // 处理右子树
        }
    }
    return result; // 返回结果列表
}

查找所有大于给定值的节点（greater）

这个操作是查找二叉搜索树中所有大于给定值的节点。

public List<Object> greater(int key){
    ArrayList<Object> result = new ArrayList<>(); // 创建结果列表
    Stack<BSTreeNode> stack = new Stack<>(); // 创建一个栈来存储节点
    BSTreeNode p = root; // 从根节点开始
    while(p != null || !stack.isEmpty()){ // 遍历树
        if(p != null){
            stack.add(p); // 将节点加入栈中
            p = p.right; // 遍历右子树
        }else {
            BSTreeNode pop = stack.pop(); // 当右子树遍历完后，处理栈中的节点
            if(pop.key > key) // 如果节点的键值大于给定值，将其加入结果列表
                result.add(pop.key);
            else
                break; // 如果节点的键值小于或等于给定值，结束遍历
            p = pop.left; // 处理左子树
        }
    }
    return result; // 返回结果列表
}

查找所有在两个给定值之间的节点（between）

这个操作是查找二叉搜索树中所有在两个给定值之间的节点。

public List<Object> between(int key1,int key2){
    ArrayList<Object> result = new ArrayList<>(); // 创建结果列表
    Stack<BSTreeNode> stack = new Stack<>(); // 创建一个栈来存储节点
    BSTreeNode p = root; // 从根节点开始
    while(p != null || !stack.isEmpty()){ // 遍历树
        if(p != null){
            stack.add(p); // 将节点加入栈中
            p = p.left; // 遍历左子树
        }else {
            BSTreeNode pop = stack.pop(); // 当左子树遍历完后，处理栈中的节点
            if(key1 < pop.key && pop.key < key2) // 如果节点的键值在两个给定值之间，将其加入结果列表
                result.add(pop.key);
            else if(pop.key > key2)
                break; // 如果节点的键值大于给定值，结束遍历
            p = pop.right; // 处理右子树
        }
    }
    return result; // 返回结果列表
}