2024-01-03 无重叠区间
发布时间:2024年01月10日
435. 无重叠区间
思路:和最少数量引爆气球的箭的思路基本都是一致了!贪心就是比较左边的值是否大于下一个右边的值
class Solution:
def eraseOverlapIntervals(self, points: List[List[int]]) -> int:
points.sort(key=lambda x: (x[0], x[1]))
# 比较边界
res = points[0][1]
count = 0
for i in range(1, len(points)):
if points[i][0] < res:
res = min(res, points[i][1])
count += 1
else:
res = points[i][1]
return count
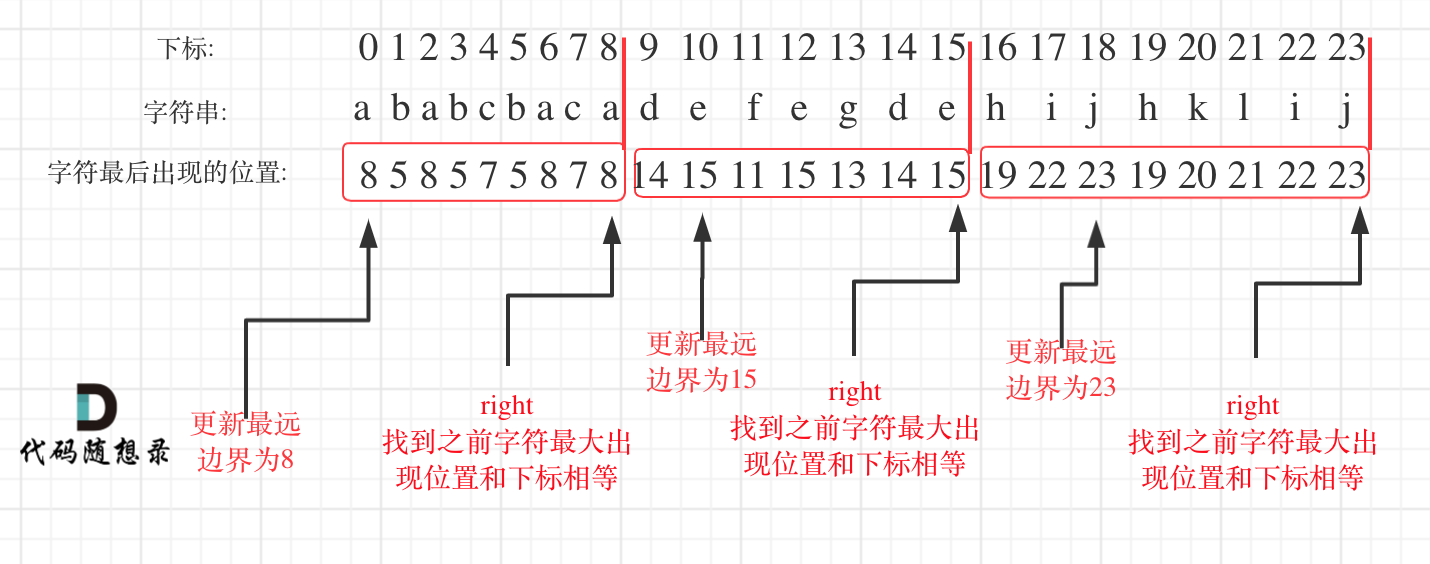
763. 划分字母区间
贪心思路:第一个字母最后出现的位置的过程中其他字母也出现的最后位置的最大值,就是一次划分区域了!

class Solution:
def partitionLabels(self, s: str) -> List[int]:
# 字母出现次数?
# 每一次字母最后出现的位置以及
mm = {}
for i in range(len(s)):
mm[s[i]] = i
start = 0
max_temp = mm[s[0]]
res = []
for i in range(len(s)):
if max_temp == i:
res.append(max_temp - start + 1)
start = i + 1
if i + 1 < len(s):
max_temp = mm[s[i + 1]]
elif mm[s[i]] > max_temp:
max_temp = mm[s[i]]
return res
class Solution:
def partitionLabels(self, s: str) -> List[int]:
last_occurrence = {} # 存储每个字符最后出现的位置
for i, ch in enumerate(s):
last_occurrence[ch] = i
result = []
start = 0
end = 0
for i, ch in enumerate(s):
end = max(end, last_occurrence[ch]) # 找到当前字符出现的最远位置
if i == end: # 如果当前位置是最远位置,表示可以分割出一个区间
result.append(end - start + 1)
start = i + 1
return result
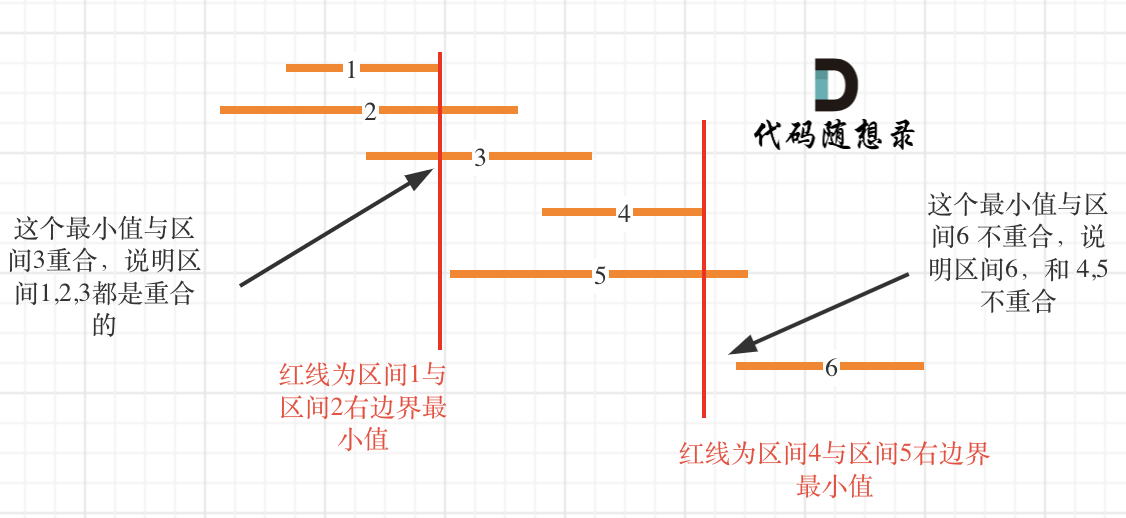
56. 合并区间
思路:就是如果区间的重叠的哇,就去重叠区间之间的最小值和最大值!关键还是拆分排序
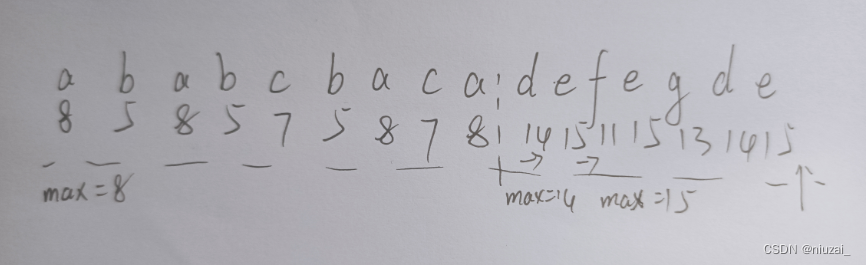
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
res = []
intervals.sort(key=lambda x :(x[0], x[1]))
index = 0
max_broad = intervals[0][1]
for i in range(1, len(intervals)):
if intervals[i][0] <= max_broad:
intervals[index][0] = min(intervals[index][0], intervals[i][0])
intervals[index][1] = max(intervals[index][1], intervals[i][1])
max_broad = intervals[index][1]
else:
res.append(intervals[index])
index = i
max_broad = intervals[i][1]
if intervals[index] not in res:
res.append(intervals[index])
return res
文章来源:https://blog.csdn.net/niuzai_/article/details/135514353
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 什么是web?web前端开发人员负责什么?
- CHS_01.2.2.1+调度的概念、层次
- Linux世界的奇妙之旅:开源之道的探索与分享
- 【Spring连载】使用Spring访问 Apache Kafka(六)----应用程序事件
- 运维工程师的出路到底在哪里?
- 文件包含漏洞概述、特征、利用条件、危害、防御
- 如何将请求参数及限制精确提示给用户,提示支持中英文切换
- 《volatile使用与学习总结:2023-12-17》多层面分析学习java关键字--volatile
- java编译运行测试
- 组播地址段及其作用