ReTree：扩散模型 + 视网膜图像生成

ReTree：扩散模型 + 视网膜图像生成

• • 核心思想
  • • 网络结构
    • 损失函数

?

---

核心思想

论文链接：https://arxiv.org/abs/2308.08339

代码链接：https://github.com/AAleka/retree

在视网膜图像合成方面表现优于传统的生成对抗网络（GAN）。

• EyeQ数据集中的真实视网膜图像（左侧）
• 生成的视网膜图像（右侧）

模型 分为两阶段。

• 第一阶段是生成血管树，它基于标准正态分布的随机数。
• 第二阶段是引导模型根据给定的血管树和随机分布来生成眼底图像。

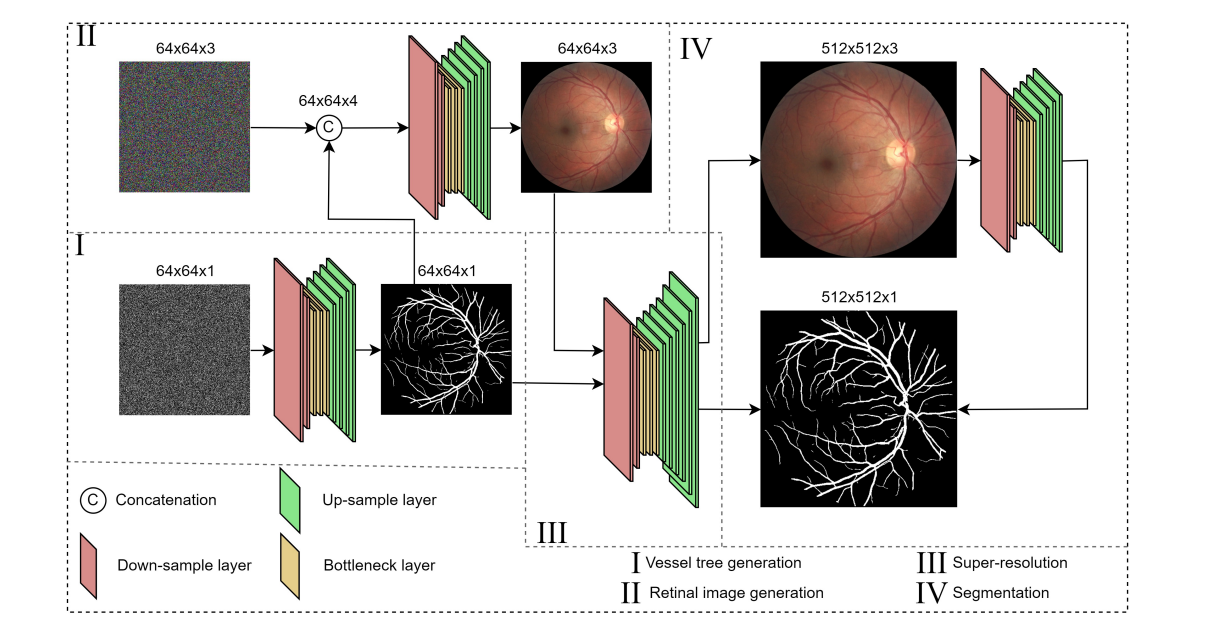
1. 血管树生成：首先，利用去噪扩散概率模型（DDPM）从噪声中生成血管树。
2. 视网膜图像生成：接着，另一个DDPM学习如何根据血管树和相应的语义标签图来生成视网膜图像。
3. 超分辨率：然后，对生成的血管树图像执行超分辨率处理，以增加图像的分辨率。
4. 分割：最后，利用生物医学分割模型对生成的并经过上采样的视网膜图像进行分割以进行验证。

网络结构

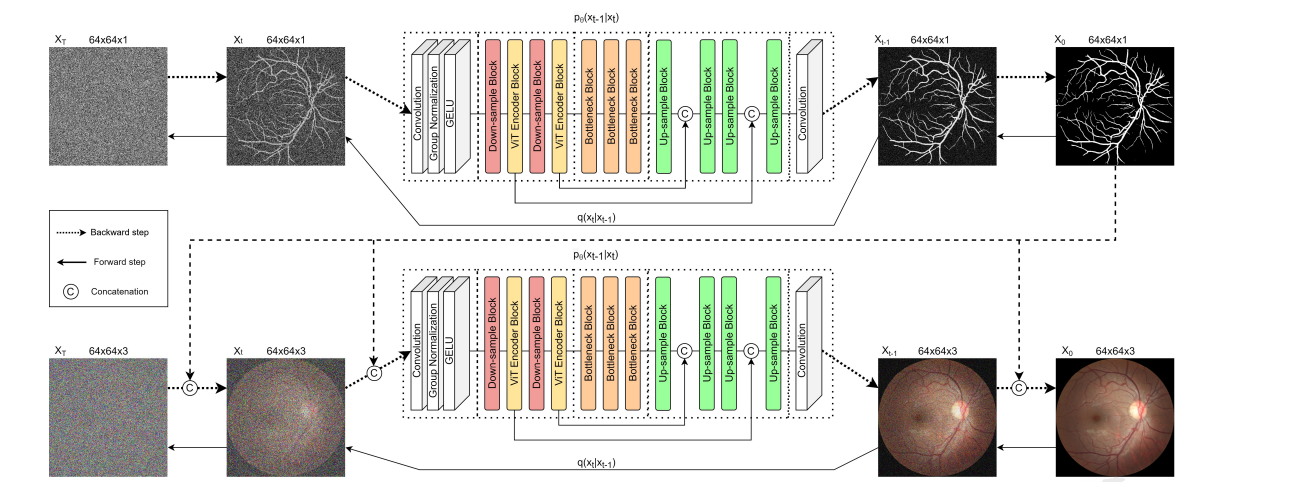
两个DDPM模型和ta们在生成视网膜图像过程中的作用：

1. 第一个模型（上半部分）：这个模型负责生成语义标签图。

• 它从包含噪声的图像XT开始，在给定的时间步长内通过添加高斯噪声模拟前向扩散过程（向左的箭头表示前向步骤），然后再通过DDPM去除噪声模拟后向过程（向右的箭头表示后向步骤），最终输出一个去噪后的血管树图X1。

2. 第二个模型（下半部分）：它采用第一个模型输出的血管树图X1和包含噪声的RGB图像XT，通过相同的前向扩散和后向去噪过程，生成最终的去噪后的彩色视网膜图X0。

每个模型都包含以下部分：

• 下采样层（Down-sample Block）：用于减少图像的空间维度，从而在更小的维度上捕获特征。
• ViT编码器（ViT Encoder Block）：利用Vision Transformer对特征进行编码。
• 瓶颈层（Bottleneck Block）：在模型的中心点处理特征，可能是为了进一步提炼它们。
• 上采样层（Up-sample Block）：将图像的空间维度增加回原始尺寸。

在每个扩散步骤t，模型都会预测给定扩散步骤t-1的输出。

每个DDPM模型的输出都用作下一步的输入。

在第一个模型中，血管树图像与带噪声的输入进行了连接（Concatenation），在第二个模型中，彩色视网膜图像与带噪声的输入进行了连接。

整个流程展示了一个完整的数据生成和处理流程：

• 从带有高斯噪声的图像开始，经过一系列的处理步骤，最终生成清晰的血管树图像和对应的彩色视网膜图像。

?

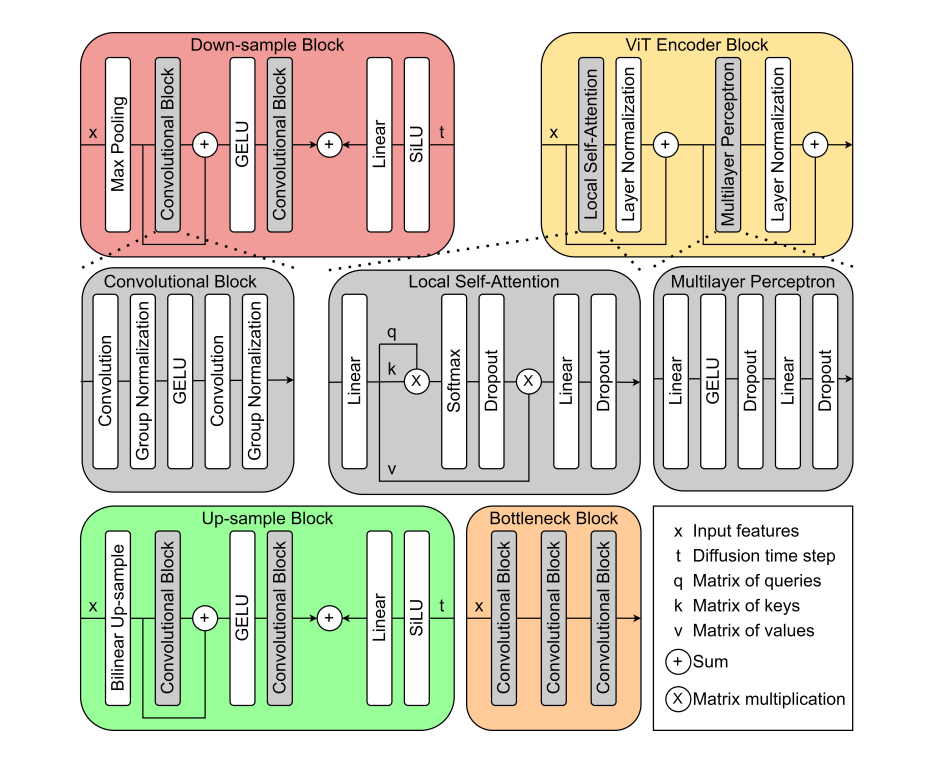
去噪扩散概率模型（DDPM）的架构，由四个主要部分组成：下采样块、ViT编码器块、上采样块和瓶颈块。

1. 下采样块（红色区域）：包括最大池化层（Max Pooling）、两个卷积层（Convolutional Block）、GELU激活函数、一个线性层（Linear），以及Sigmoid Linear Unit（SiLU）激活函数。

• 这个块的目的是减少输入特征的空间维度（即降低图像的分辨率），同时保留重要的特征信息。

2. ViT编码器块（黄色区域）：结合了局部自注意力机制（Local Self-Attention）、层归一化（Layer Normalization）和多层感知机（Multilayer Perceptron）。

• 这一部分的目的是捕捉输入特征之间的复杂关系，并增强模型对输入数据的理解。

3. 上采样块（绿色区域）：使用双线性上采样（Bilinear Up-sample）和两个卷积块，以及加法操作和SiLU激活函数。

• 这个块的作用是将降低分辨率后的特征图像恢复到更高的分辨率。

4. 瓶颈块（蓝色区域）：由三个连续的卷积块组成。

• 这个块位于模型的中心，用于进一步处理和提纯特征。

图中还展示了各个部分的输入和输出关系，以及其中使用的矩阵乘法（×）和加法（+）操作。

例如，在ViT编码器块中，q（查询矩阵）、k（键矩阵）和v（值矩阵）参与了矩阵乘法和Softmax操作以实现自注意力机制。

在整个模型中，t表示扩散时间步，它在模型的不同阶段被用来调整输入特征和生成的时间嵌入。

损失函数

1. DDPM的损失函数：DDPM使用了两种损失函数的组合，即L1损失（或称平均绝对误差MAE）和均方误差（MSE）。

   这两种损失函数用于计算预测噪声和实际应用噪声之间的差异

   $\text{GenLoss}({?}_{\theta }(x_t,t),z)=\frac{1}{N}{\sum }_{i=1}^N(|{?}_{\theta }?z|+({?}_{\theta }?z{)}^2)$

   N是图像像素的总数，${?}_{\theta }$ 是预测的噪声，z是实际应用的噪声。

2. 超分辨率模型的损失函数：超分辨率模型使用了五种损失函数的组合，包括L1损失、结构相似性指数（SSIM）、对抗损失、二元交叉熵（BCE）和感知损失。

   SSIM用于计算两幅图像之间的结构相似性：

   $\text{SSIM}(X,Y)=\frac{(2{\mu }_X{\mu }_Y+C1)(2{\sigma }_{XY}+C2)}{({\mu }_X^2+{\mu }_Y^2+C1)({\sigma }_X^2+{\sigma }_Y^2+C2)}$

   $\mu$ 是均值，$\sigma$ 是方差，C1和C2是稳定除法的变量。

   $\text{SSIMLoss}(X,Y)=1?\frac{\text{SSIM}(X,Y)}{2}$

3. 对抗损失：对抗损失使用鉴别器模型的输出计算，鉴别器模型负责将输入图像分类为真实或伪造。

   鉴别器模型的损失函数定义如下：

   $\text{AdvLoss}(Y,X)=?{\mathbb{E}}_Y[\log (1?D(Y,X))]?{\mathbb{E}}_X[\log (D(Y,X))]$

   $D(x_r,x_f)$ 是鉴别器模型给出的预测。

4. 感知损失：感知损失使用VGG19网络测量激活特征之间的距离，并使用MSE损失函数最小化该距离。

5. 分割模型的BCE损失：分割模型使用二元交叉熵损失训练。

   $\text{BCELoss}=?\frac{1}{N}{\sum }_{i=1}^N(x_{it?1}\log (x_{{\theta }_{it?1}})+(1?x_{it?1})\log (1?x_{{\theta }_{it?1}}))$

   N代表图像中的像素数。