机器学习（八） — K-means

model 5 — K-means

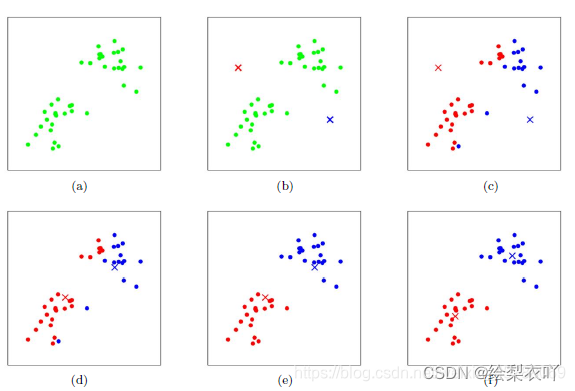
1 definition

1. randomly initialize K cluster centroids ${\mu }_1,{\mu }_2,?$
2. repeat:
   • assign each point to its closest centroid $\mu$
   • recompute the centroids(average of the closest point)

2 optimazation objective

1. $c^{(i)}$ = index of cluster to which example $x^{(i)}$ is currently assigned
2. ${\mu }_k$ = cluster centroid k
3. ${\mu }_{c^{(i)}}$ = cluster centroid of cluster to which example $x^{(i)}$ has been assigned

$$J=\frac{1}{m}\sum _{i=1}^m\Vert x^{(i)}?{\mu }_{c^{(i)}}\Vert$$

3 randomly initialization

for i = 1 to n(usually 50 to 1000)
	randomly initialize K-means
	run K-means
	compute cost function
	
pick set of clusters that give the lowest cost