[LeetCode周赛复盘] 第 379 场周赛20240107
发布时间:2024年01月07日
[LeetCode周赛复盘] 第 379 场周赛20240107
一、本周周赛总结
- 赛后半小时才做出T4 ,比赛时就没交
- T1 模拟。
- T2 BFS。
- T3 集合论。
- T4 DP+记忆化搜索。
100170. 对角线最长的矩形的面积
1. 题目描述
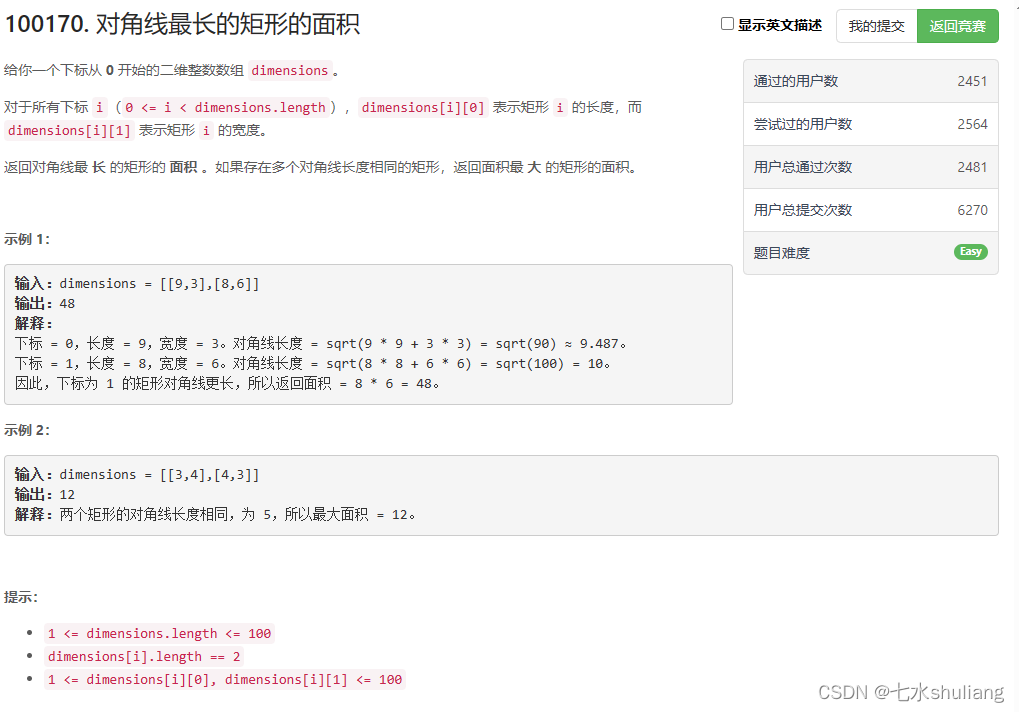
2. 思路分析
- 找到最长的对角线,用勾股定理,其实算自定义排序。
3. 代码实现
class Solution:
def areaOfMaxDiagonal(self, dimensions: List[List[int]]) -> int:
ans = [0,0]
for x,y in dimensions:
ans = max(ans,[x*x+y*y,x*y])
return ans[1]
100187. 捕获黑皇后需要的最少移动次数
1. 题目描述
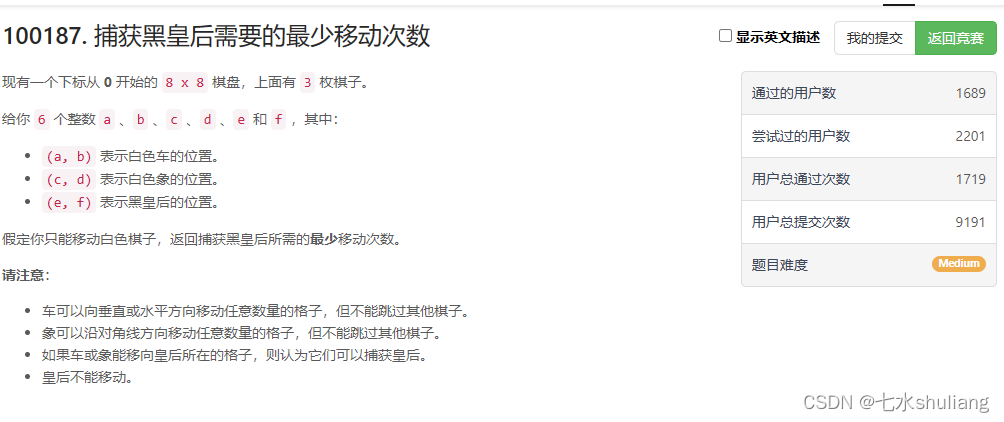
2. 思路分析
贪心讨论怎么想都很难,数据量很小,干脆BFS。
- 由于皇后是不动的,因此状态是4维:车和象的坐标。
- 模拟车和象向四个方向移动的状态,遇到出界或者白棋则停下(break);遇到皇后就返回答案。
3. 代码实现
DIRS1 = [(0,1),(0,-1),(1,0),(-1,0)]
DIRS2 = [(1,1),(1,-1),(-1,1),(-1,-1)]
class Solution:
def minMovesToCaptureTheQueen(self, a: int, b: int, c: int, d: int, e: int, f: int) -> int:
a -= 1
b-=1
c-=1
d-=1
e-=1
f-=1
q = [(a,b,c,d)]
vis = set(q)
ans = 1
while q:
nq = []
for a,b,c,d in q:
for dx,dy in DIRS1:
cnt = 0
while True:
cnt += 1
x,y = a+dx*cnt,b+dy*cnt
if not (0<=x<8 and 0<=y<8) or x == c and y == d:
break
if x == e and y == f:
return ans
v = (x,y,c,d)
if v not in vis:
vis.add(v)
nq.append(v)
for dx,dy in DIRS2:
cnt = 0
while True:
cnt += 1
x,y = c+dx*cnt,d+dy*cnt
if not (0<=x<8 and 0<=y<8) or x == a and y == b:
break
if x == e and y == f:
return ans
v = (a,b,x,y)
if v not in vis:
vis.add(v)
nq.append(v)
ans += 1
q = nq
100150. 移除后集合的最多元素数
1. 题目描述
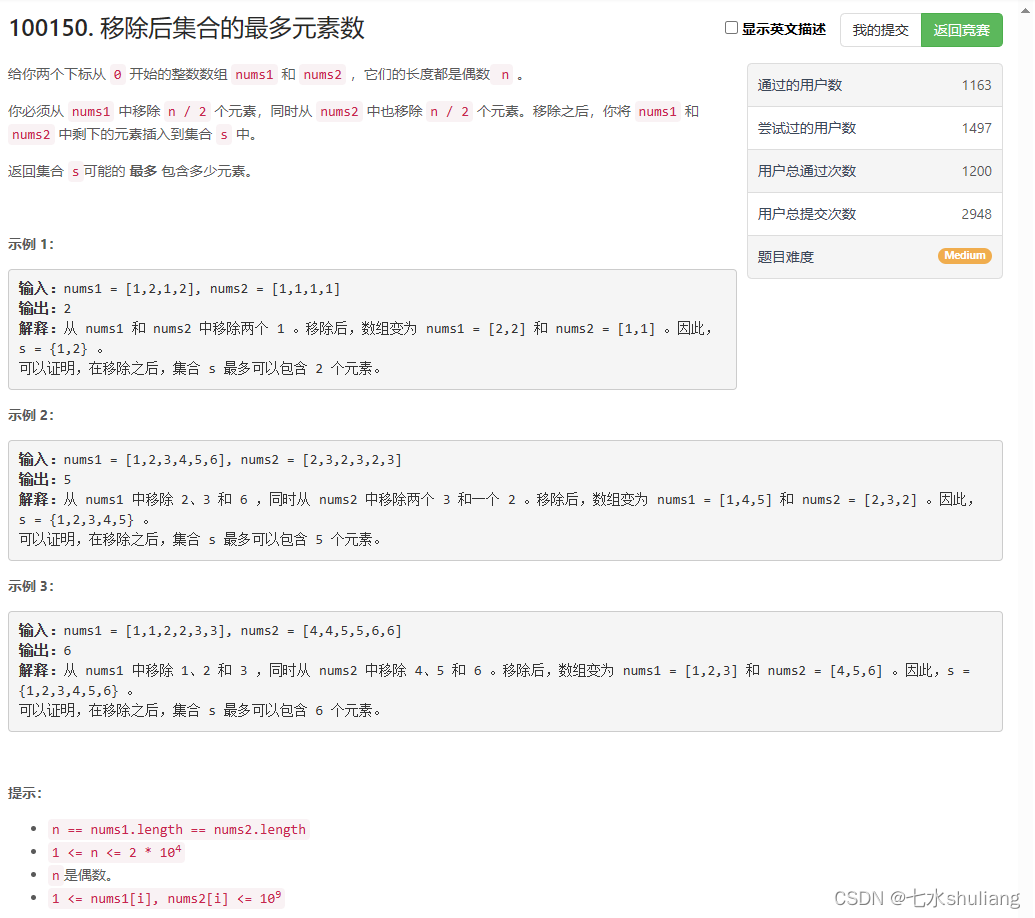
2. 思路分析
- 正难则反,讨论每个数组保留n/2个元素。
- 令a = set(nums1),b=set(nums2)
- x,y,z分别表示a-b(a独有的元素),b-a(b独有),a&b(共有元素)
- 那么最后a中保留的元素显然可以优先从x中取,即len(x)个(不超过n/2)。b中保留的元素优先从y取。
- 最后如果还能取,则从共有的部分取,这部分可以任意补充到左右两边。
3. 代码实现
class Solution:
def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:
h = len(nums1)//2
n = len(nums1)
a,b = set(nums1),set(nums2)
x,y,z = len(a-b),len(b-a),len(a&b)
ans = min(h,x)+min(h,y)
ans += min(n-ans,z)
return ans
100154. 执行操作后的最大分割数量
1. 题目描述
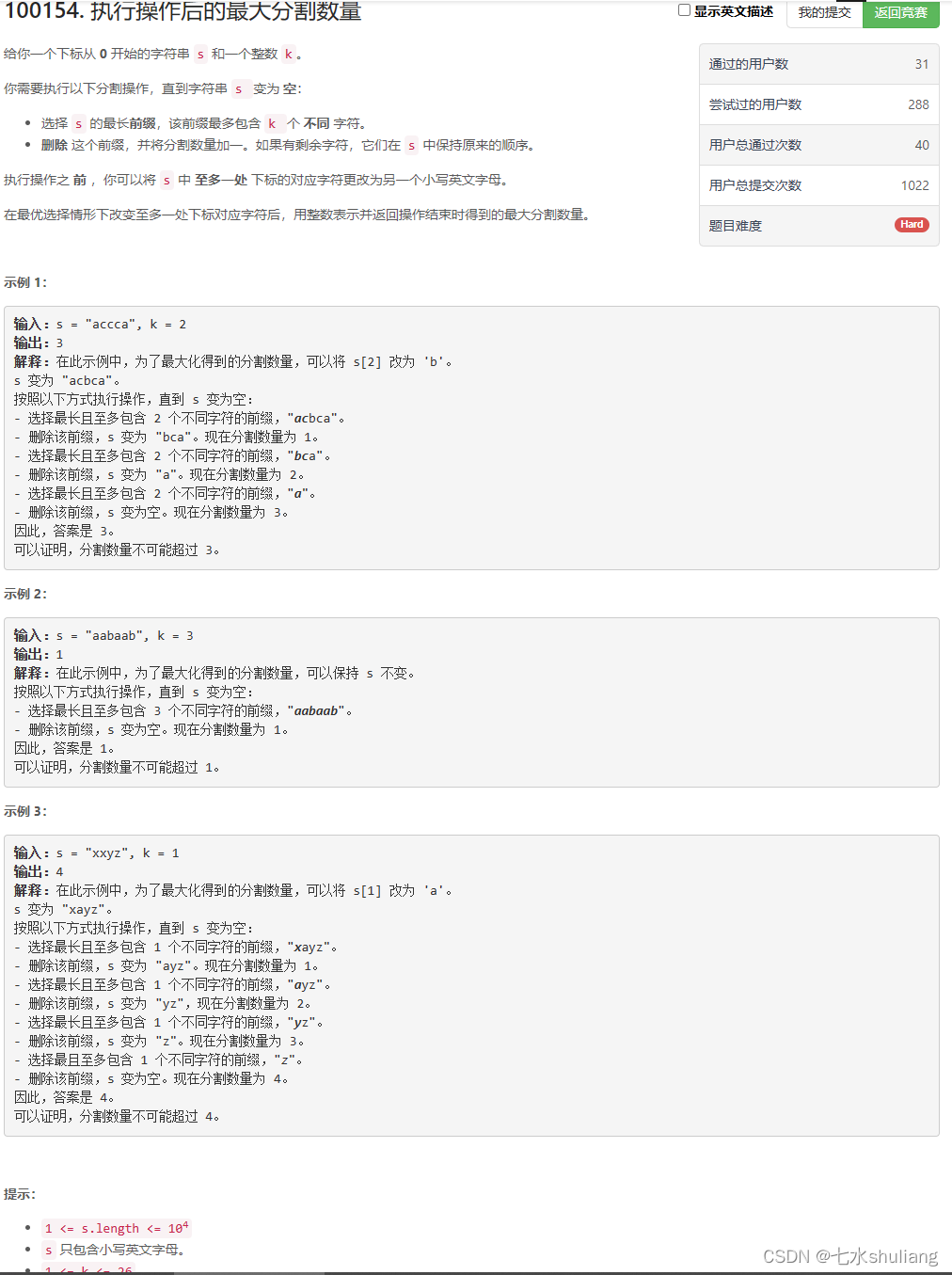
2. 思路分析
- 记忆化搜索,找子问题。
- 先做几个特判,方便后边编码:
- 当k==26,那么整个s只能作为一整段,因为不管怎么改,前缀都可以一直延伸到最后。这一段不会超过26个不同。
- 当k>len(set(s)),即即使给s中增加一个其不存在的字符,也只能持平k,那么无论怎么改,这一段同样不会超过k个元素。return 1。
- 若果k==1,为了后续写代码方便也特判:
- 不改变的情况下,显然ans 至少是 相邻相同分组数,(比如aaabbaa是3组)。
- 但可以通过一次操作,增加组数,最长组是2,改变一个,增加一组;最长组超过3,改变中间那个,增加2组。
- 特判之后,2<=k<=25,开始写记忆化搜索。
- 先手玩分析:从头开始延伸前缀,如果攒够k个不同的字符,则拆段,分析后边的段,这是子问题,且和前边的状态无关。
- 令f(i,chance,start)表示从i开始的后缀里,最多能拆多少段。其中chance表示还有几次修改机会,start表示s[i]的字符是谁。
- 那么从si开始用vis:set统计,假设当前把j加入集合,讨论集合内不同字符数量:
- 若len(vis)==k,即集合中已经有k个不同字符,那尝试拆段:
- 如果后一个字符不在vis中,则可以直接拆ans = 1 + f(j+1,chance,s[j+1]),注意,必须拆,这里拆完就要break了。
- 如果后一个字符在vis中,它本应和前缀作为同一段,因此需要修改,遍历26个字母,尝试改成一个不在vis中的字符:ans = 1 + f(j+1,0,c),注意chance要使用。
- 若len(vis)==k-1 且vis中有重复字符,则可以修改一个重复字符为一个不存在vis中的字符(注意k<=25,则一定可以修改为一个其它小写字母),使这段变成k,ans = 1+f(j+1,0,s[j+1]),但是注意,这里一定要保证s[j+1] 不在vis中,否则又要连上前一段。
- 若len(vis)==k,即集合中已经有k个不同字符,那尝试拆段:
- 实现时,由于会讨论s[j+1]这个位置,手动给s最后加一个‘*’作为哨兵。
3. 代码实现
class Solution:
def maxPartitionsAfterOperations(self, s: str, k: int) -> int:
n = len(s)
if k == 26: # k是26怎么改都是1组
return 1
if k > len(set(s)): # 一共k-1个不同字符,怎么改最多也只有k种字符
return 1
if k == 1:
f = [1]*n
for i in range(1,n):
if s[i] == s[i-1]:
f[i] += f[i-1]
ans = f.count(1)
mx = max(f)
if mx >= 3:
return ans + 2
if mx == 2:
return ans + 1
return ans
s += '*'
@cache
def f(i,chance,start):
if i == n:
return 0
vis = {start}
ans = 1
for j in range(i+1,n):
vis.add(s[j])
c = s[j+1]
if chance and c not in vis and len(vis) == k - 1 and j-i+1>=k:
ans = max(ans, 1 + f(j+1,0,c))
if chance and len(vis) == k and c in vis:
for z in range(26):
d = chr(ord('a')+z)
if d not in vis:
ans = max(ans, 1 + f(j+1,0,d))
if len(vis) == k and c not in vis:
ans = max(ans, 1 + f(j+1,chance,c))
break
return ans
return f(0,1,s[0])
参考链接
文章来源:https://blog.csdn.net/liuliangcan/article/details/135440614
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- maven运行时报错“java.lang.NoClassDefFoundError:sun/misc/BASE64Decoder”
- 用 Python 制作可视化 GUI 界面,一键实现自动分类管理文件!
- WebRTC AEC回声消除算法拆解
- 【一分钟】ThinkPHP v6.0 (poc-yaml-thinkphp-v6-file-write)环境复现及poc解析
- 2023APMCM亚太数学建模C题 - 中国新能源汽车的发展趋势(2)
- Pingcode和HelpLook对比:哪一个知识库工具更好?
- JavaFX入门
- git 使用 submodule 如何指定分支
- 微信小程序+前后端开发学习材料
- Vi文本编辑器如何使用,这里有详细步骤