机器学习---聚类(原型聚类、密度聚类、层次聚类)
1. 原型聚类
原型聚类也称为“基于原型的聚类” (prototype-based clustering),此类算法假设聚类结构能通过一
组原型刻画。算法过程:通常情况下,算法先对原型进行初始化,再对原型进行迭代更新求解。著
名的原型聚类算法:k均值算法、学习向量量化算法、高斯混合聚类算法。
给定数据集![]() ,k均值算法针对聚类所得簇划分
,k均值算法针对聚类所得簇划分![]() ,最
,最
小化平方误差:![]()
其中,![]() 是簇
是簇![]() 的均值向量。值在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,值越
的均值向量。值在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,值越
小,则簇内样本相似度越高。
1.1 K均值
K均值算法:算法流程(迭代优化):初始化每个簇的均值向量,repeat:(更新)簇划分;计算
每个簇的均值向量,until:当前均值向量均未更新。
算法伪代码:

k均值算法实例:?
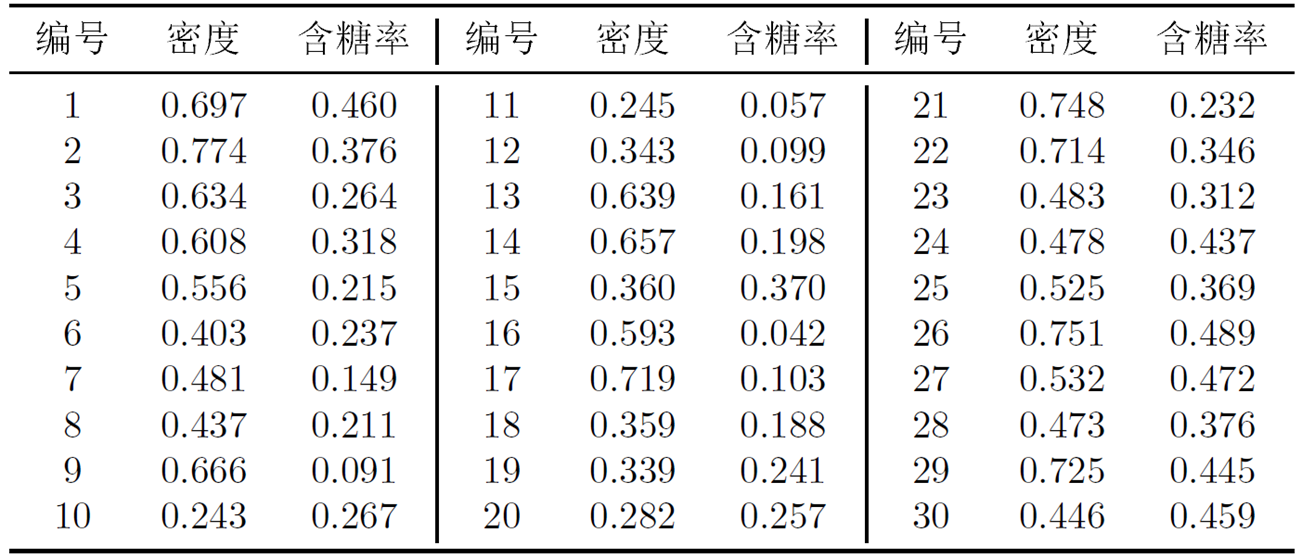
接下来以表9-1的西瓜数据集4.0为例,来演示k均值算法的学习过程。将编号为i的样本称为![]() ?????
?????
假定聚类簇数k =3,算法开始时,随机选择3个样本![]() 作为初始均值向量,即
作为初始均值向量,即
![]() ?
?
考察样本![]() ,它与当前均值向量
,它与当前均值向量![]() ,的距离分别为0.369,0.506,
,的距离分别为0.369,0.506,
0.166,因此![]() 将被划入簇
将被划入簇![]() 中。类似的,对数据集中的所有样本考察一遍后,可得当前簇划分
中。类似的,对数据集中的所有样本考察一遍后,可得当前簇划分
为![]()
![]()
![]()
于是,可以从分别求得新的均值向量:
![]()
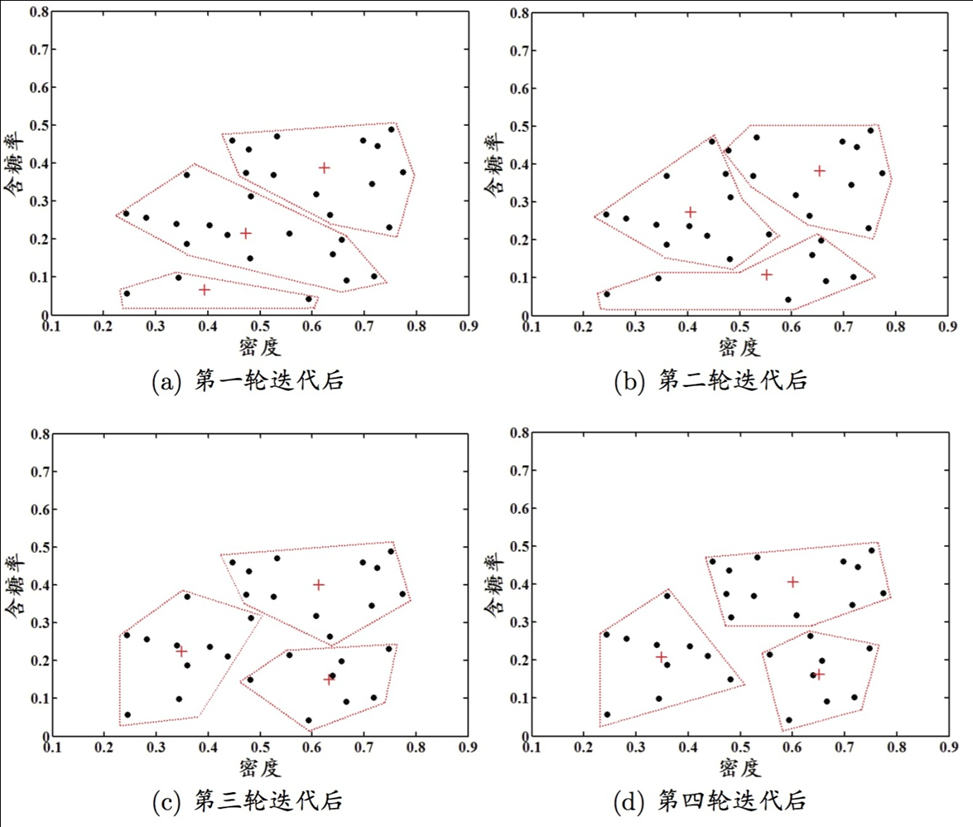
不断重复上述过程,如下图所示。
聚类结果:
1.2?学习向量量化
学习向量量化(Learning Vector Quantization, LVQ):
与一般聚类算法不同的是,LVQ假设数据样本带有类别标记,学习过程中利用样本的这些监督信息
来辅助聚类。给定样本集![]() ,LVQ的目标是学得一组n维
,LVQ的目标是学得一组n维
原型向量![]() ,每个原型向量代表一个聚类簇。常用于发现类别的“子类”结构。?
,每个原型向量代表一个聚类簇。常用于发现类别的“子类”结构。?

聚类效果:

1.3 高斯混合聚类?
与k均值、LVQ用原型向量来刻画聚类结构不同,高斯混合聚类 (Mixture-of-Gaussian)采用概率
模型来表达聚类原型:
多元高斯分布的定义:
对n维样本空间中的随机向量x,若x服从高斯分布,其概率密度函数为
![]()
其中![]() 是n维均值向量,?
是n维均值向量,?![]() 是
是![]() 的协方差矩阵。也可将概率密度函数记作
的协方差矩阵。也可将概率密度函数记作![]() 。
。
高斯混合分布的定义:
 该分布由K个混合分布组成,每个分布对应一个高斯分布。其中, ?
该分布由K个混合分布组成,每个分布对应一个高斯分布。其中, ?
与![]() 是第
是第![]() 个高斯混合成分的参数。而
个高斯混合成分的参数。而![]() 为相应的“混合系数”,且
为相应的“混合系数”,且![]() 。
。
假设样本的生成过程由高斯混合分布给出:首先,根据a1,a2,···,ak定义的先验分布选择高斯
混合成分,其中ai为选择第i个混合成分的概率;然后,根据被选择的混合成分的概率密度函数进行
采样,从而生成相应的样本。
模型求解:最大化(对数)似然
![]()

?令![]() 得
得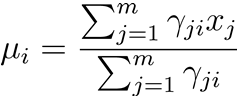 ,令
,令![]() 得
得

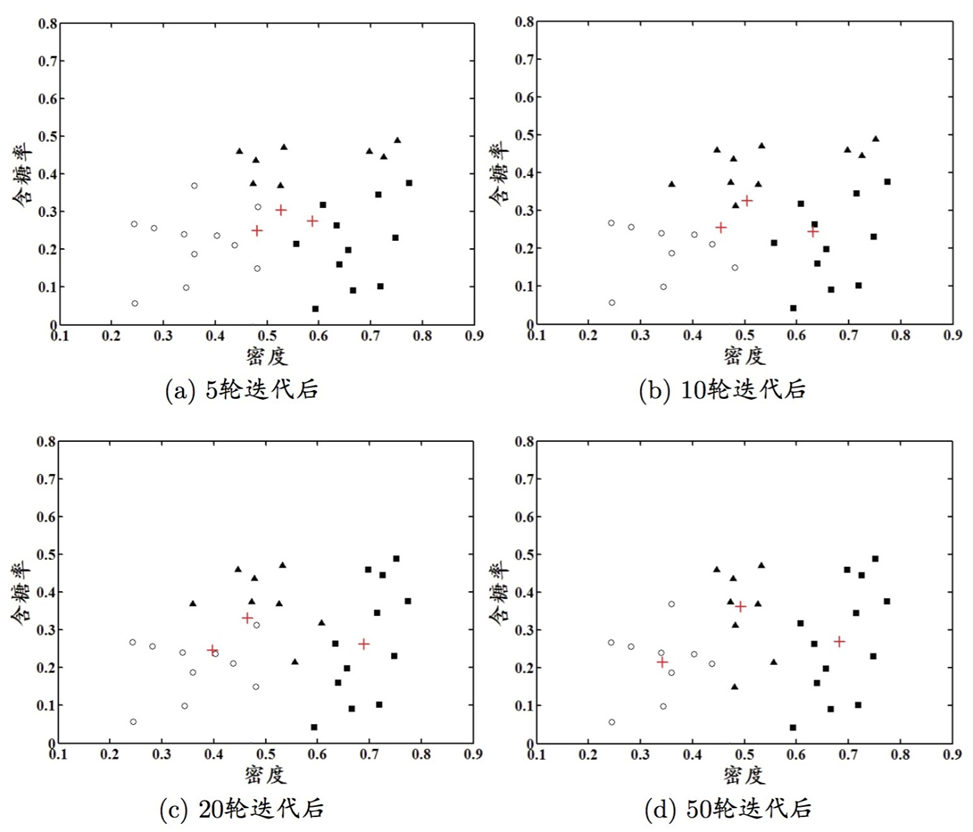
聚类结果:
2. 密度聚类
密度聚类也称为“基于密度的聚类” (density-based clustering)。此类算法假设聚类结构能通过样本
分布的紧密程度来确定。通常情况下,密度聚类算法从样本密度的角度来考察样本之间的可连接
性,并基于可连接样本不断扩展聚类簇来获得最终的聚类结果。接下来介绍DBSCAN这一密度聚
类算法。
DBSCAN算法:基于一组“邻域”参数![]() 来刻画样本分布的紧密程度。
来刻画样本分布的紧密程度。
基本概念:
![]() 邻域:对样本
邻域:对样本![]() ,其
,其![]() 邻域包含样本集D中与
邻域包含样本集D中与![]() 的距离不大于
的距离不大于![]() 的样本;
的样本;
核心对象:若样本![]() 的
的![]() 邻域至少包含MinPts个样本,则该样本点为一个核心对象;
邻域至少包含MinPts个样本,则该样本点为一个核心对象;
密度直达:若样本![]() 位于样本
位于样本![]() 的
的![]() 邻域中,且
邻域中,且![]() 是一个核心对象,则称样本
是一个核心对象,则称样本![]() 由
由![]() 密度直
密度直
达;
密度可达:对样本![]() 与
与![]() ,若存在样本序列
,若存在样本序列![]() ,其中
,其中![]() ,且
,且![]()
![]() 由
由![]() 密度直达,则该两样本密度可达; ?????
密度直达,则该两样本密度可达; ?????
密度相连:对样本![]() 与
与![]() ,若存在样本??? 使得两样本均由
,若存在样本??? 使得两样本均由![]() 密度可达,则称该两样本密度相
密度可达,则称该两样本密度相
连。
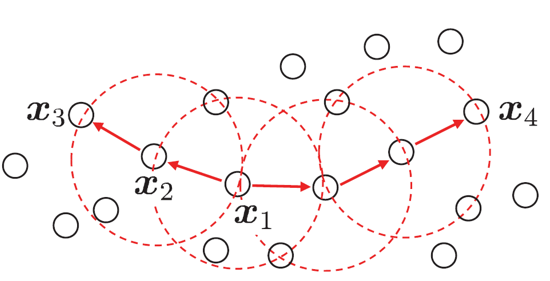
一个例子:令MinPts=3,则虚线显示出![]() 邻域。x1是核心对象。x2由x1密度直达。x3由x1密度可
邻域。x1是核心对象。x2由x1密度直达。x3由x1密度可
达。x3与x4密度相连。
对“簇”的定义:由密度可达关系导出的最大密度相连样本集合。
对“簇”的形式化描述:给定领域参数,簇是满足以下性质的非空样本子集:连接性:
![]() xi与xj密度相连,最大性:
xi与xj密度相连,最大性:![]() ,xi与xj密度可达
,xi与xj密度可达![]()
BBSAN算法伪代码:

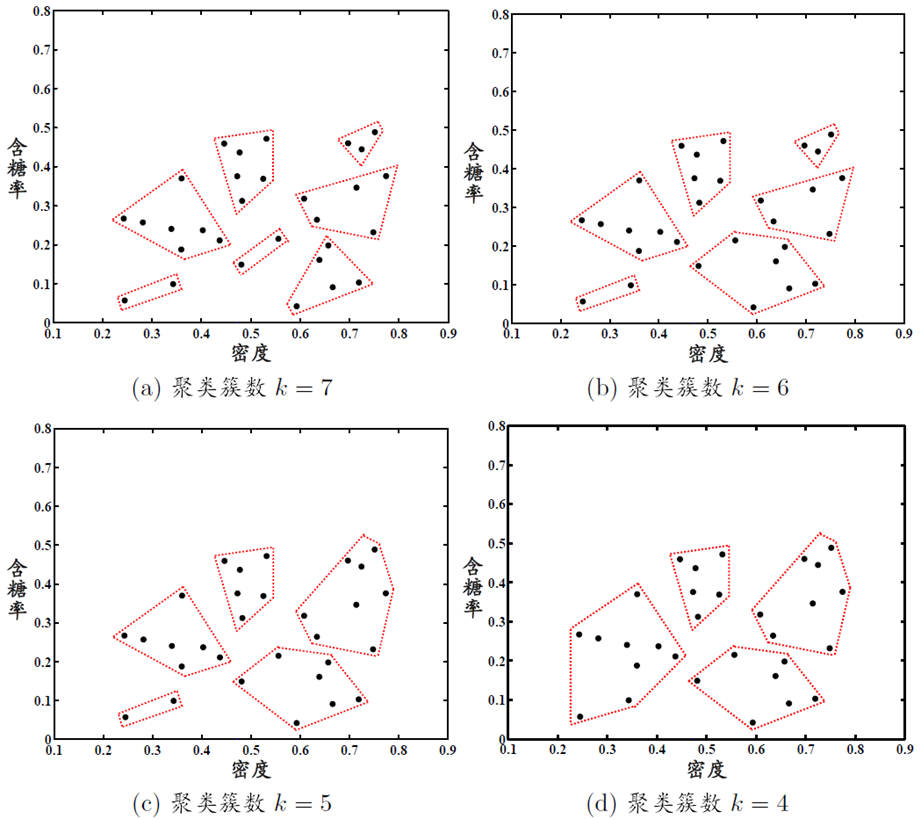
聚类效果:

3. 层次聚类?
层次聚类在不同层次对数据集进行划分,从而形成树形的聚类结构。数据集划分既可采用“自底向
上”的聚合策略,也可采用“自顶向下”的分拆策略。
AGNES算法(自底向上的层次聚类算法):首先,将样本中的每一个样本看做一个初始聚类簇,
然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直到达到预设
的聚类簇的个数。
两个聚类簇![]() 和
和![]() 的距离,可以有3种度量方式。
的距离,可以有3种度量方式。
最小距离:![]()
最大距离:![]()
平均距离:
AGNES算法树状图:

AGNES算法伪代码:?

AGNES算法聚类效果:?
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!