【线性代数】期末速通!
1. 行列式的性质
1.1 求一个行列式的值
特殊地,对角线左下全为0,结果为对角线乘积。行 r 列 c
1.2 性质
- 某行(列)加上或减去另一行(列)的几倍,行列式不变
- 某行(列)乘 k,等于 k 乘此行列式
- 互换两行(列),行列式变号
2. 行列式的计算及应用
见书 P22,P18
2.1 公式应用
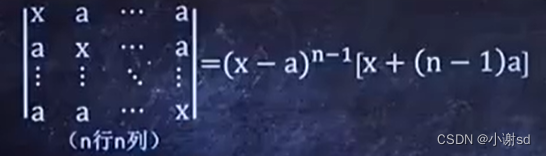
2.2 公式应用
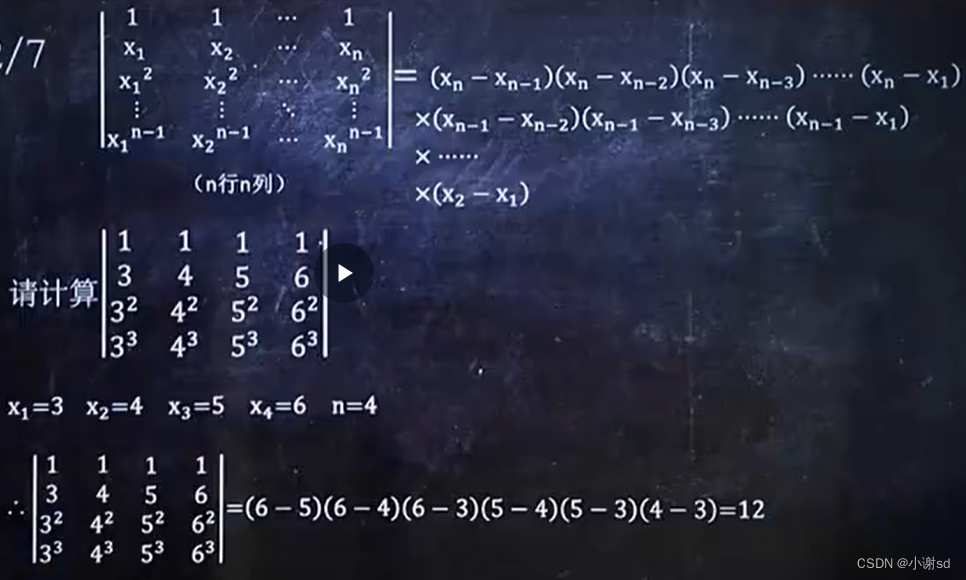
2.3 性质应用
①两行(列)相同或成比例时,行列式为0
②某行(列)为两项相加减时,行列式可拆成两个行列式相加减

2.4 求余子式(M)、代数余子式(A)


2.5 公式应用

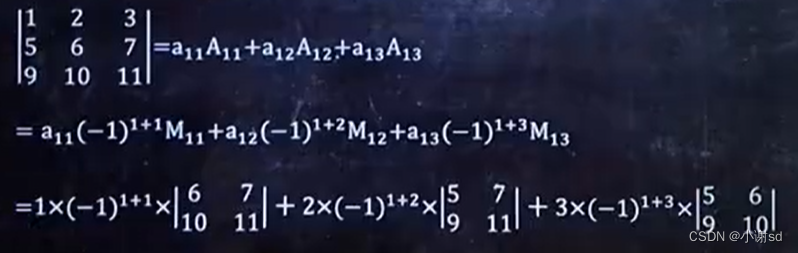
2.6 多个 A 或 M 相加减

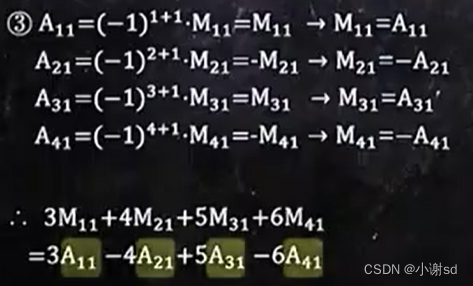
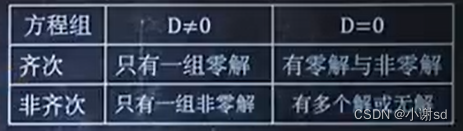
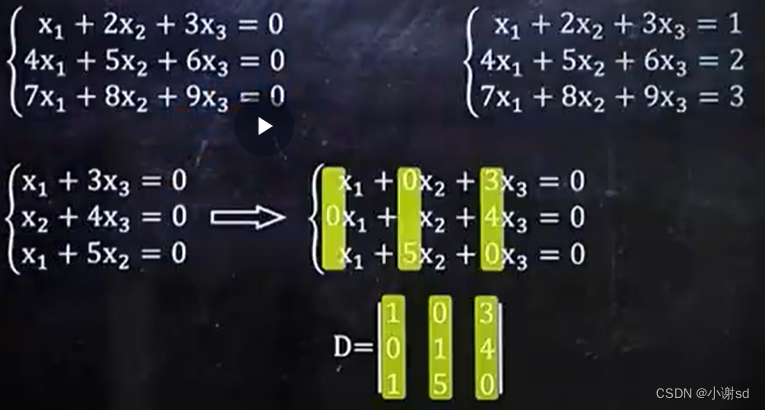
2.7 给一个方程组,判断其解的情况
3. 矩阵的运算上
3.1 矩阵加减

3.2 矩阵相乘
前行乘后列
结果行数等于前项,结果列数等于后项

特殊情况:


3.3 矩阵取绝对值

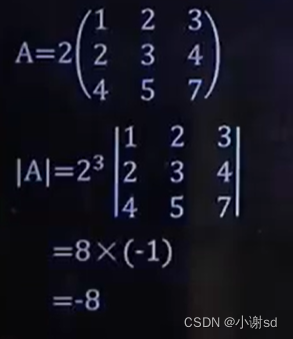

| A ^-1 | = | A | ^-1
行矩阵或者列矩阵的行列式的值就是各个数相乘。
对角矩阵是一个主对角线之外的元素皆为0的矩阵,常写为diag(a1,a2,…,an) 。

4. 矩阵的运算下
4.1 转置
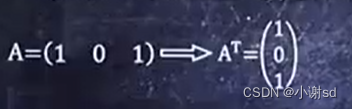
先用行乘列,简化运算。
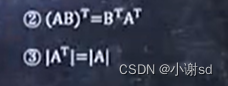
4.2 证明矩阵可逆


4.3 求逆矩阵


A 和 E 同时进行变换。
4.4 公式应用

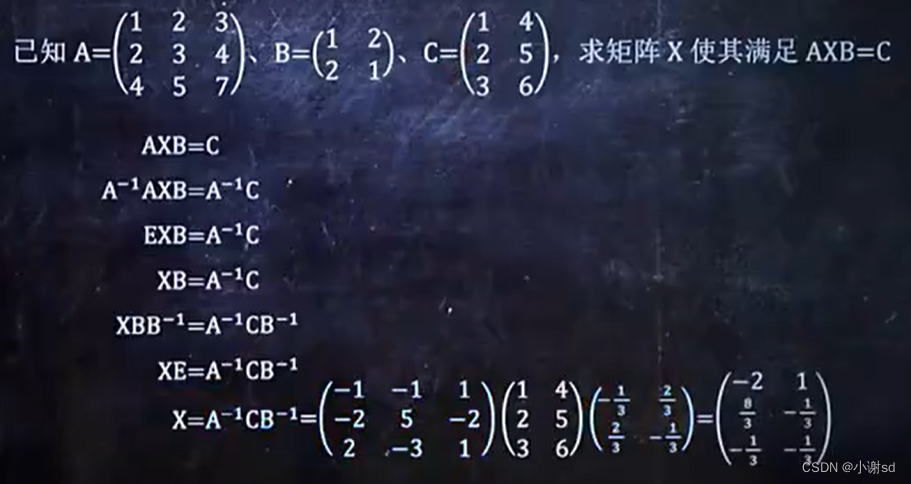
4.5 公式应用


4.6 求矩阵的秩或未知数
对矩阵进行行变换,是下行左端的0比上行多,直到下面行全为0为止。

秩为不全为0的行数。

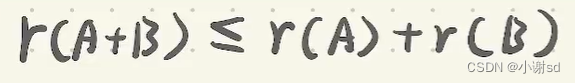
一个矩阵(非零)和它的转置矩阵相乘的积的秩为 1。零矩阵时为零。

5. 向量组与线性空间
5.1 判断某向量是否可以由某向量组线性表示

5.2 判断某个向量组是否线性相关


5.3 已知三维向量空间的一组基底,求某一向量在此基底下的坐标

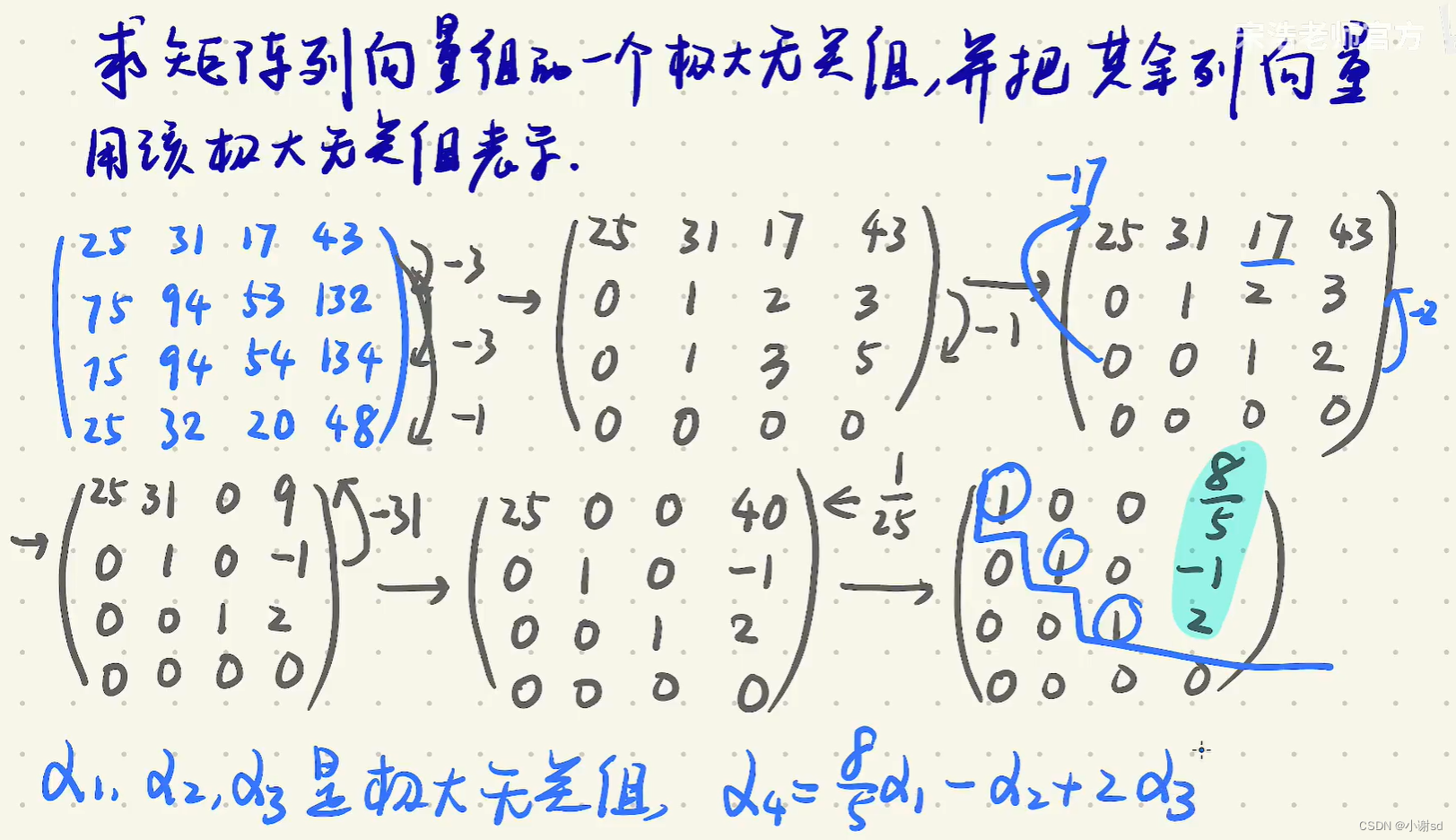
5.4 求几个行向量的极大无关组

操作步骤里面只有第一行和第四行做过交换,因此把前面的序号从1,2,3,4变为4,2,3,1。

6. 解方程组
6.1 判断方程组解的情况



6.2 解方程组(通解)

第②步:因为秩为3,所以将矩阵的前三行前三列的对角线变为1,其他变为0。

6.3 求方程组的通解、特解、基础解系
通解即为上述 6.2 中解出的方程组的解。
特解即为将 k 附任意值,得出的解。
基础解系是 k 后面的矩阵:

6.4 已知某方程组的多个特解,求某齐次方程组的通解
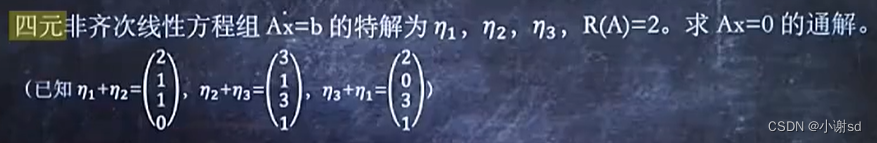
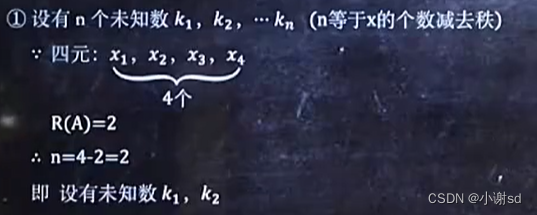

X1和X2不成比例就是线性无关。
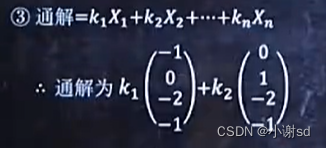
6.5 已知某方程组的多个特解,求某非齐次方程组的通解

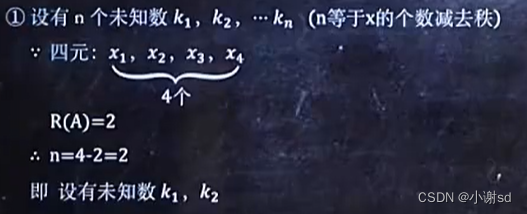


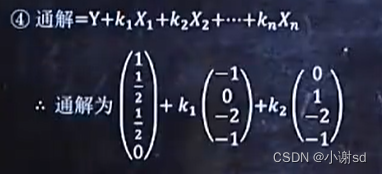
通解 = Ax=b 的一个特解 + 导出组的基础解系的线性组合

6.6 判断解集合中线性无关的解向量个数

7. 方阵对角化及其应用
7.1 规范正交化

比如:
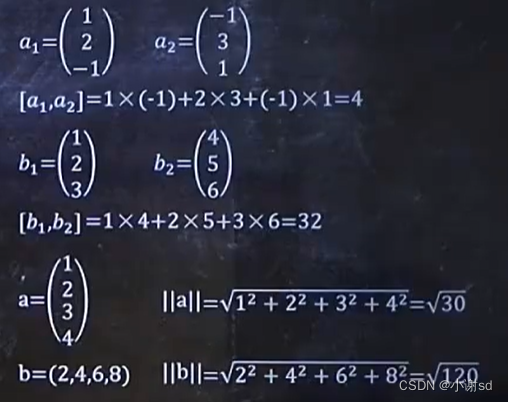

7.2 求矩阵的特征值


7.3 求矩阵的特征向量

先求特征值。

7.4 判断方阵是否与对角阵相似


7.5 求方阵对应的对角阵及可逆变换矩阵


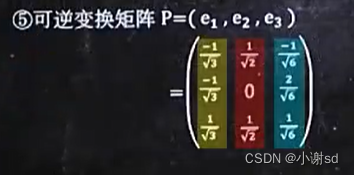
7.6 已知条件,求关于 A 的复杂式子
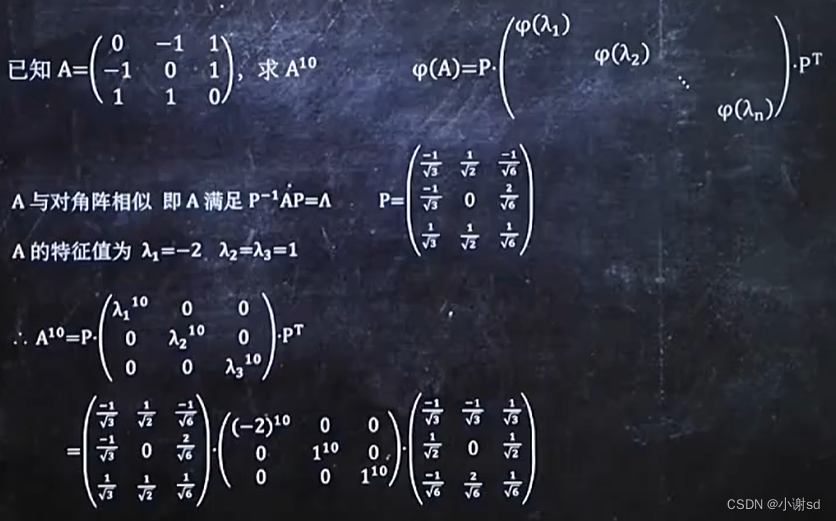
8. 二次型
8.1 求二次型对应的系数矩阵

8.2 把二次型化成标准型

8.3 把二次型化成规范形

8.4 用配方法把二次型化成标准型

8.5 判断二次型的正定性
系数矩阵的顺序主子式均大于 0 时,该二次型正定。

8.6 二次型为正定的等价条件

满足任意一条即可。
9. 其他题型
9.1 化为最简形矩阵
行最简型:①画楼梯②非零行首个一(也就是阶梯处)所在的列其他数都为零
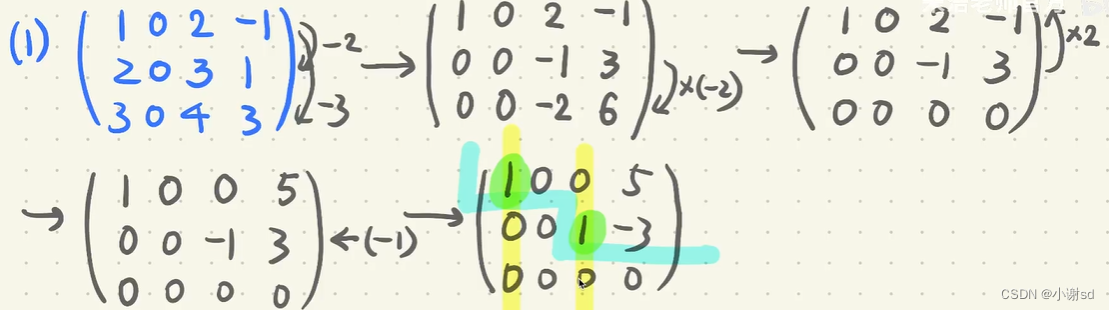
此题型有时答案可能不唯一。

(A矩阵的逆可以理解为 1 / A)

9.2 判断一个矩阵是否可逆
证明一个矩阵可逆的方法有5种:
(1)看这个矩阵的行列式值是否为0,若不为0,则可逆;
(2)看这个矩阵的秩是否为n,若为n,则矩阵可逆;
(3)定义法:若存在一个矩阵B,使矩阵A使得AB=BA=E,则矩阵A可逆,且B是A的逆矩阵;
(4)对于齐次线性方程AX=0,若方程只有零解,那么这个矩阵可逆,反之若有无穷解则矩阵不可逆;
(5)对于非齐次线性方程AX=b,若方程只有特解,那么这个矩阵可逆,反之若有无穷解则矩阵不可逆。
9.3 判断矩阵是否相似合同

9.4 矩阵消去律
消去左矩阵需要左矩阵满秩,消去右矩阵需要右矩阵满秩。
矩阵消去律详解
9.5 线性向量组相互表示
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 华清作业day50
- dw网页设计:布卡漫画官网(4个页面)HTML+CSS+JavaScript
- 一文搞懂 npm、cnpm、yarn、pnpm、npx、nvm 的区别
- 10款实用及摸鱼的前端特效源码分享(附图片效果及在线预览)
- windows2012 安装mysql5.7
- Obtect Detection,物体检测10年的发展,物体检测历史最佳网络
- 邮件群发:如何避免被拦截并提高送达率?
- 移动硬盘好还是移动u盘好?区别是什么
- 前端部署解决方案
- k8s-deployment initcontainers提前监测svc可用