代码随想录算法训练DAY27|回溯3

算法训练DAY27|回溯3

39. 组合总和

力扣题目链接

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

• 所有数字（包括 target）都是正整数。

• 解集不能包含重复的组合。

示例 1：

• 输入：candidates = [2,3,6,7], target = 7,

• 所求解集为： [ [7], [2,2,3] ]

示例 2：

• 输入：candidates = [2,3,5], target = 8,

• 所求解集为： [ [2,2,2,2], [2,3,3], [3,5] ]

题目中的无限制重复被选取，吓得我赶紧想想 出现0 可咋办，然后看到下面提示：1 <= candidates[i] <= 200，我就放心了。

本题和77.组合?，216.组合总和III?的区别是：本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制。

本题搜索的过程抽象成树形结构如下：

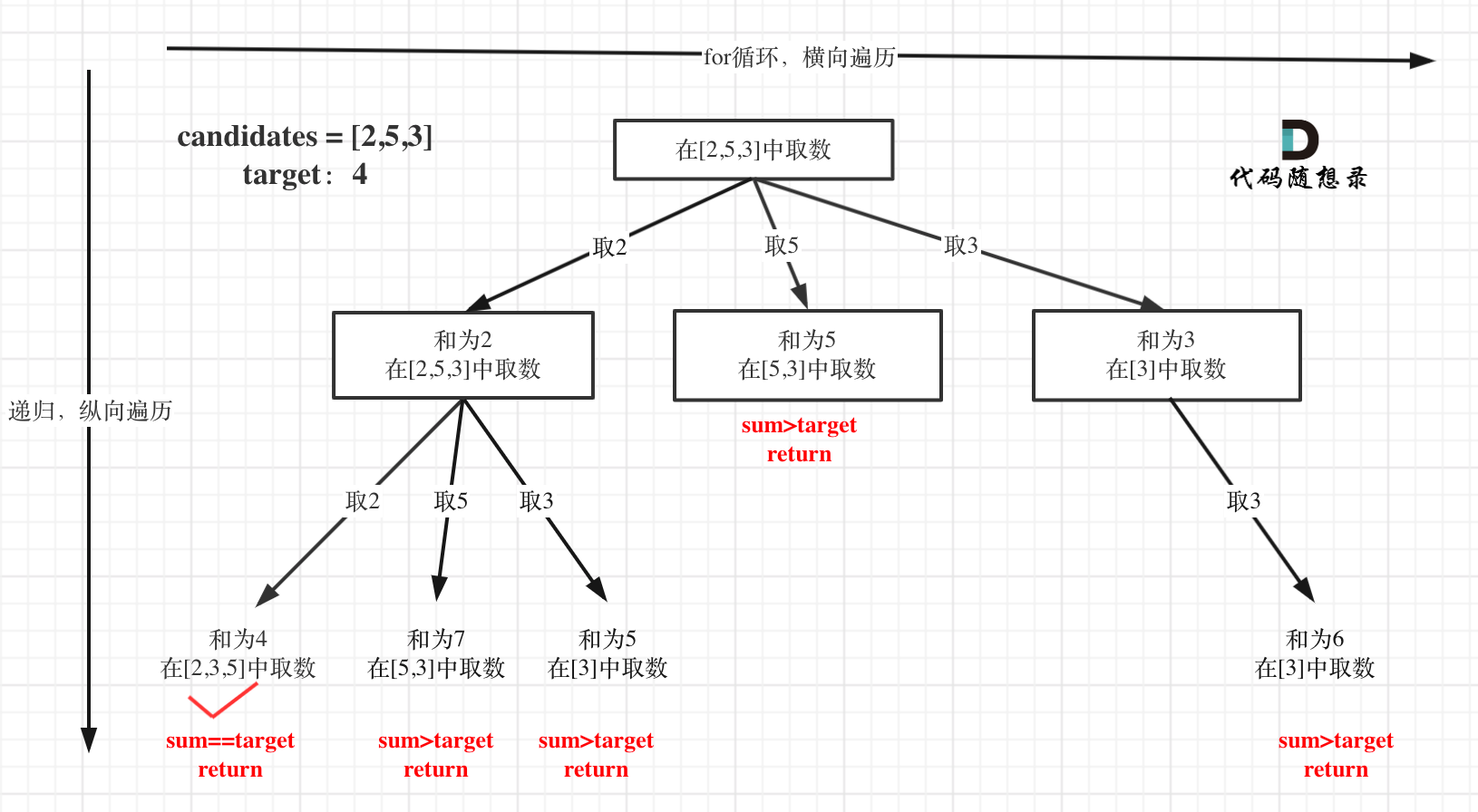
注意图中叶子节点的返回条件，因为本题没有组合数量要求，仅仅是总和的限制，所以递归没有层数的限制，只要选取的元素总和超过target，就返回！

#回溯三部曲

• 递归函数参数

这里依然是定义两个全局变量，二维数组result存放结果集，数组path存放符合条件的结果。（这两个变量可以作为函数参数传入）

首先是题目中给出的参数，集合candidates, 和目标值target。

此外我还定义了int型的sum变量来统计单一结果path里的总和，其实这个sum也可以不用，用target做相应的减法就可以了，最后如何target==0就说明找到符合的结果了，但为了代码逻辑清晰，我依然用了sum。

本题还需要startIndex来控制for循环的起始位置，对于组合问题，什么时候需要startIndex呢？

代码如下：

vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex)

• 递归终止条件

在如下树形结构中：

从叶子节点可以清晰看到，终止只有两种情况，sum大于target和sum等于target。

sum等于target的时候，需要收集结果，代码如下：

if (sum > target) {
 ? ?return;
}
if (sum == target) {
 ? ?result.push_back(path);
 ? ?return;
}

• 单层搜索的逻辑

单层for循环依然是从startIndex开始，搜索candidates集合。

如何重复选取呢，看代码，注释部分：

for (int i = startIndex; i < candidates.size(); i++) {
 ? ?sum += candidates[i];
 ? ?path.push_back(candidates[i]);
 ? ?backtracking(candidates, target, sum, i); // 关键点:不用i+1了，表示可以重复读取当前的数
 ? ?sum -= candidates[i]; ? // 回溯
 ? ?path.pop_back(); ? ? ? ?// 回溯
}

按照关于回溯算法，你该了解这些！?中给出的模板，不难写出如下C++完整代码：

// 版本一
class Solution {
private:
 ? ?vector<vector<int>> result;
 ? ?vector<int> path;
 ? ?void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
 ? ? ? ?if (sum > target) {
 ? ? ? ? ? ?return;
 ? ? ?  }
 ? ? ? ?if (sum == target) {
 ? ? ? ? ? ?result.push_back(path);
 ? ? ? ? ? ?return;
 ? ? ?  }
?
 ? ? ? ?for (int i = startIndex; i < candidates.size(); i++) {
 ? ? ? ? ? ?sum += candidates[i];
 ? ? ? ? ? ?path.push_back(candidates[i]);
 ? ? ? ? ? ?backtracking(candidates, target, sum, i); // 不用i+1了，表示可以重复读取当前的数
 ? ? ? ? ? ?sum -= candidates[i];
 ? ? ? ? ? ?path.pop_back();
 ? ? ?  }
 ?  }
public:
 ? ?vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
 ? ? ? ?result.clear();
 ? ? ? ?path.clear();
 ? ? ? ?backtracking(candidates, target, 0, 0);
 ? ? ? ?return result;
 ?  }
};

#剪枝优化

在这个树形结构中：

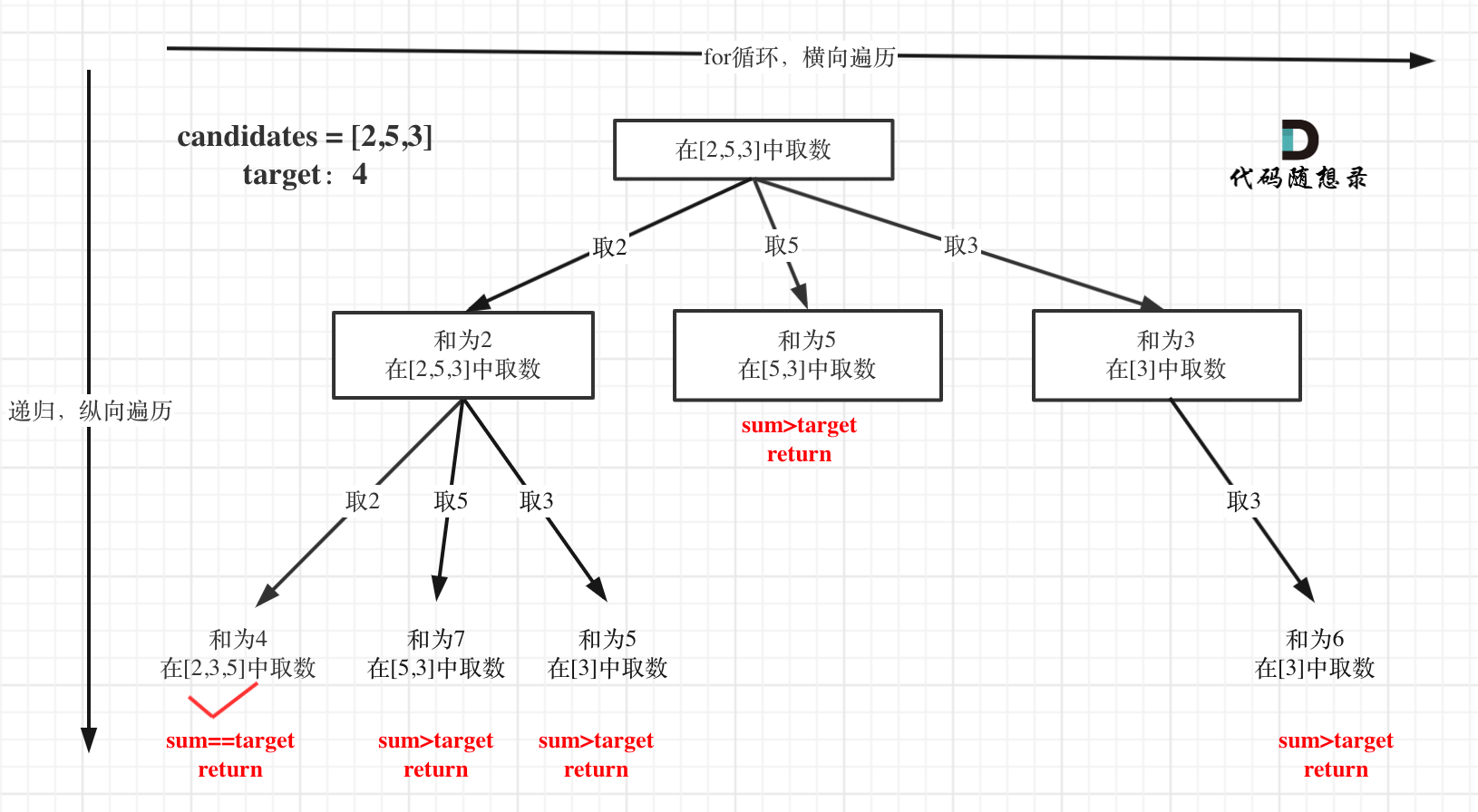
以及上面的版本一的代码大家可以看到，对于sum已经大于target的情况，其实是依然进入了下一层递归，只是下一层递归结束判断的时候，会判断sum > target的话就返回。

其实如果已经知道下一层的sum会大于target，就没有必要进入下一层递归了。

那么可以在for循环的搜索范围上做做文章了。

对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。

如图：

for循环剪枝代码如下：

for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)

整体代码如下：（注意注释的部分）

class Solution {
private:
 ? ?vector<vector<int>> result;
 ? ?vector<int> path;
 ? ?void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
 ? ? ? ?if (sum == target) {
 ? ? ? ? ? ?result.push_back(path);
 ? ? ? ? ? ?return;
 ? ? ?  }
?
 ? ? ? ?// 如果 sum + candidates[i] > target 就终止遍历
 ? ? ? ?for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
 ? ? ? ? ? ?sum += candidates[i];
 ? ? ? ? ? ?path.push_back(candidates[i]);
 ? ? ? ? ? ?backtracking(candidates, target, sum, i);
 ? ? ? ? ? ?sum -= candidates[i];
 ? ? ? ? ? ?path.pop_back();
?
 ? ? ?  }
 ?  }
public:
 ? ?vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
 ? ? ? ?result.clear();
 ? ? ? ?path.clear();
 ? ? ? ?sort(candidates.begin(), candidates.end()); // 需要排序
 ? ? ? ?backtracking(candidates, target, 0, 0);
 ? ? ? ?return result;
 ?  }
};

• 时间复杂度: O(n * 2^n)，注意这只是复杂度的上界，因为剪枝的存在，真实的时间复杂度远小于此

• 空间复杂度: O(target)

#总结

本题和我们之前讲过的77.组合?、216.组合总和III?有两点不同：

• 组合没有数量要求

• 元素可无限重复选取

针对这两个问题，我都做了详细的分析。

并且给出了对于组合问题，什么时候用startIndex，什么时候不用，并用17.电话号码的字母组合?做了对比。

最后还给出了本题的剪枝优化，这个优化如果是初学者的话并不容易想到。

在求和问题中，排序之后加剪枝是常见的套路！

可以看出我写的文章都会大量引用之前的文章，就是要不断作对比，分析其差异，然后给出代码解决的方法，这样才能彻底理解题目的本质与难点。

40.组合总和II

力扣题目链接

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明： 所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

• 示例 1:

• 输入: candidates = [10,1,2,7,6,1,5], target = 8,

• 所求解集为:

[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

• 示例 2:

• 输入: candidates = [2,5,2,1,2], target = 5,

• 所求解集为:

[
  [1,2,2],
  [5]
]

#思路

这道题目和39.组合总和 (opens new window)如下区别：

1. 本题candidates 中的每个数字在每个组合中只能使用一次。

2. 本题数组candidates的元素是有重复的，而39.组合总和 (opens new window)是无重复元素的数组candidates

最后本题和39.组合总和 (opens new window)要求一样，解集不能包含重复的组合。

本题的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合。

一些同学可能想了：我把所有组合求出来，再用set或者map去重，这么做很容易超时！

所以要在搜索的过程中就去掉重复组合。

很多同学在去重的问题上想不明白，其实很多题解也没有讲清楚，反正代码是能过的，感觉是那么回事，稀里糊涂的先把题目过了。

这个去重为什么很难理解呢，所谓去重，其实就是使用过的元素不能重复选取。 这么一说好像很简单！

都知道组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。

那么问题来了，我们是要同一树层上使用过，还是同一树枝上使用过呢？

回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。

所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

为了理解去重我们来举一个例子，candidates = [1, 1, 2], target = 3，（方便起见candidates已经排序了）

强调一下，树层去重的话，需要对数组排序！

选择过程树形结构如图所示：

与39.组合总和?相同，终止条件为 sum > target 和 sum == target。

代码如下：

if (sum > target) { // 这个条件其实可以省略
 ? ?return;
}
if (sum == target) {
 ? ?result.push_back(path);
 ? ?return;
}

sum > target 这个条件其实可以省略，因为在递归单层遍历的时候，会有剪枝的操作，下面会介绍到。

• 单层搜索的逻辑

这里与39.组合总和?最大的不同就是要去重了。

前面我们提到：要去重的是“同一树层上的使用过”，如何判断同一树层上元素（相同的元素）是否使用过了呢。

这块去重的逻辑很抽象，网上搜的题解基本没有能讲清楚的，如果大家之前思考过这个问题或者刷过这道题目，看到这里一定会感觉通透了很多！

class Solution {
private:
 ? ?vector<int> path;
 ? ?vector<vector<int>> result;
 ? ?void backtracking(int targetSum,int target, int startIndex, const vector<int>& candidates){
 ? ? ? ? ? ?if(targetSum>target){
 ? ? ? ? ? ? ? return;
 ? ? ? ? ?  }
 ? ? ? ? ? ?else{
 ? ? ? ? ? ? ? ?if(targetSum==target){
 ? ? ? ? ? ? ? ? ? ?result.push_back(path);
 ? ? ? ? ? ? ? ? ? ?return;
 ? ? ? ? ? ? ?  }
 ? ? ? ? ?  }
 ? ? ? ?for(int i=startIndex;i<candidates.size()&&targetSum+candidates[i]<=target;i++){
 ? ? ? ? ? ?// if(i>startIndex&&candidates[i]==candidates[i-1]){
 ? ? ? ? ? ?// ? ? continue;
 ? ? ? ? ? ?// }
 ? ? ? ? ? ?//相当于
 ? ? ? ? ? ?if(i>startIndex){
 ? ? ? ? ? ? ? ?if(candidates[i]==candidates[i-1]){
 ? ? ? ? ? ? ? ? ? ?continue;
 ? ? ? ? ? ? ?  }
 ? ? ? ? ?  }
 ? ? ? ? ? ?//error!!!!!!!
 ? ? ? ? ? ?// if(candidates[i]==candidates[i-1]&&i>startIndex){
 ? ? ? ? ? ?// ? ?  continue;
 ? ? ? ? ? ?// }
 ? ? ? ? ? ?targetSum+=candidates[i];
 ? ? ? ? ? ?path.push_back(candidates[i]);
 ? ? ? ? ? ?backtracking(targetSum,target,i+1,candidates);
 ? ? ? ? ? ?path.pop_back();
 ? ? ? ? ? ?targetSum-=candidates[i];
 ? ? ?  }
 ?  }
public:
 ? ?vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
 ? ? ? ?sort(candidates.begin(),candidates.end());
 ? ? ? ?backtracking(0,target,0,candidates);
 ? ? ? ?return result;
 ?  }
};

class Solution {
private:
 ? ?vector<vector<int>> result;
 ? ?vector<int> path;
 ? ?void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
 ? ? ? ?if (sum == target) {
 ? ? ? ? ? ?result.push_back(path);
 ? ? ? ? ? ?return;
 ? ? ?  }
 ? ? ? ?for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
 ? ? ? ? ? ?// 要对同一树层使用过的元素进行跳过
 ? ? ? ? ? ?if (i > startIndex && candidates[i] == candidates[i - 1]) {
 ? ? ? ? ? ? ? ?continue;
 ? ? ? ? ?  }
 ? ? ? ? ? ?sum += candidates[i];
 ? ? ? ? ? ?path.push_back(candidates[i]);
 ? ? ? ? ? ?backtracking(candidates, target, sum, i + 1); // 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次
 ? ? ? ? ? ?sum -= candidates[i];
 ? ? ? ? ? ?path.pop_back();
 ? ? ?  }
 ?  }
?
public:
 ? ?vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
 ? ? ? ?path.clear();
 ? ? ? ?result.clear();
 ? ? ? ?// 首先把给candidates排序，让其相同的元素都挨在一起。
 ? ? ? ?sort(candidates.begin(), candidates.end());
 ? ? ? ?backtracking(candidates, target, 0, 0);
 ? ? ? ?return result;
 ?  }
};

#总结

本题同样是求组合总和，但就是因为其数组candidates有重复元素，而要求不能有重复的组合，所以相对于39.组合总和?难度提升了不少。

关键是去重的逻辑，代码很简单，网上一搜一大把，但几乎没有能把这块代码含义讲明白的，基本都是给出代码，然后说这就是去重了，究竟怎么个去重法也是模棱两可。

所以Carl有必要把去重的这块彻彻底底的给大家讲清楚，就连“树层去重”和“树枝去重”都是我自创的词汇，希望对大家理解有帮助！

131.分割回文串

力扣题目链接

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]

#思路

本题这涉及到两个关键问题：

1. 切割问题，有不同的切割方式

2. 判断回文

相信这里不同的切割方式可以搞懵很多同学了。

这种题目，想用for循环暴力解法，可能都不那么容易写出来，所以要换一种暴力的方式，就是回溯。

一些同学可能想不清楚 回溯究竟是如何切割字符串呢？

我们来分析一下切割，其实切割问题类似组合问题。

例如对于字符串abcdef：

• 组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个.....。

• 切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段.....。

感受出来了不？

所以切割问题，也可以抽象为一棵树形结构，如图：

递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

此时可以发现，切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。

#回溯三部曲

• 递归函数参数

全局变量数组path存放切割后回文的子串，二维数组result存放结果集。 （这两个参数可以放到函数参数里）

本题递归函数参数还需要startIndex，因为切割过的地方，不能重复切割，和组合问题也是保持一致的。

代码如下：

vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
void backtracking (const string& s, int startIndex) {

• 递归函数终止条件

从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止条件。

那么在代码里什么是切割线呢？

在处理组合问题的时候，递归参数需要传入startIndex，表示下一轮递归遍历的起始位置，这个startIndex就是切割线。

所以终止条件代码如下：

void backtracking (const string& s, int startIndex) {
 ? ?// 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
 ? ?if (startIndex >= s.size()) {
 ? ? ? ?result.push_back(path);
 ? ? ? ?return;
 ?  }
}

• 单层搜索的逻辑

来看看在递归循环中如何截取子串呢？

在for (int i = startIndex; i < s.size(); i++)循环中，我们 定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。

首先判断这个子串是不是回文，如果是回文，就加入在vector<string> path中，path用来记录切割过的回文子串。

代码如下：

for (int i = startIndex; i < s.size(); i++) {
 ? ?if (isPalindrome(s, startIndex, i)) { // 是回文子串
 ? ? ? ?// 获取[startIndex,i]在s中的子串
 ? ? ? ?string str = s.substr(startIndex, i - startIndex + 1);
 ? ? ? ?path.push_back(str);
 ?  } else { ? ? ? ? ? ? ? ?// 如果不是则直接跳过
 ? ? ? ?continue;
 ?  }
 ? ?backtracking(s, i + 1); // 寻找i+1为起始位置的子串
 ? ?path.pop_back(); ? ? ? ?// 回溯过程，弹出本次已经添加的子串
}

注意切割过的位置，不能重复切割，所以，backtracking(s, i + 1); 传入下一层的起始位置为i + 1。

#判断回文子串

最后我们看一下回文子串要如何判断了，判断一个字符串是否是回文。

可以使用双指针法，一个指针从前向后，一个指针从后向前，如果前后指针所指向的元素是相等的，就是回文字符串了。

那么判断回文的C++代码如下：

 bool isPalindrome(const string& s, int start, int end) {
 ? ? for (int i = start, j = end; i < j; i++, j--) {
 ? ? ? ? if (s[i] != s[j]) {
 ? ? ? ? ? ? return false;
 ? ? ? ? }
 ? ? }
 ? ? return true;
 }

此时关键代码已经讲解完毕，整体代码如下（详细注释了）

根据Carl给出的回溯算法模板：

void backtracking(参数) {
 ? ?if (终止条件) {
 ? ? ? ?存放结果;
 ? ? ? ?return;
 ?  }
?
 ? ?for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
 ? ? ? ?处理节点;
 ? ? ? ?backtracking(路径，选择列表); // 递归
 ? ? ? ?回溯，撤销处理结果
 ?  }
}

不难写出如下代码：

class Solution {
private:
 ? ?vector<vector<string>> result;
 ? ?vector<string> path; // 放已经回文的子串
 ? ?void backtracking (const string& s, int startIndex) {
 ? ? ? ?// 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
 ? ? ? ?if (startIndex >= s.size()) {
 ? ? ? ? ? ?result.push_back(path);
 ? ? ? ? ? ?return;
 ? ? ?  }
 ? ? ? ?for (int i = startIndex; i < s.size(); i++) {
 ? ? ? ? ? ?if (isPalindrome(s, startIndex, i)) { ? // 是回文子串
 ? ? ? ? ? ? ? ?// 获取[startIndex,i]在s中的子串
 ? ? ? ? ? ? ? ?string str = s.substr(startIndex, i - startIndex + 1);
 ? ? ? ? ? ? ? ?path.push_back(str);
 ? ? ? ? ?  } else { ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?// 不是回文，跳过
 ? ? ? ? ? ? ? ?continue;
 ? ? ? ? ?  }
 ? ? ? ? ? ?backtracking(s, i + 1); // 寻找i+1为起始位置的子串
 ? ? ? ? ? ?path.pop_back(); // 回溯过程，弹出本次已经添加的子串
 ? ? ?  }
 ?  }
 ? ?bool isPalindrome(const string& s, int start, int end) {
 ? ? ? ?for (int i = start, j = end; i < j; i++, j--) {
 ? ? ? ? ? ?if (s[i] != s[j]) {
 ? ? ? ? ? ? ? ?return false;
 ? ? ? ? ?  }
 ? ? ?  }
 ? ? ? ?return true;
 ?  }
public:
 ? ?vector<vector<string>> partition(string s) {
 ? ? ? ?result.clear();
 ? ? ? ?path.clear();
 ? ? ? ?backtracking(s, 0);
 ? ? ? ?return result;
 ?  }
};

• 时间复杂度: O(n * 2^n)

• 空间复杂度: O(n^2)

#优化

动态规划，跳过