梯度下降算法
回顾
对于一个学习系统来说,我们需要找到最适合数据的模型,模型有很多,需要不断尝试,其中最简单的一个模型就是线性模型。


我们需要去找到一个w的取值,使得
(
y
^
?
y
)
2
(\widehat{y}-y)^2
(y
??y)2最小
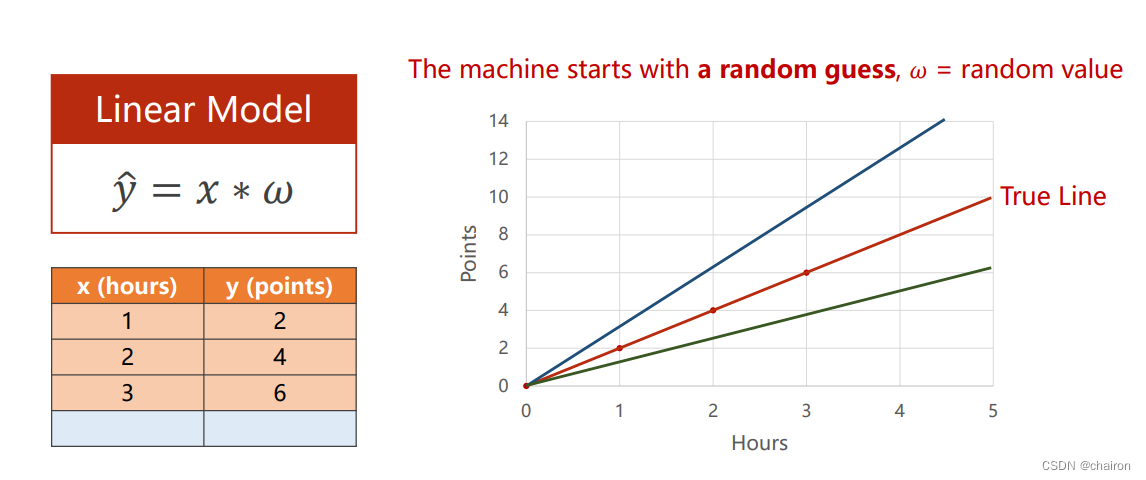
y
=
w
?
x
y=w*x
y=w?x可以采用穷举法求最优值w
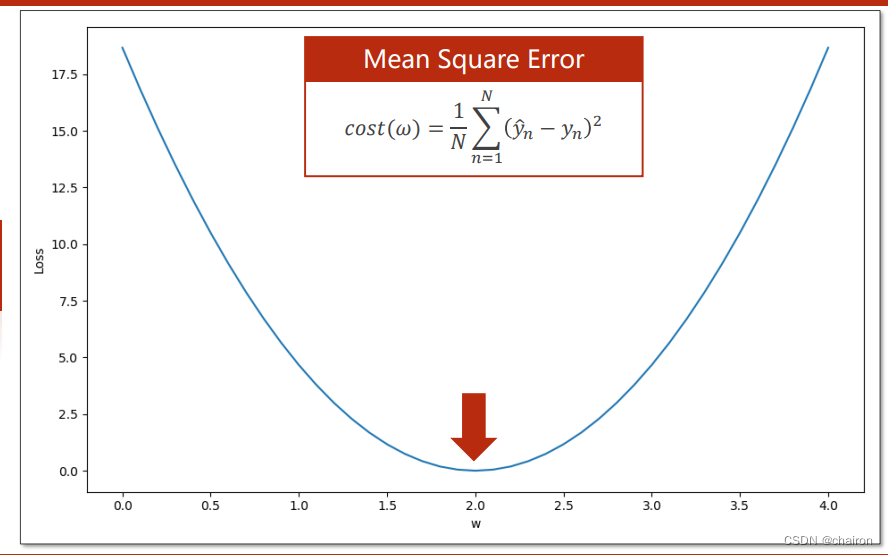
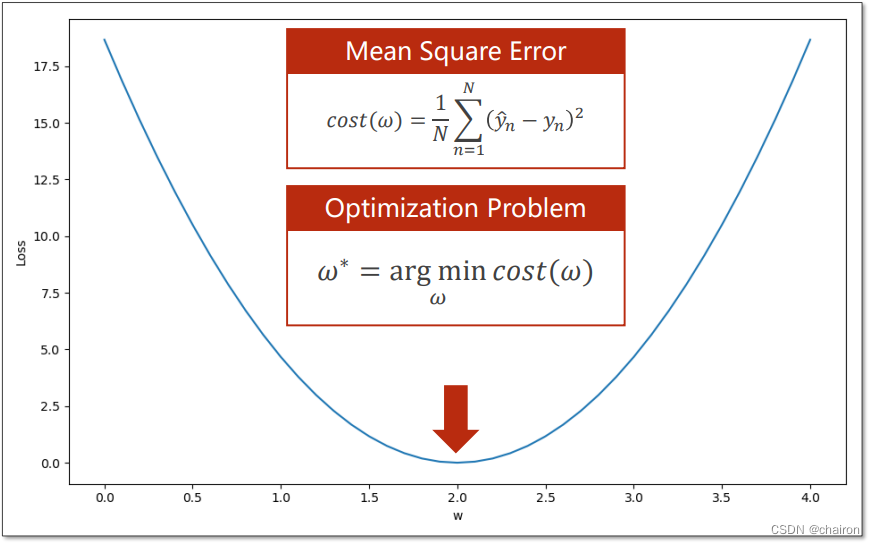
那么
y
=
w
1
?
x
1
+
w
2
?
x
2
y=w_1*x_1+w_2*x_2
y=w1??x1?+w2??x2?,如果采用穷举法来求最优值w,假设w取值为[0,100],计算量就是
10
0
2
100^2
1002……
假如有多个
w
i
w_i
wi?,那么计算量就是
10
0
n
100^n
100n.
优化问题
这种求得w的取值使得cost损失值最小的问题称为优化问题。
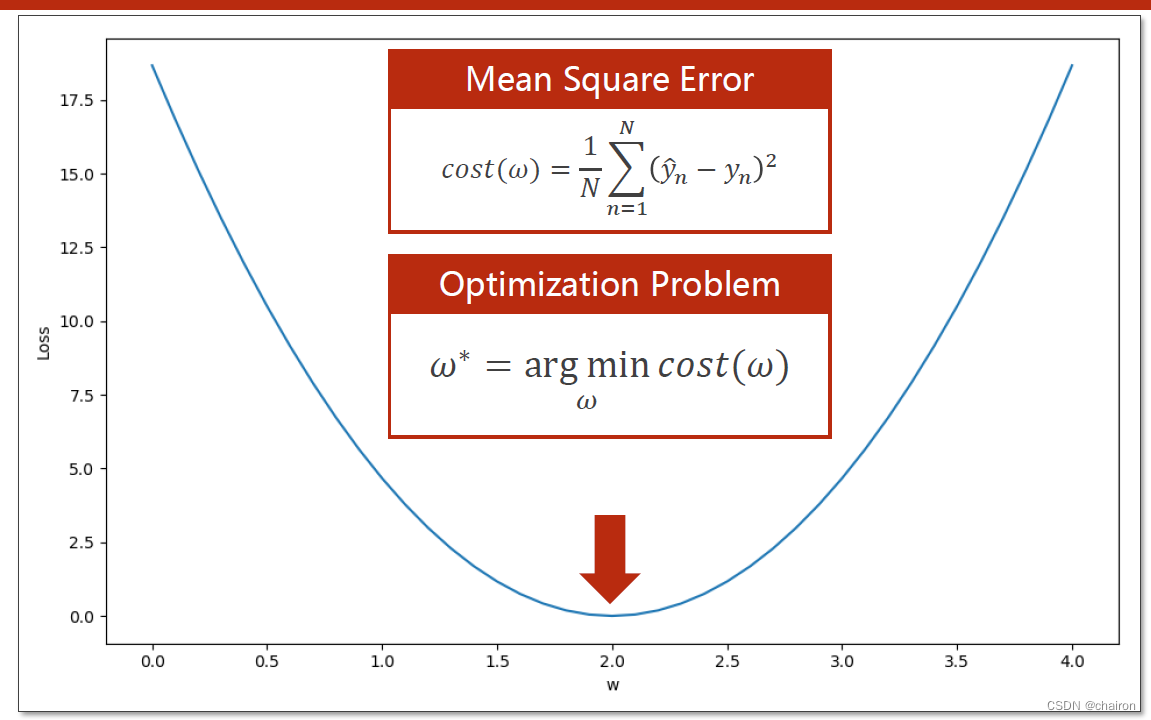
梯度下降算法
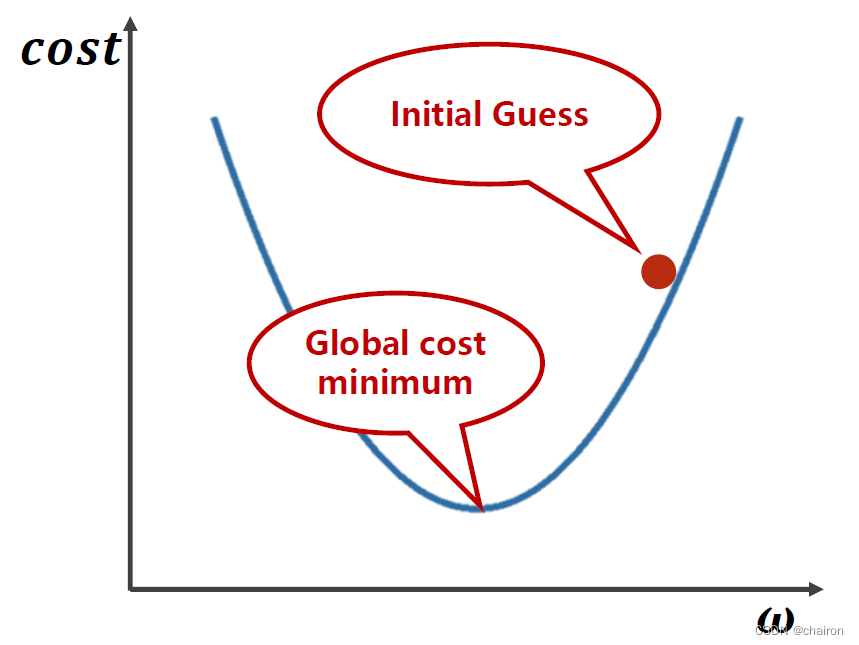
如何才能找到最小的参数w呢?是该往哪个方向走呢?

需要去计算每个点的梯度:即微分(导数),>0:函数上升,损失值在增大,w应该减小(梯度的反方向运动);<0:函数在下降,损失值在减小(目标方向),w应该增大(梯度的反方向运动)。所以参数w的更新方向应该是梯度的负方向!
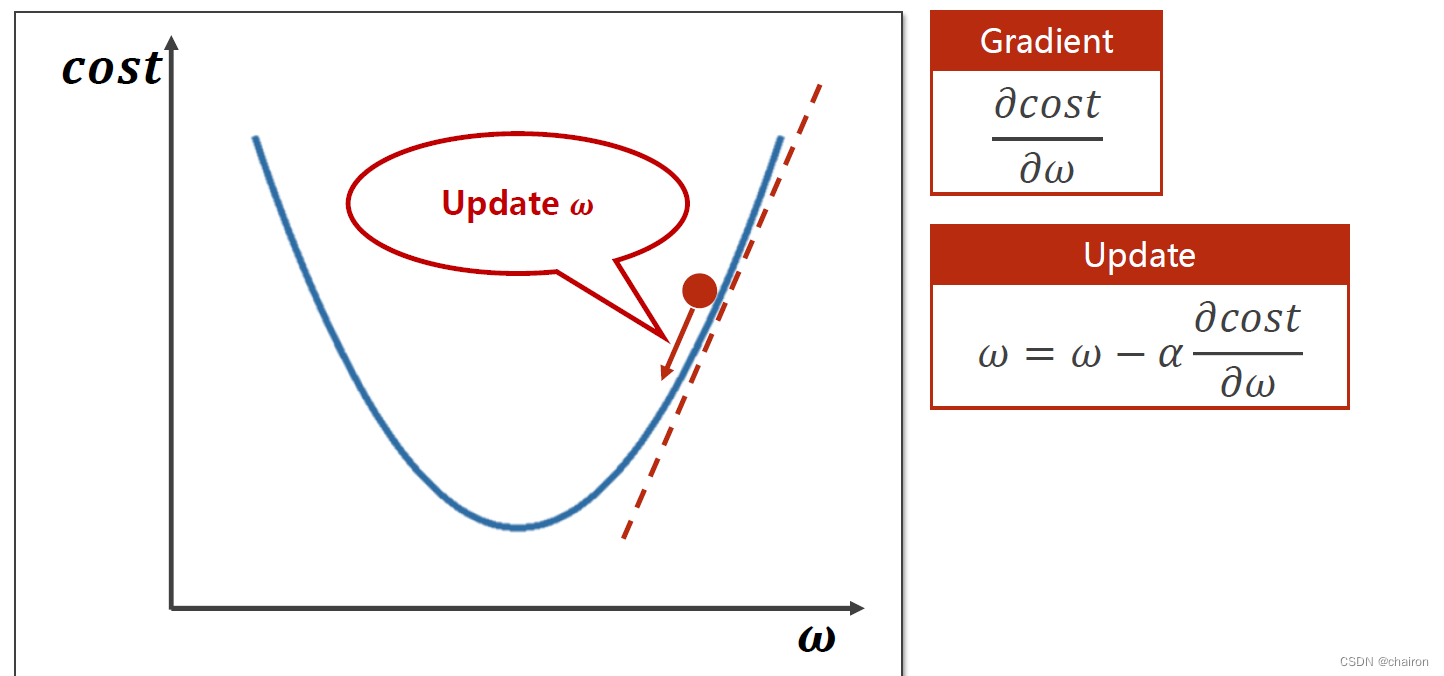
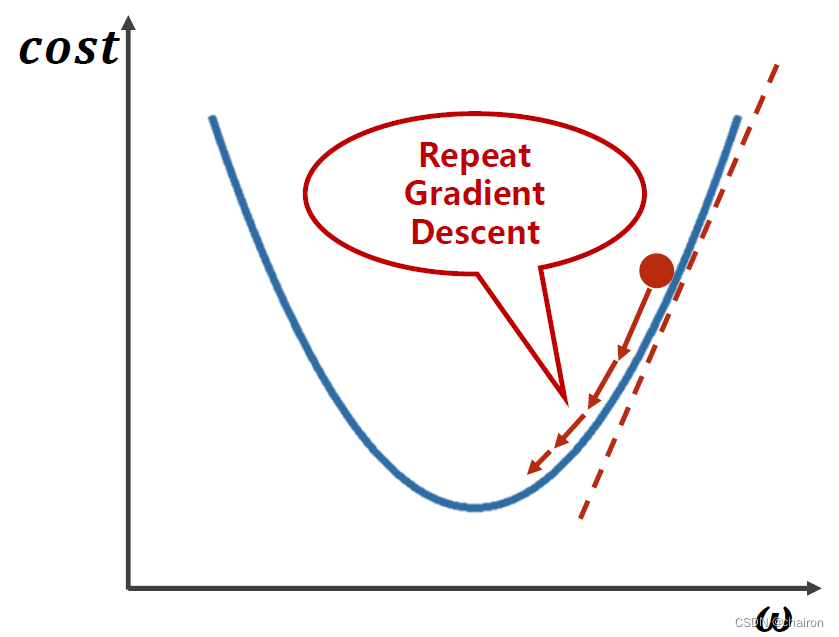
𝛼:学习率。决定你每一步更新走多大步。一般取值很小:0.1、0.01。
注意:梯度下降算法是一种贪心算法,得到的解不一定是全局最优。
解决:
- 运行多次,随机化初始点。(SGD:随机梯度下降)
- 梯度下降法的初始点也是一个超参数。
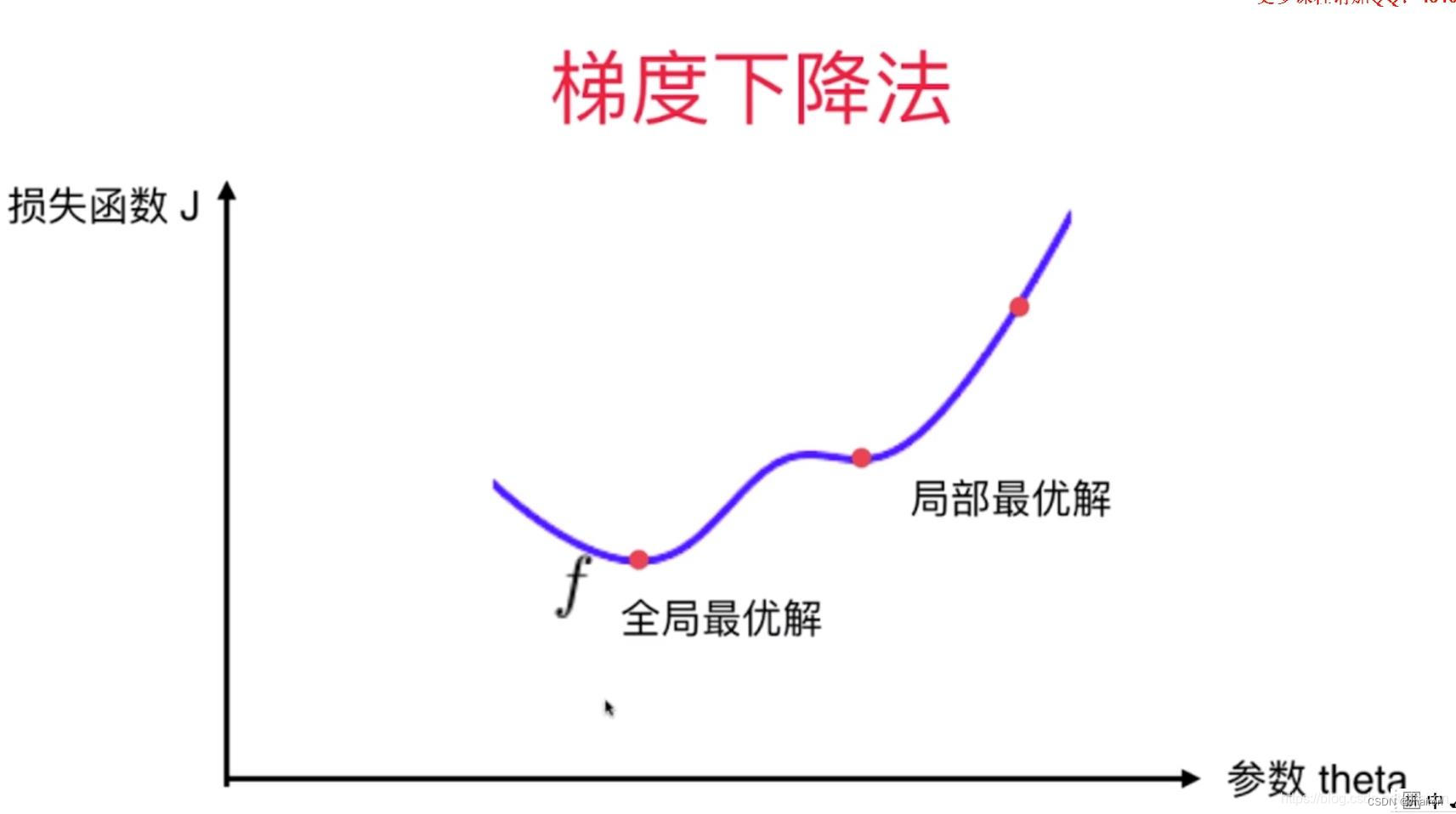
鞍点:梯度为0的点。会导致梯度无法继续更新。
梯度计算
y
n
=
w
?
x
n
y_n=w*x_n
yn?=w?xn?
cost(w)=:
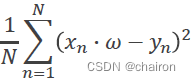

代码
import matplotlib.pyplot as plt
# training set
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 初始化参数
w = 1.0
# 定义线性模型: y = w*x
def forward(x):
return x * w
# 计算 MSE
def cost(xs, ys):
cost = 0
for x, y in zip(xs, ys):
y_pred = forward(x)
cost += (y_pred - y) ** 2
return cost / len(xs)
# 计算梯度
def gradient(xs, ys):
grad = 0
for x, y in zip(xs, ys):
grad += 2 * x * (x * w - y)
return grad / len(xs)
epoch_list = []
cost_list = []
print('predict (before training)', 4, forward(4))
#epoch:训练轮次,表示重复训练的次数
for epoch in range(100):#训练100 epoch
cost_val = cost(x_data, y_data)#计算损失值
grad_val = gradient(x_data, y_data)#计算梯度
w -= 0.01 * grad_val # 更新梯度(参数)0.01 learning rate
print('epoch:', epoch, 'w=', w, 'loss=', cost_val)
epoch_list.append(epoch)
cost_list.append(cost_val)
print('predict (after training)', 4, forward(4))
plt.plot(epoch_list, cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()
epoch: 0 w= 1.0933333333333333 loss= 4.666666666666667
epoch: 1 w= 1.1779555555555554 loss= 3.8362074074074086
epoch: 2 w= 1.2546797037037036 loss= 3.1535329869958857
epoch: 3 w= 1.3242429313580246 loss= 2.592344272332262
epoch: 4 w= 1.3873135910979424 loss= 2.1310222071581117
epoch: 5 w= 1.4444976559288012 loss= 1.7517949663820642
......
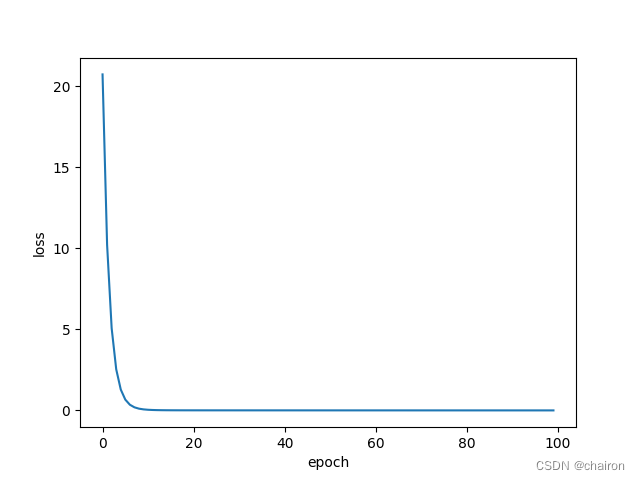
损失曲线图
一般来说,用下图这种epoch、cost(loss)的损失值变化曲线来表示训练情况。
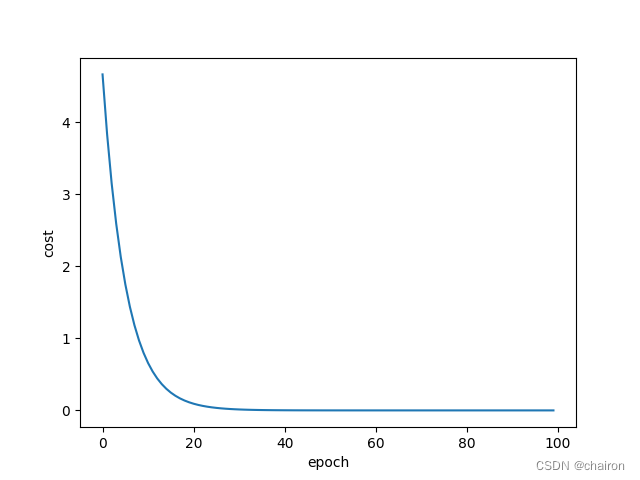
在20 epoch以前,模型快速收敛,后面趋于稳定,损失值接近0.这是理想的训练情况。损失值随着训练越来越小,逐渐收敛,这次训练就是成功的。如果损失值随着训练还逐渐增大了,那么训练就失败了!
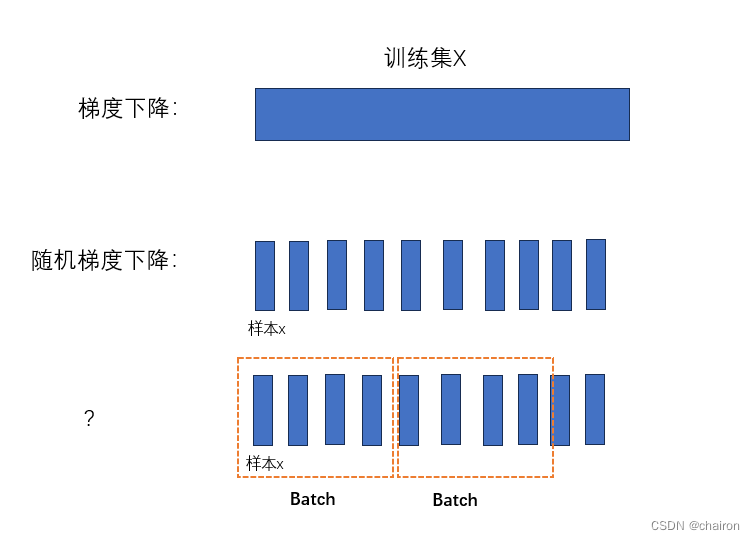
随机梯度下降(Stochastic Gradient Descent)
梯度下降算法:用所有样本的平均损失值cost来更新参数;
随机梯度下降算法:随机选取N个样本中的一个样本的loss来更新参数!
随机梯度下降算法能够更好的解决鞍点问题,因为是随机选取一个样本的loss,可能会跨过鞍点继续更新。

代码
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
def forward(x):
return x * w
# loss function
def loss(x, y):#计算一个样本x的损失值loss
y_pred = forward(x)
return (y_pred - y) ** 2
# 计算梯度 SGD
def gradient(x, y):
return 2 * x * (x * w - y)
epoch_list = []
loss_list = []
print('predict (before training)', 4, forward(4))
for epoch in range(100):
for x, y in zip(x_data, y_data):
grad = gradient(x, y)
w = w - 0.01 * grad # 更新梯度
print("\tgrad:", x, y, grad)
l = loss(x, y)
print("progress:", epoch, "w=", w, "loss=", l)
epoch_list.append(epoch)
loss_list.append(l)
print('predict (after training)', 4, forward(4))
plt.plot(epoch_list, loss_list)
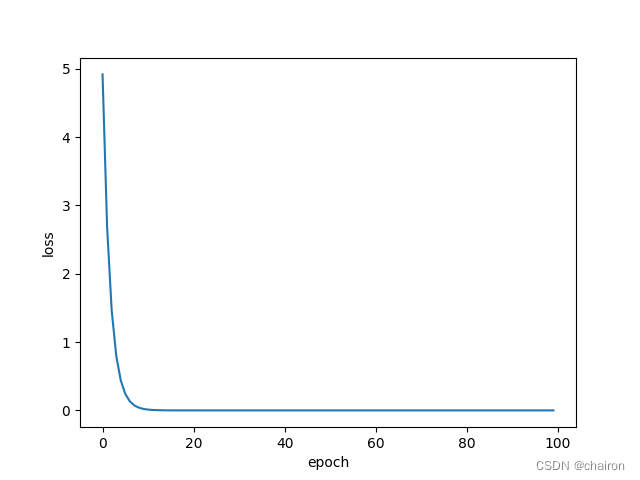
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()
比较
| 梯度下降 | 随机梯度下降 |
|---|---|
| 整个训练集的cost计算梯度 | 一个样本的loss计算梯度 |
| 性能低 | 性能高 |
| 时间复杂度低 | 时间复杂度高 |
有没有一种折中的方法,性能高,时间复杂度又低呢?
采用Batch(Mini-Batch)的方法进行训练。
思考:
这里的线性模型是y=wx,如果换成y=wx+b,上述计算过程会变吗?会影响参数更新吗?
请写出对应的代码。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- PSIM仿真DSP28335ADC功能并使用SCI串口模块输出曲线
- 加速全球普及!移远通信Wi-Fi HaLow模组FGH100M率先通过CE、FCC认证
- 生成式 AI 系统是否需要 GPU?
- Tomcat启动流程分析
- C/C++使用记录
- 哪些行业装配柔性线路板 (FPC)时用到UV胶水?
- 免费SSL证书:为你的网站安全护航
- 基本算法(货仓选址)-排序【竞赛题】
- 高光谱变化检测论文解读分享之基时相差异引导网络的高光谱影像变化检测
- 【实例讲解】通过镜像还原后SSH、JupyterLab无法连接?