力扣日记12.24-【二叉树篇】236. 二叉树的最近公共祖先
发布时间:2023年12月24日
力扣日记:【二叉树篇】236. 二叉树的最近公共祖先
日期:2023.12.24
参考:代码随想录、力扣
ps:提前祝 平安夜快乐!
236. 二叉树的最近公共祖先
题目描述
难度:中等
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
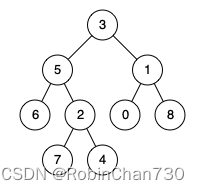
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
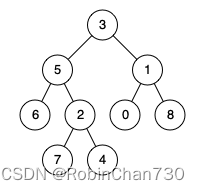
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
- 树中节点数目在范围 [2, 10^5] 内。
- -10^9 <= Node.val <= 10^9
- 所有 Node.val 互不相同 。
- p != q
- p 和 q 均存在于给定的二叉树中。
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
// 本题要找两个子节点的最近公共祖先,是一个从底往上找的过程(先找到子节点才能找其祖先)
// 而要从底往上查找->想到是回溯->想到二叉树遍历中的天然回溯,即后序遍历(左右中,根据左右节点的返回值处理中节点逻辑)
// 且从底往上找,则先找到的公共祖先一定是最近公共祖先(深度最大)
// 关于如何判断一个节点是节点q和节点p的公共祖先:
// 第一种情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者反之,那么该节点就是节点p和q的最近公共祖先
// 第二种情况:节点本身p(q),是自己的祖先(实际上在代码实现中也包含在第一种情况中)
// 递归参数与返回值:参数为当前节点与指定节点;返回值表示是否在当前节点的树中找到指定节点(或者找到公共祖先)
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// 递归终止条件
// 如果root为空节点了,则没有,返回空
// 如果 root == q,或者 root == p,说明找到 q p ,则将其返回
if (root == q || root == p || root == NULL) return root;
// 如果根节点不为空或还没找到,则递归处理
// 左(看左子树能不能找到p或q)
TreeNode* left = lowestCommonAncestor(root->left, p, q);
// 右(看右子树能不能找到p或q)
TreeNode* right = lowestCommonAncestor(root->right, p, q);
// 中(对左右返回值的处理逻辑)
// 如果左右不为空,说明左子树返回一个,右子树返回一个,则当前root为公共祖先(情况1)
if (left != NULL && right != NULL) return root;
// 如果左为空而右不为空,说明右找到了一个或者直接找到公共祖先,返回右(包含了情况2)
if (left == NULL && right != NULL) return right;
// 反之亦然
if (left != NULL && right == NULL) return left;
// 如果都为空,则返回空
return NULL;
}
};
复杂度
时间复杂度:
空间复杂度:
思路总结
-
本题想了想没有思路www直接看的代码随想录的…
-
首先明确祖先的概念:一个节点,是 以该节点为根节点的树上的所有节点的祖先;关于最近公共祖先的概念则为题目所述
-
本题思路(实际上是代码注释):
- 本题要找两个子节点的最近公共祖先,是一个从底往上找的过程(先找到子节点才能找其祖先)
- 而要从底往上查找->想到是回溯->想到二叉树遍历中的天然回溯,即后序遍历(左右中,根据左右节点的返回值处理中节点逻辑)
- 且从底往上找,则先找到的公共祖先一定是最近公共祖先(深度最大)
- 关于如何判断一个节点是节点q和节点p的公共祖先:
- 第一种情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者反之,那么该节点就是节点p和q的最近公共祖先
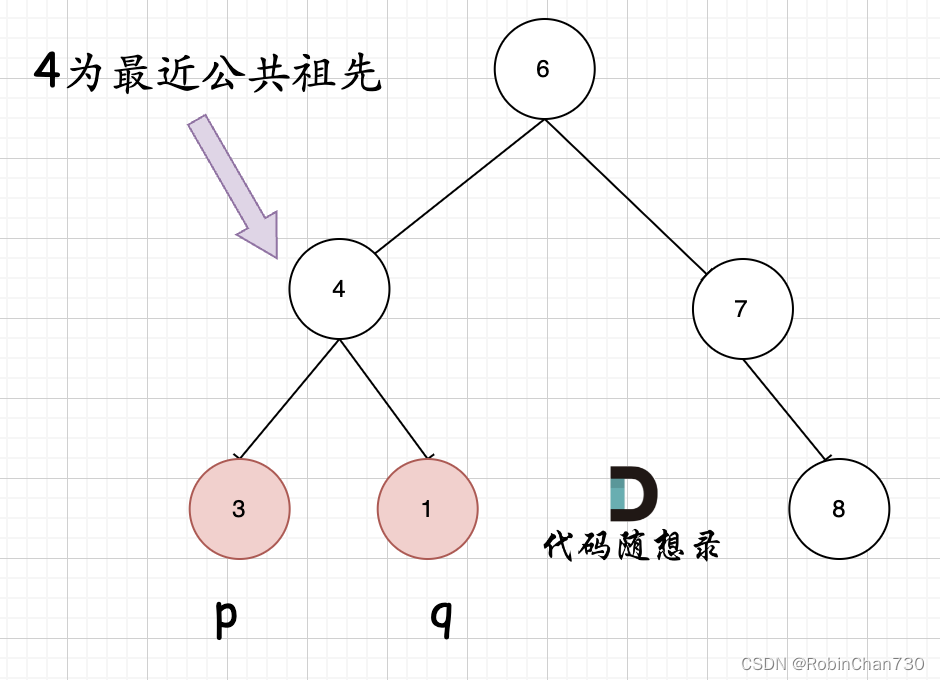
- 第二种情况:节点本身p(q),是自己的祖先(实际上在代码实现中也包含在第一种情况中)
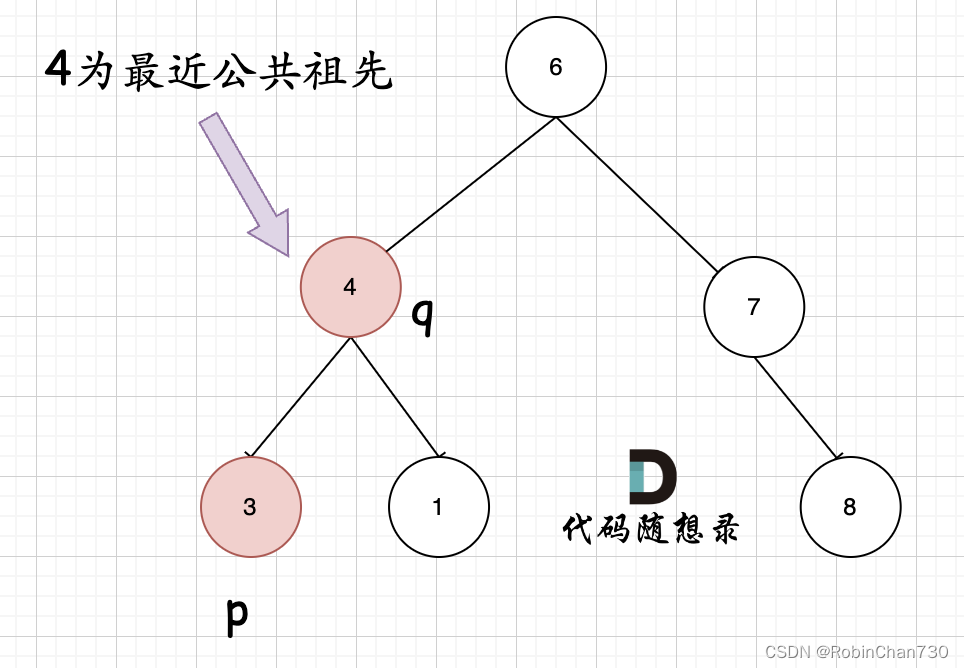
- 第一种情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者反之,那么该节点就是节点p和q的最近公共祖先
- 递归的三部曲:
- 递归参数与返回值:参数为当前节点与指定节点;返回值表示是否在当前节点的树中找到指定节点(或者找到公共祖先)
- 递归终止条件:
- 如果root为空节点了,则没有,返回空
- 如果
root == q,或者root == p,说明找到 q p ,则将其返回
- 递归处理逻辑:
- 如果根节点不为空或还没找到,则递归处理
- 左(看左子树能不能找到p或q)
- 右(看右子树能不能找到p或q)
- 中(对左右返回值的处理逻辑)
- 如果左右不为空,说明左子树返回一个,右子树返回一个,则当前root为公共祖先;(对应情况1)
- 如果左为空而右不为空,说明右找到了一个或者直接找到公共祖先,返回右(反之亦然)(包含了情况2,当然也对情况1的处理也可能有此步骤)
- 如果都为空,则返回空。
-
mark:之后再仔细看看 代码随想录中 关于返回值的描述。
在递归函数有返回值的情况下:如果要搜索一条边,递归函数返回值不为空的时候,立刻返回,如果搜索整个树,直接用一个变量left、right接住返回值,这个left、right后序还有逻辑处理的需要,也就是后序遍历中处理中间节点的逻辑(也是回溯)。
且代码随想录对本题的解析也很清晰,可以再读读。
-
寻找最小公共祖先完整流程图如下:
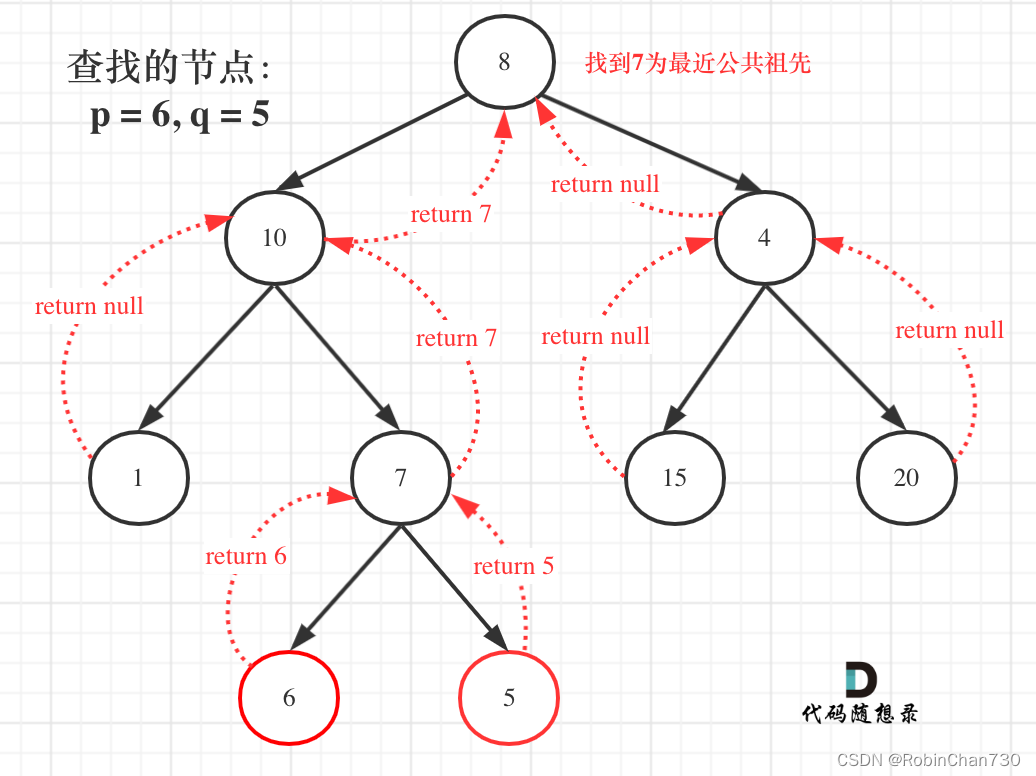
文章来源:https://blog.csdn.net/weixin_45847708/article/details/135179957
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JavaSec基础 反射修改Final修饰的属性及绕过高版本反射限制
- 【建议收藏】一文全面解读Linux最常用的解压缩命令(tar、zip、unzip、gzip、guznip、bzip2、bunzip2)
- 【面试高频算法解析】算法练习2 回溯
- 计算机网络第三章(谢希仁)
- c语言的练习---BCD解密
- 什么是消费增值,我来简单说说
- 如何解决idea创建版本时只有Java21和Java17选项
- AntDB内存管理之内存上下文之如何使用内存上下文
- 高级编程。JavaScript中有哪些类型转换机制?
- Linux中关于rpm管理包命令详解