计算机组成原理之原/反/补码和定点小数

学习的最大理由是想摆脱平庸，早一天就多一份人生的精彩；迟一天就多一天平庸的困扰。各位小伙伴，如果您：
想系统/深入学习某技术知识点…
一个人摸索学习很难坚持，想组团高效学习…
想写博客但无从下手，急需写作干货注入能量…
热爱写作，愿意让自己成为更好的人…

---

前言

一、带符号整数表示和运算（原/反/补码）
1、原码
2、原码、补码快速转换
3、补码的加法运算
4、补码的减法运算
二、原/反/补码的对比
三、移码
四、定点小数表示和运算
1、定点小数的加/减运算
2、定点小数与定点整数对比
3、小数补码的加法运算
4、小数补码的减法运算

---

一、带符号整数表示和运算（原/反/补码）

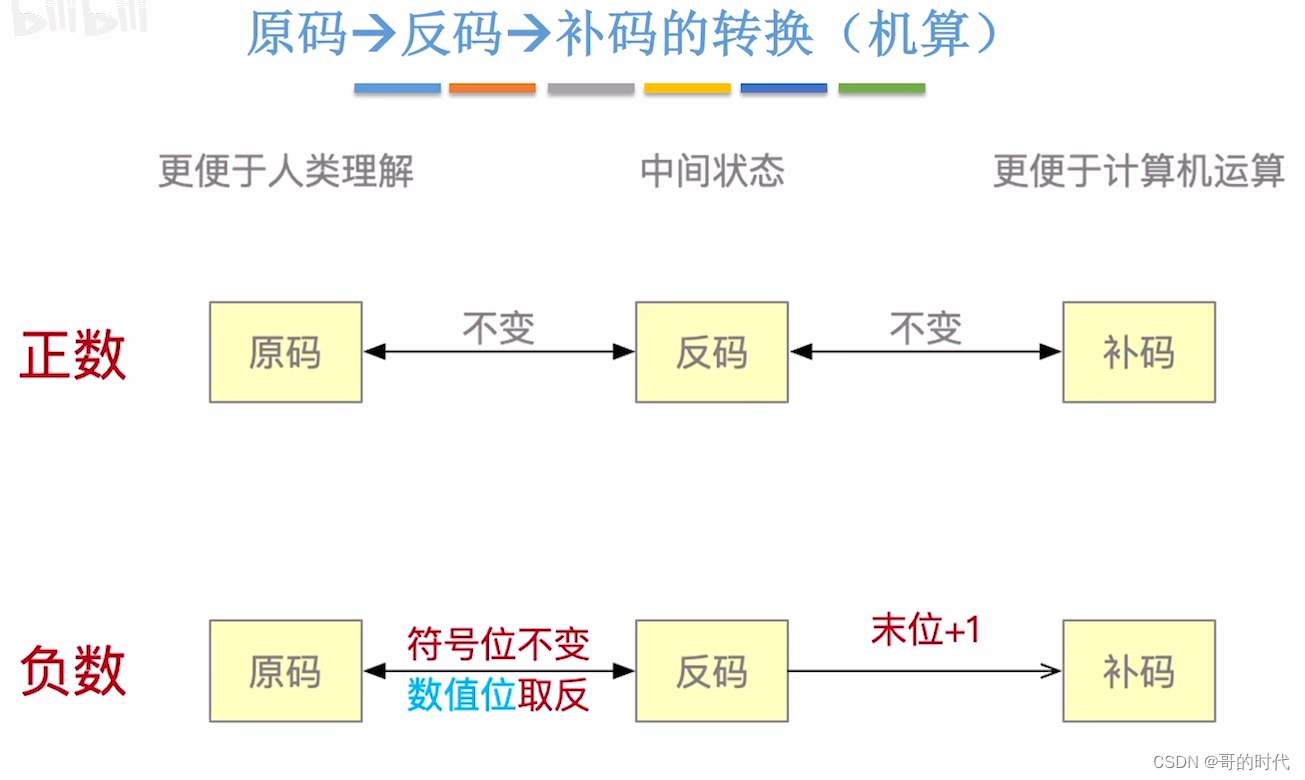
1、原码

• 符号位“0/1”对应“正/负”，剩余的数值位表示真值的绝对值
• 若机器字长n+1位，带符号整数的原码表示范围: 一(2^n—1) ≤x ≤2^n—1
• 真值0有两种形式:+0 和-0 ，[+0]原=0,0000000;[-0]原=1,0000000

缺点：
符号位不能参与运算，需要设计复杂的硬件电路才能处理，费钱!贵!

2、原码、补码快速转换

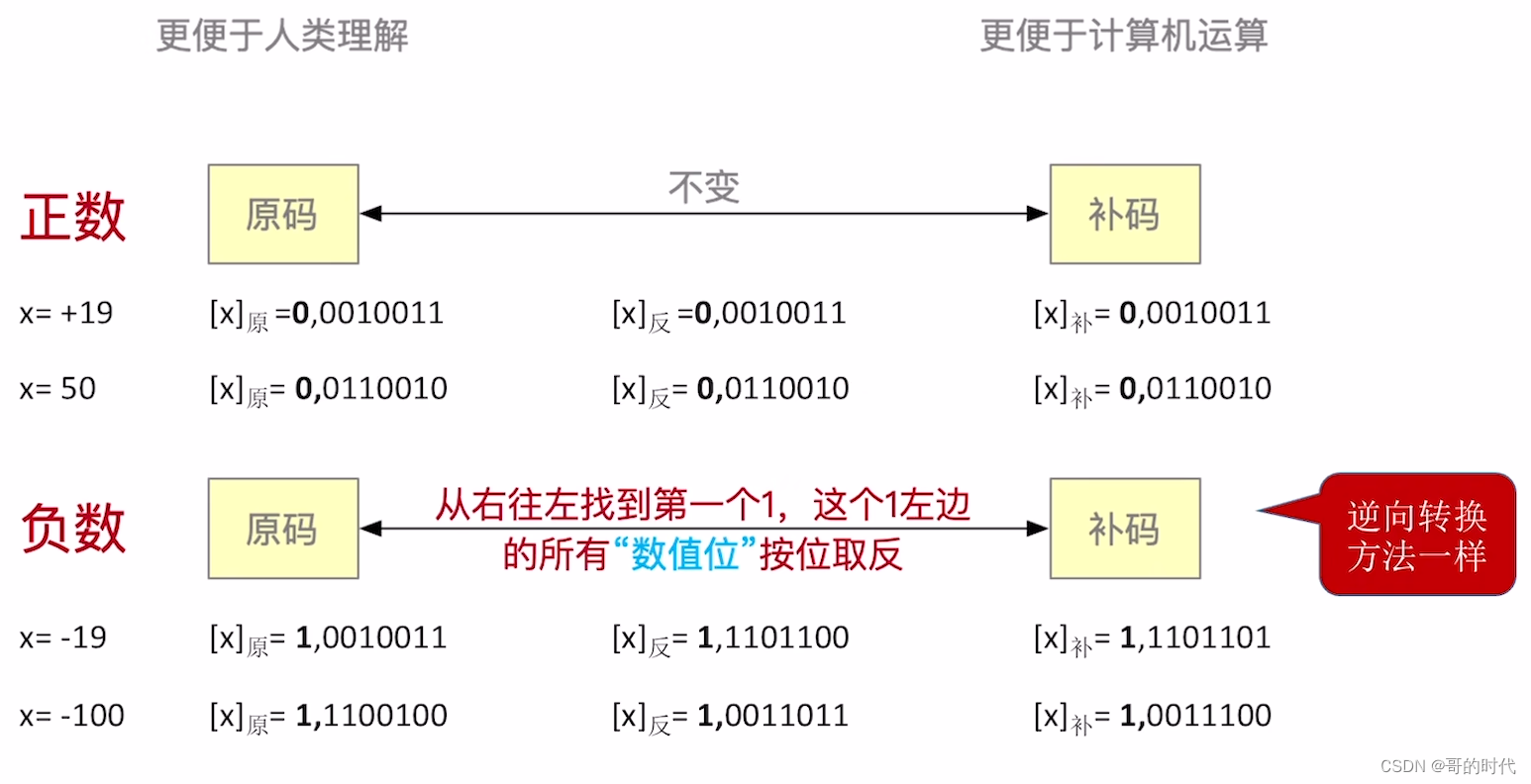
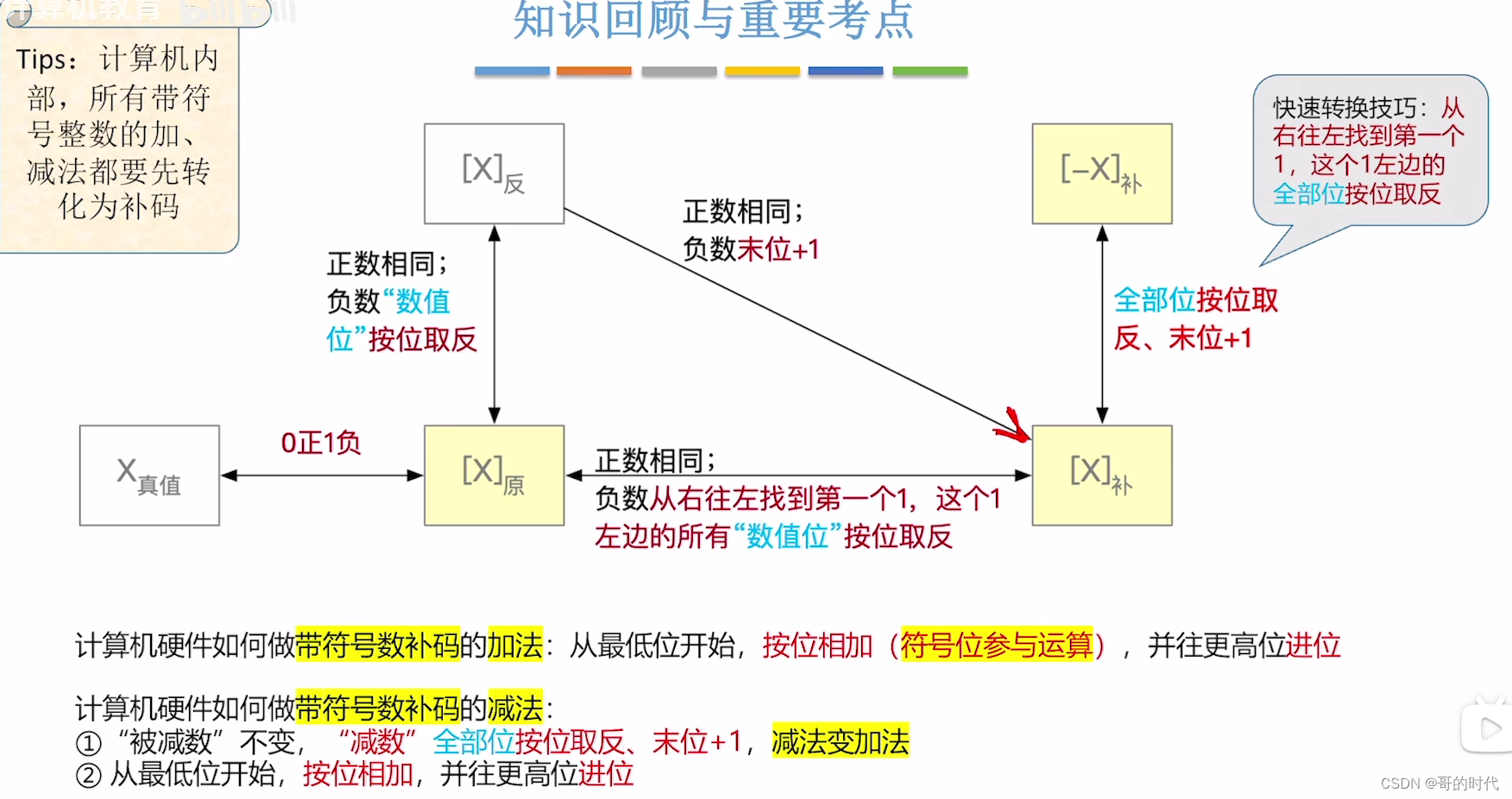
3、补码的加法运算

从最低位开始，按位相加（符号位参与运算），并往更高位进位

例1

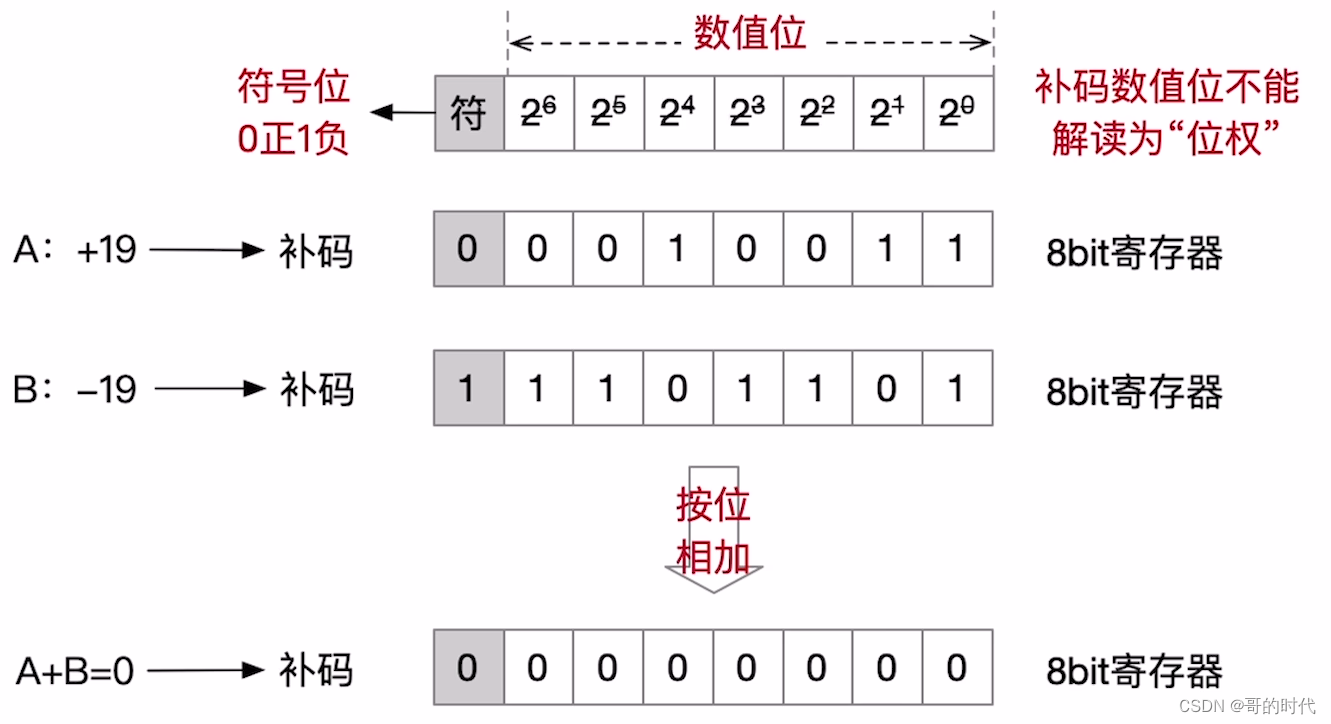
例2

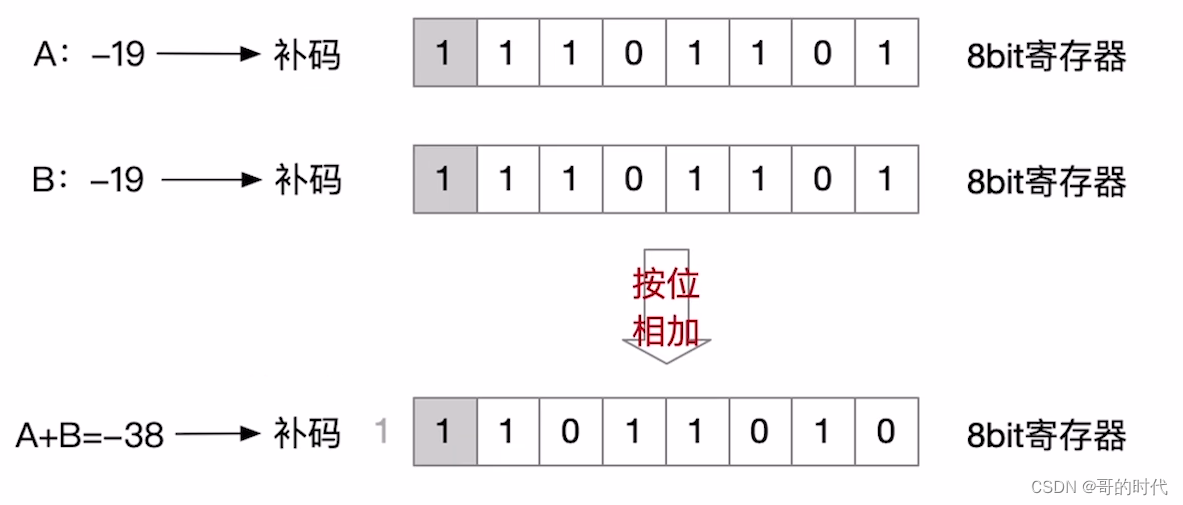
4、补码的减法运算

将减法变成加法


例题

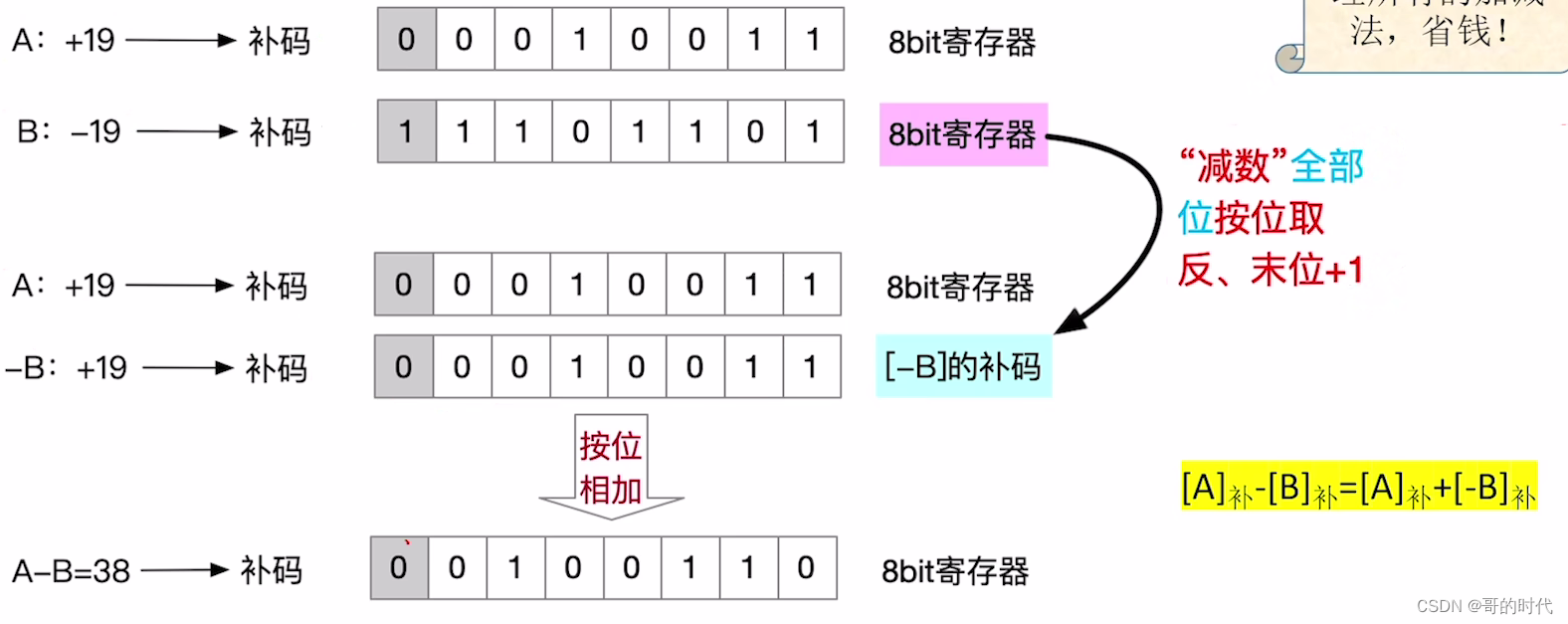
重点：

二、原/反/补码的对比

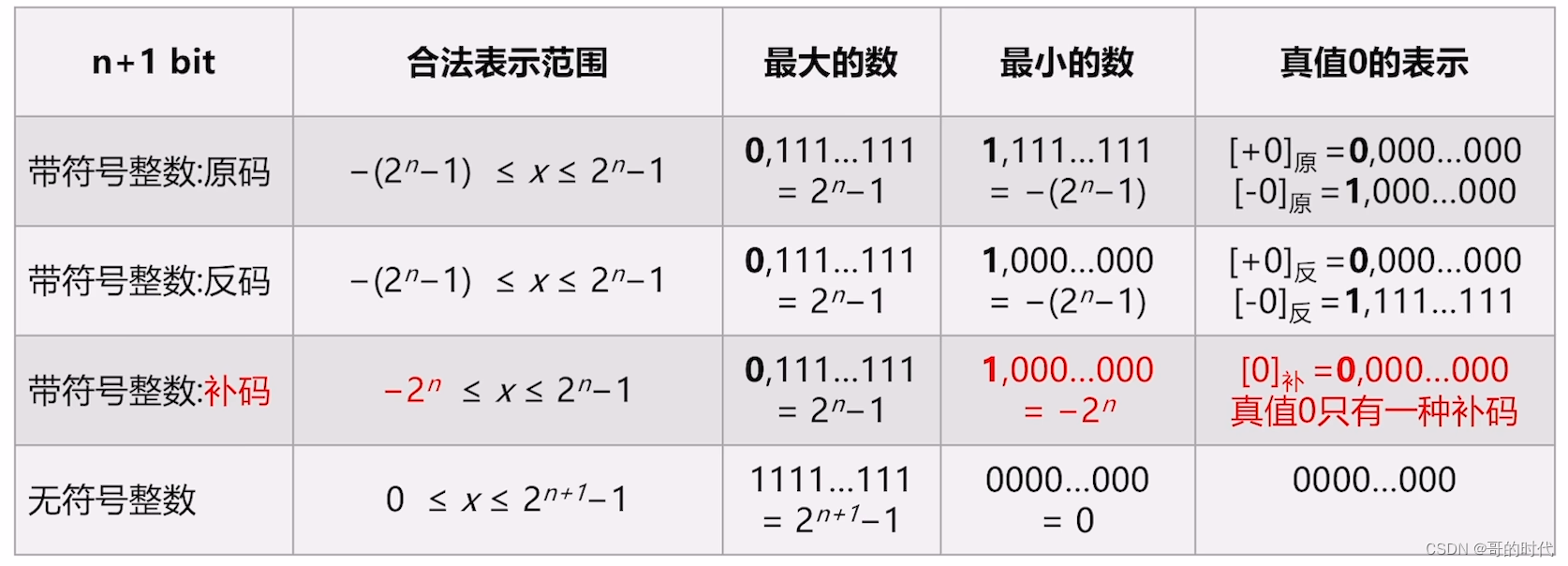
• 原码和反码的合法表示范围完全相同，都有两种方法表示真值0
• 补码的合法表示范围比原码多一个负数，只有一种方法表示真值0
  
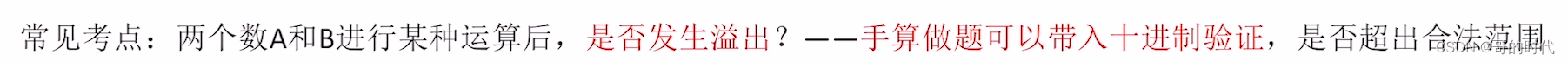
  例如：A（-64）+B（-64）=-128，原码对于8bit而言取值范围为：-127_{127，所以算溢出。补码对于8bit而言取值范围为：-128}127,所以不算溢出。

三、移码

移码:补码的基础上将符号位取反。注意:移码只能用于表示整数


若机器字长n+1位，移码整数的表示范围:一2^n ≤x≤2^n一1（与补码相同）

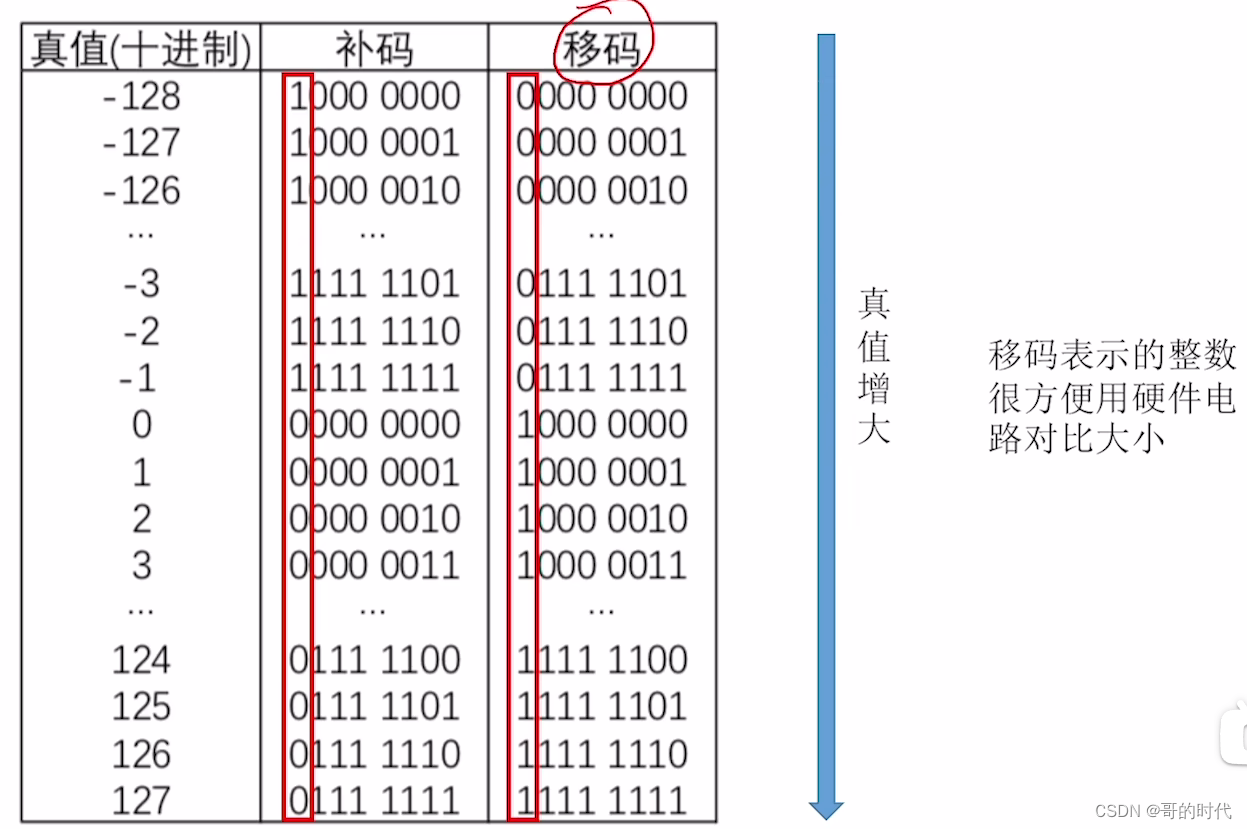
总结：

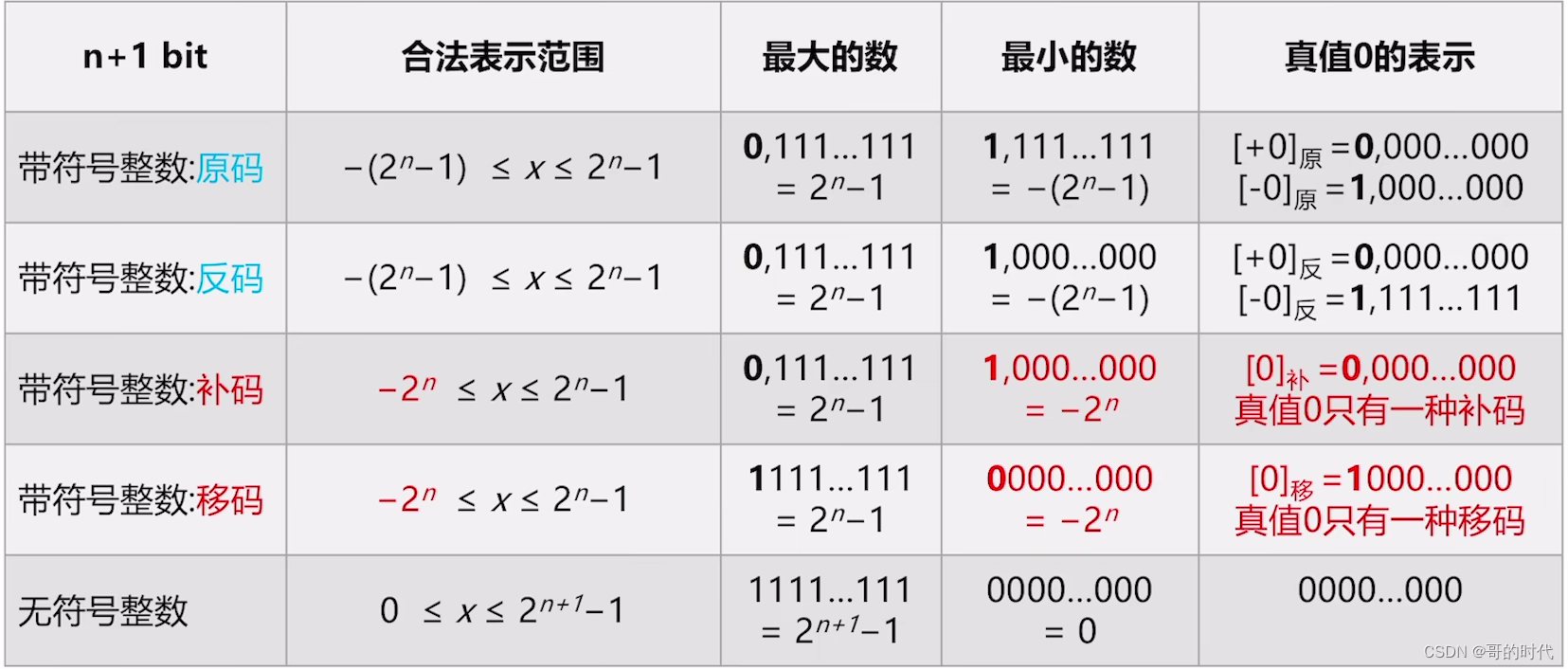
• 原码和反码的合法表示范围完全相同，都有两种方法表示真值0
• 补码的合法表示范围比原码多一个负数，只有一种方法表示真值0
• 移码的合法表示范围比原码多一个负数，只有一种方法表示真值0
  
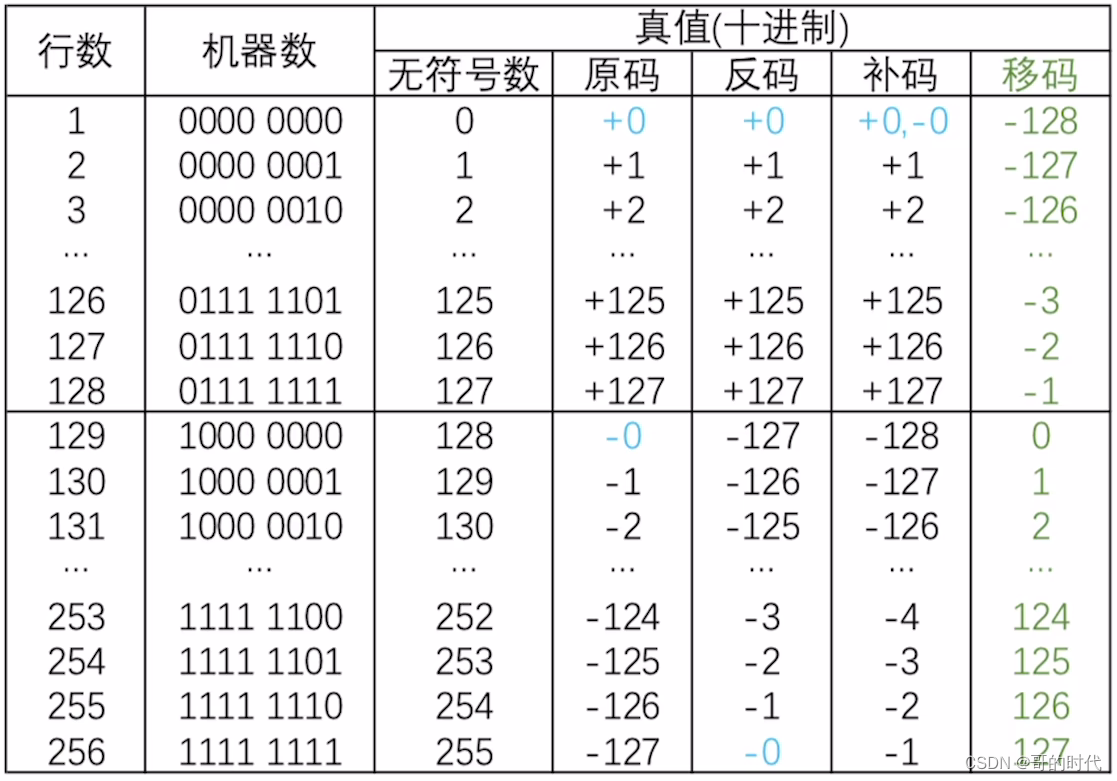
• 原码和反码的真值0有两种表示
• 补码和移码的真值0只有一种表示
• 补码和移码可以多表示一个负数

例题：

四、定点小数表示和运算

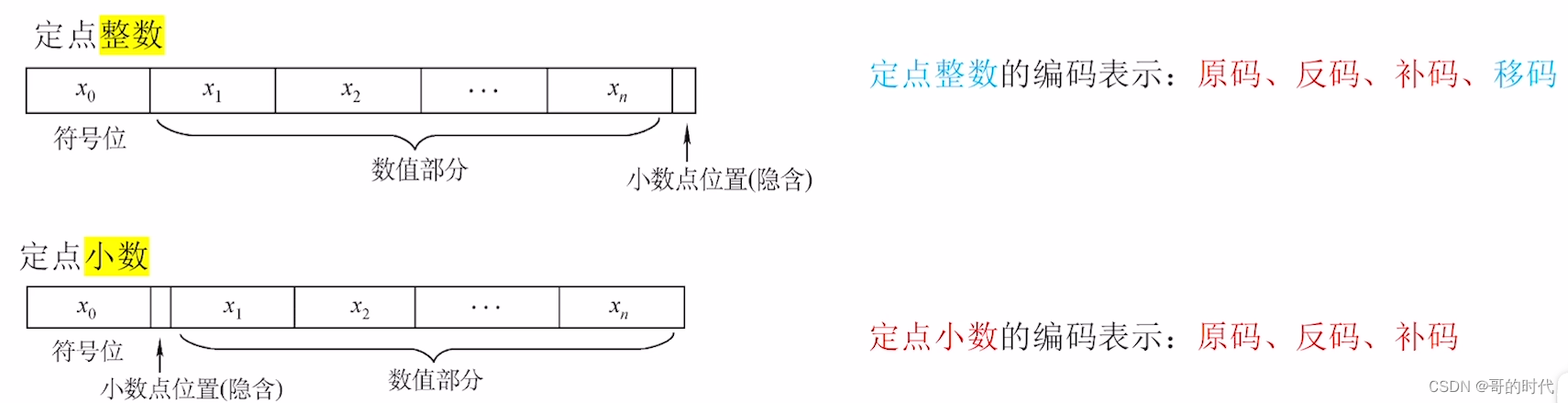
1、定点小数的加/减运算

对两个定点小数A、B进行加法/减法时，需要先转换为补码

计算机硬件如何做定点小数补码的加法:从最低位开始，按位相加(符号位参与运算)，并往更高位进位

计算机硬件如何做定点小数补码的减法:

• “被减数”不变，“咸数”全部位按位取反、末位+1，减法变加法
• 从最低位开始，按位相加，并往更高位进位

2、定点小数与定点整数对比

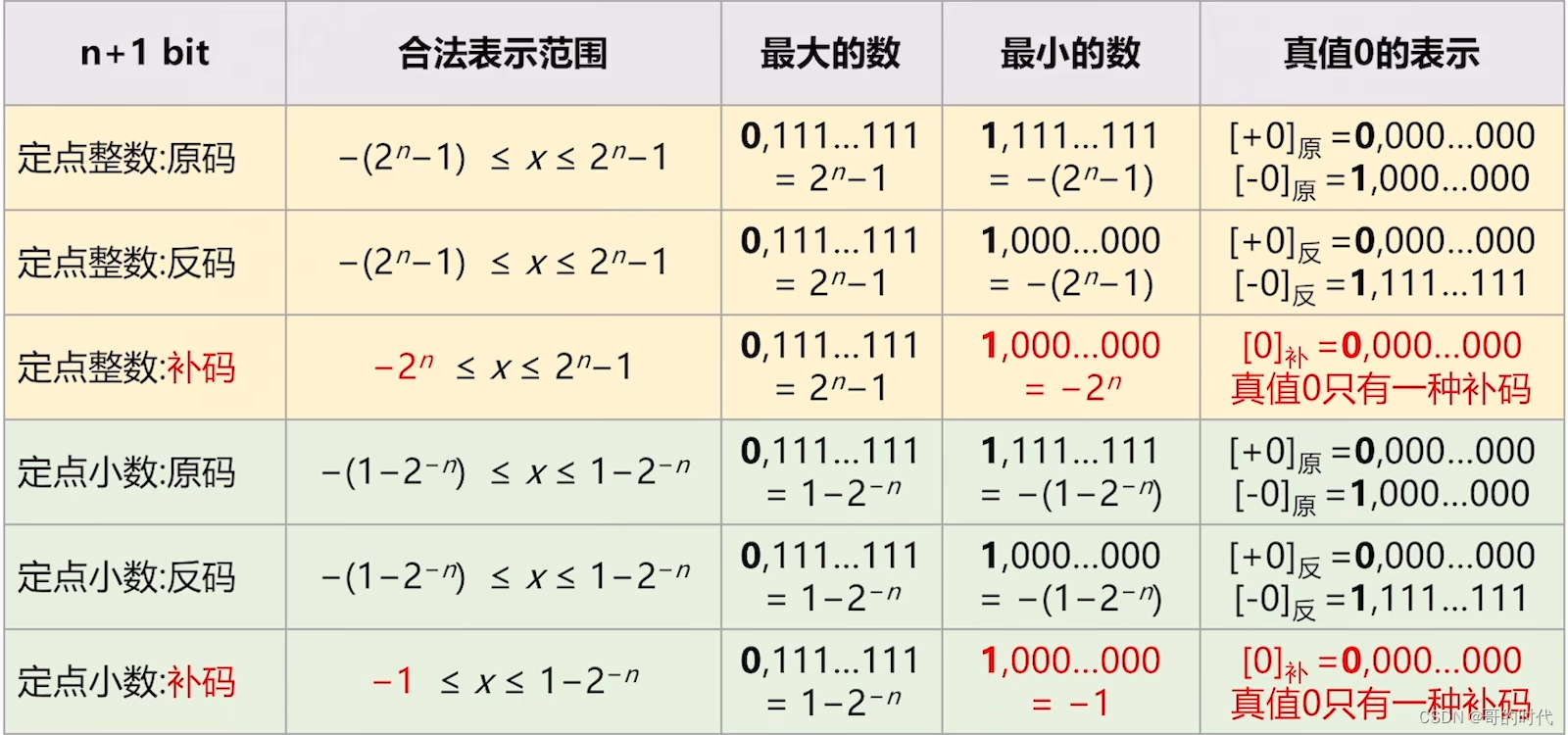
3、小数补码的加法运算

计算机硬件如何做补码的加法:从最低位开始，按位相加（符号位参与运算），并往更高位进位

例1（整数）

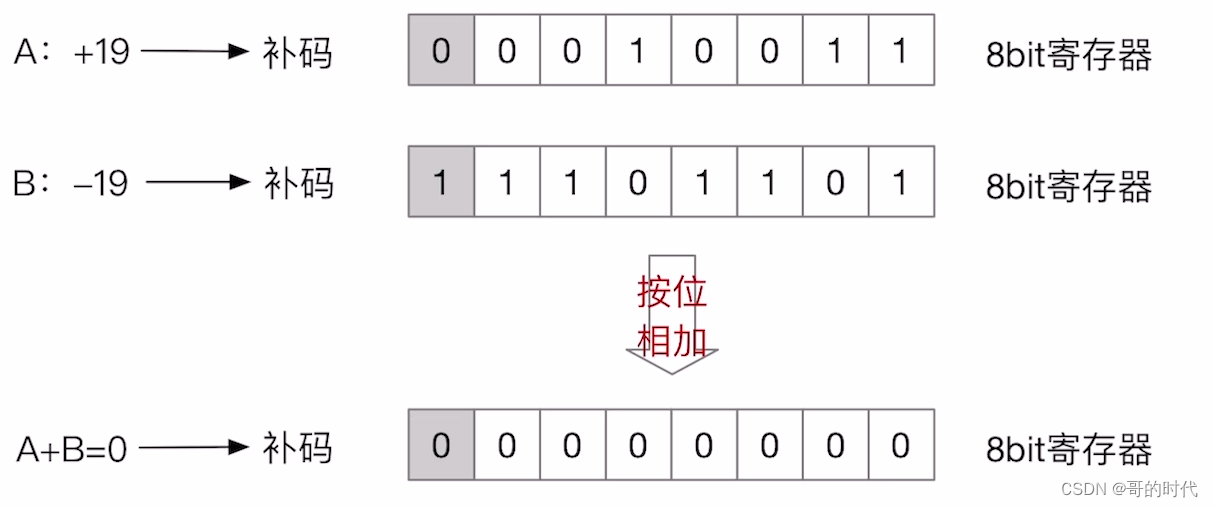
例2（小数）

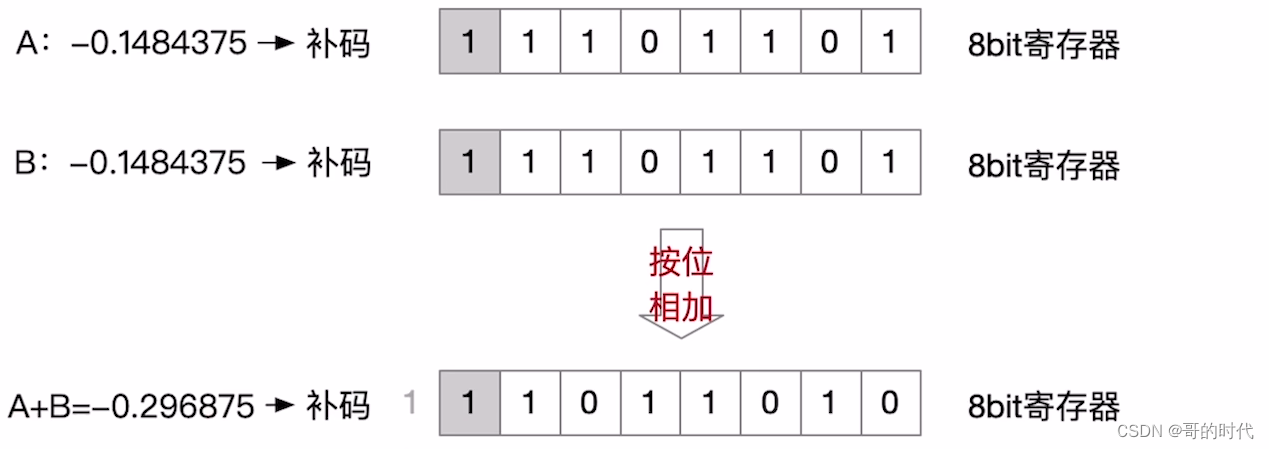
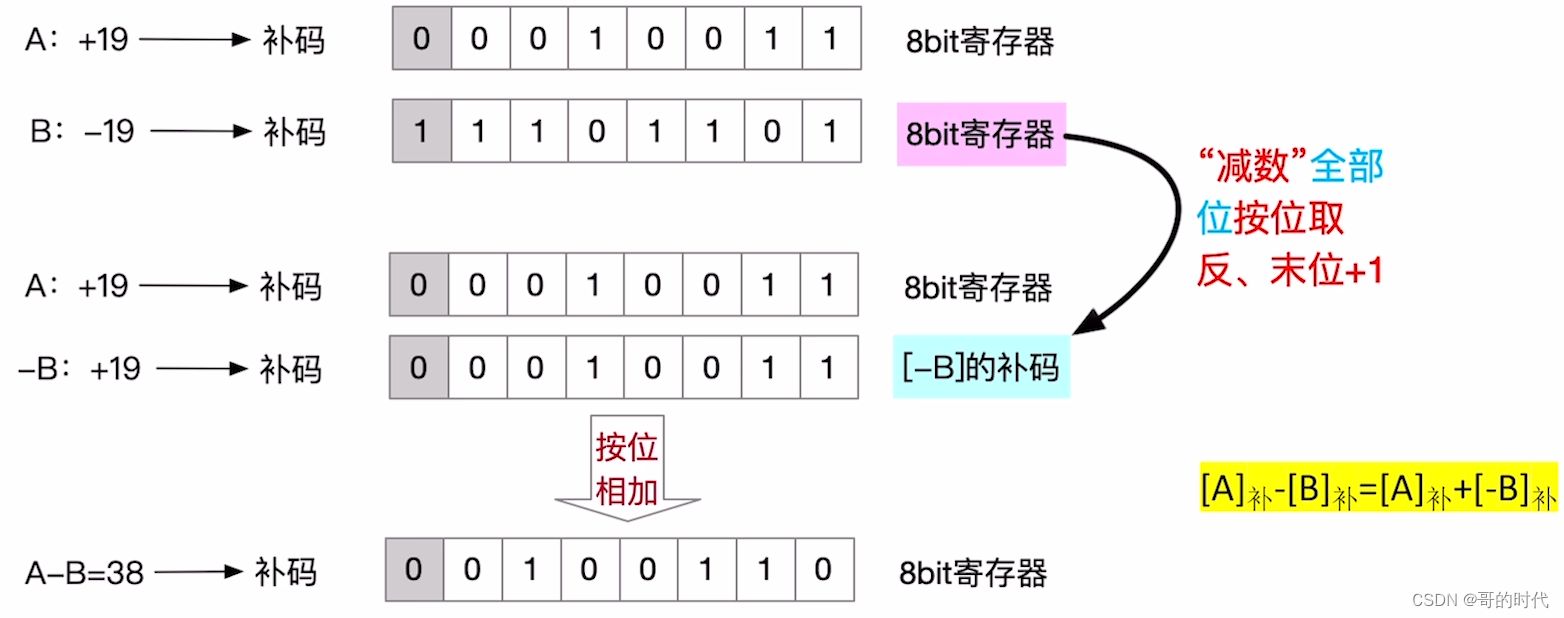
4、小数补码的减法运算

计算机硬件如何做带符号数补码的减法:

• “被减数”不变，“减数”全部位按位取反、末位+1，减法变加法
• 从最低位开始，按位相加，并往更高位进位

例1

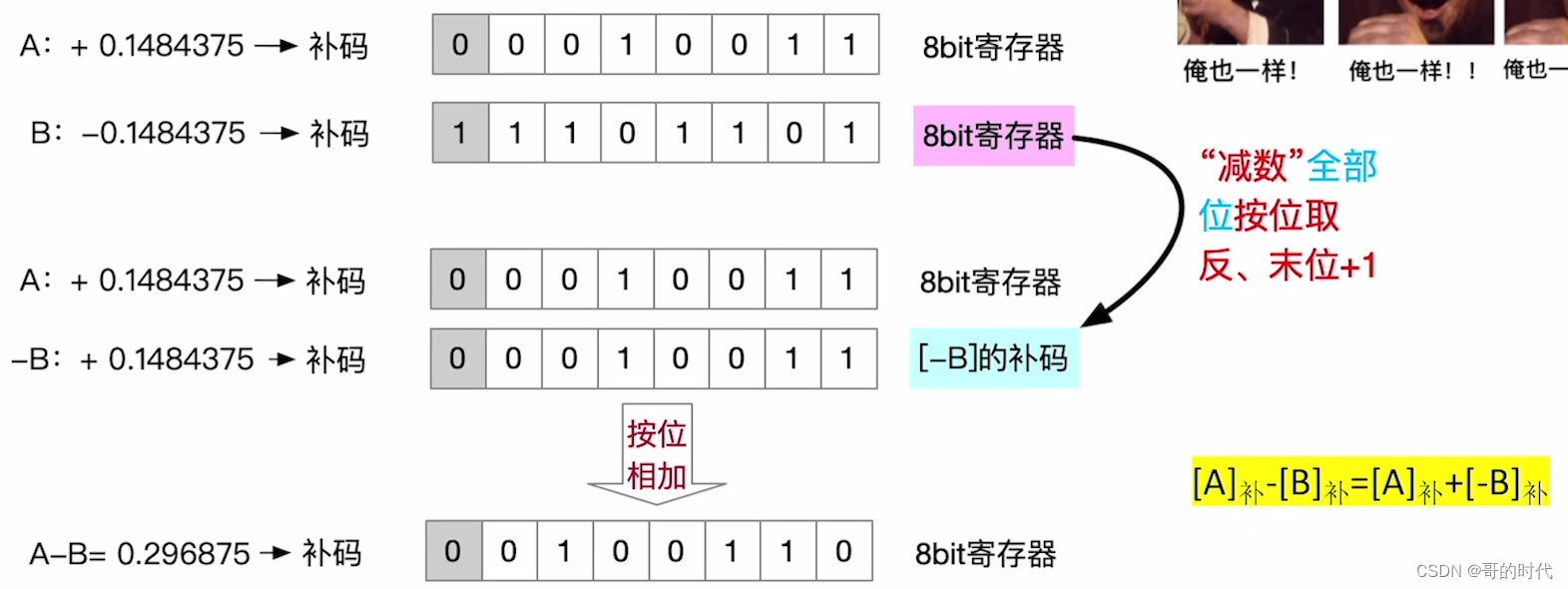
例2

---

总结

以上就是计算机组成原理之原/反/补码和定点小数的相关知识点，希望对你有所帮助。
积跬步以至千里，积怠惰以至深渊。时代在这跟着你一起努力哦！