代码随想录算法训练营第四天| 24. 两两交换链表中的节点、19.删除链表的倒数第N个节点面试题 02.07. 链表相交、142.环形链表II
文档讲解:虚拟头节点,三指针,快慢指针,链表相交,环形链表,
技巧:
1、对于指针的操作要画图,明确步骤后好做了
2、使用虚拟头节点可以避免对头节点单独讨论,且方便对头节点操作
24. 两两交换链表中的节点
两两交换需要使用三指针分别指向连续链接的节点,在前两节点交换时不会丢失第三节点(指针操作复杂,要明确每一步操作)
使用虚拟头节点可以避免对头节点单独讨论
三指针:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode * dummyNode = new ListNode(0);
dummyNode->next = head;
ListNode * left = dummyNode;
ListNode * cur = dummyNode->next;
ListNode * right;
while(cur != nullptr){
right = cur->next;
if(right == nullptr) break;
cur->next = right->next;
right->next = cur;
left->next = right;
left = cur;
cur = cur->next;
}
return dummyNode->next;
}
};
19.删除链表的倒数第N个节点
定义fast指针和slow指针,初始值为虚拟头结点
fast首先走n + 1步 ,同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作)
快慢指针
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode * dummyNode = new ListNode(0);
dummyNode->next = head;
ListNode * slow = dummyNode, * fast = dummyNode;
int i = 0;
while(i <= n){
if(fast == nullptr) return nullptr;
fast = fast->next;
i++;
}
ListNode * temp = slow;
slow = slow->next;//slow为头节点,fast指向第n+1个节点
while(fast != nullptr){
fast = fast->next;
temp = slow;
slow = slow->next;
}
temp->next = slow->next;//可能删除head
delete slow;
return dummyNode->next;//因为head可能被删除,但dummy的next会指向新head
}
};
面试题 02.07. 链表相交
求出两个链表长度的差值L;
然后根据差值将两链表的遍历指针的起始位置对齐,即较长链表的指针需先走L步;
若存在交点,则必为第一次两指针相同的位置(注意不是元素值相同处)
快慢指针
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0, lenB = 0;
ListNode * NodeA = headA, *NodeB = headB;
while(NodeA != nullptr || NodeB != nullptr){
if(NodeA != nullptr){
lenA++;
NodeA = NodeA->next;
}
if(NodeB != nullptr){
lenB++;
NodeB = NodeB->next;
}
}
int len = lenA > lenB? lenA-lenB:lenB-lenA;
if(lenA - lenB > 0){
NodeA = headA;
NodeB = headB;
}
else{
NodeA = headB;//NodeA一定指向较长链表的头节点
NodeB = headA;
}
for(int i = 0; i < len; i++){
NodeA = NodeA->next;
}
while(NodeA != nullptr){
if(NodeA == NodeB) return NodeA;
NodeA = NodeA->next;
NodeB = NodeB->next;
}
return nullptr;
}
};
142.环形链表II
1、使用两个指针,fast和low指针遍历链表,fast每次前进两步,low每次前进一步。
2、第一次相遇后,将两指针分别从head和相遇点同时前进,每次前进一步,则必相交于环入口。{原因:x = (n -1)(y + z) + z}
已经确定有环时,如何确定环入口:
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点再到环形入口节点节点数为 z。 如图所示:
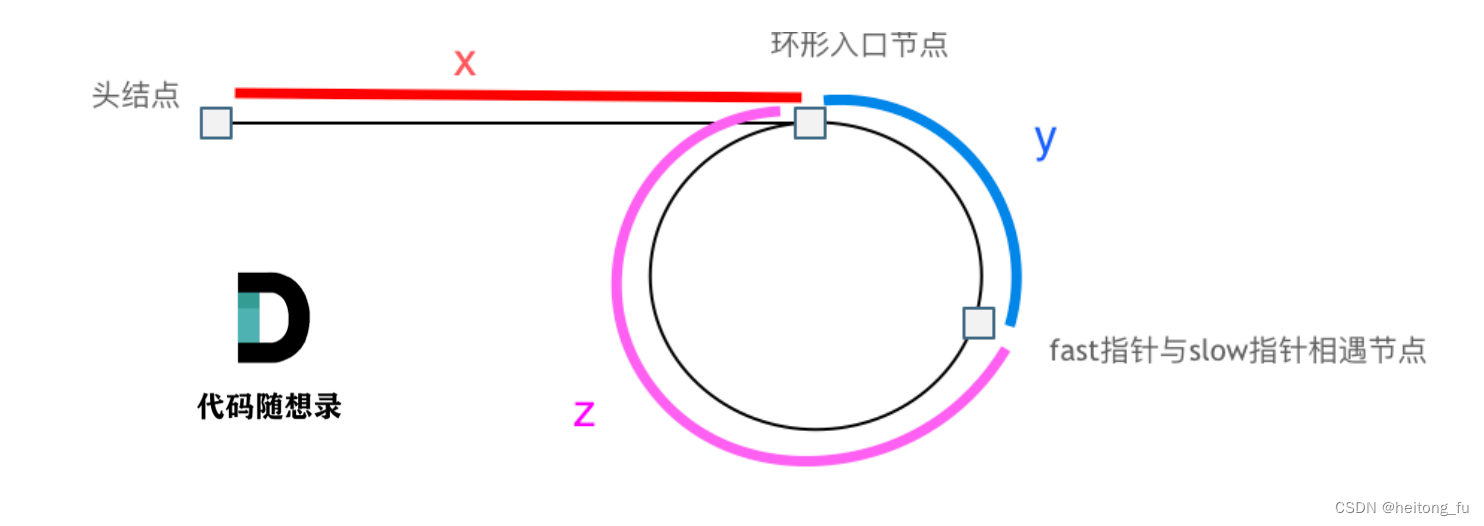
那么相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈环内节点的个数。
因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2:(x + y) * 2 = x + y + n (y + z)
因为要找环形的入口,那么要求的是x,因为x表示 头结点到 环形入口节点的的距离。
整理得:x = (n -1)(y + z) + z 表示从头结点出发一个指针node1,从相遇节点也出发一个指针node2,步进均为1,node1走x到环入口时,node2走n-1圈环后又z正好也走到环入口。
注意:n一定是大于等于1的,因为 fast指针至少要多走一圈才能相遇slow指针
快慢指针
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode * slow = head, * fast = head;
while(fast != nullptr && fast->next != nullptr){
fast = fast->next->next;
slow = slow->next;
if(slow == fast) {
slow = head;
while(slow != fast){
slow = slow->next;
fast = fast->next;
}
return slow;
}
}
return nullptr;
}
};
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!