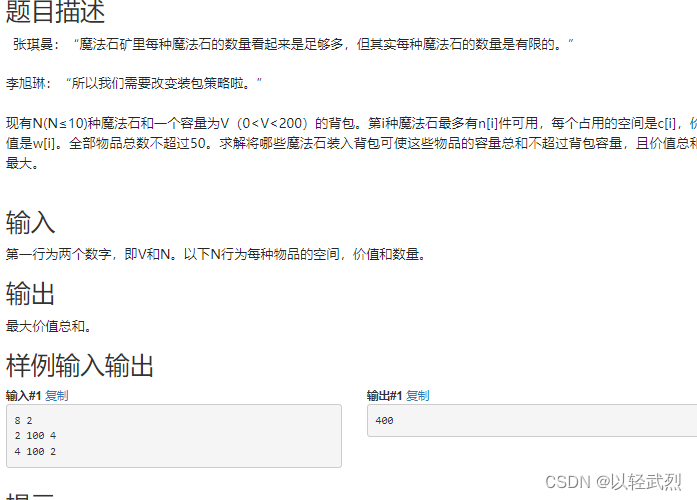
3155 多重背包

方法一
转化为普通的01背包
思路：把每种有n个的物品看成是n件一个物品，转化为01背包

#include<bits/stdc++.h>
using namespace std;
int f[5005],n,m,w[2005],v[2005],cnt,V,W,s;
int main()    {
    cin>>m>>n;
    for (int i=1;i<=n;++i)    {
        cin>>V>>W>>s;
        for (int j=1;j<=s;++j)    {
            cnt++;
            v[cnt]=V;
            w[cnt]=W;
        }
    }
    for (int i=1;i<=cnt;++i)    {
        for (int j=m;j>=v[i];--j)    {
            f[j]=max(f[j-v[i]]+w[i],f[j]);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

方法二
利用二进制的优化，转化为01背包
把有n件的物品拆分成1件，2件，4件，8件……2的k次方件，n-2的k次方件。事实证明，这样既可以获得全部的拆分方案，又同时不会超过n件，这对于上一种方法是很大的改进。

#include<bits/stdc++.h>
using namespace std;
int f[5005],n,m,w[2005],v[2005],cnt,V,W,s;
int main()    {
    cin>>m>>n;
    for (int i=1;i<=n;++i)    {
        cin>>V>>W>>s; 
        int j=1;
        while (j<=s)    {
            s-=j;
            cnt++;
            v[cnt]=V*j; 
            w[cnt]=W*j; 
            j<<=1;
        }
        if (!s)    continue;//排除掉取0件
        cnt++;
        v[cnt]=V*s; 
        w[cnt]=W*s;
    }
    for (int i=1;i<=cnt;++i)    {
        for (int j=m;j>=v[i];--j)    {
            f[j]=max(f[j-v[i]]+w[i],f[j]);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

方法三
单调队列
如果只考虑NOIP范围内的话，方法二已经很优了。但是用单调队列来解决多重背包问题，可以效率更高。这里就不给大家展示代码了，大家可以自行摸索。