运筹说 第96期 | 非线性规划基本概念

一、前言

1 发展历程

非线性规划是具有非线性约束条件或目标函数的数学规划，是运筹学的重要分支，是20世纪50年代才开始形成的一门新兴科学。

2 非线性规划与线性规划的区别

1. 目标约束不同：线性规划的目标函数和约束条件都是其自变量的线性函数（一次式）；非线性规划的目标函数和约束条件都是其自变量的非线性函数（含有非线性成分）。
2. 最优解范围不同：如果最优解存在，线性规划只能存在可行域的边界上找到；非线性规划的最优解可能存在于可行域的任意一点。

3 经典方法

1. 一维最优化方法：黄金分割法，切线法，插值法
2. 无约束最优化方法：梯度法，牛顿法，共轭梯度法，拟牛顿法
3. 约束最优化方法：制约函数法，可行方向法

二、基本概念

1 非线性规划的数学模型

一般形式

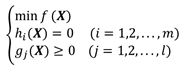
无等式形式

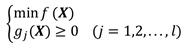
若存在等式，可用

代替

可行域形式

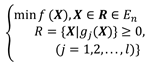
2 二维问题的图解

当只有两个自变量时，求解非线性规划也可像对线性规划那样求助于图解法。对于下述非线性规划问题，第一个约束为图中抛物线左边的部分，第二个约束为直线上侧部分，然后考虑到自变量的非负约束，得到模型的可行域。因此目标函数最终可转化为求解可行域内点到(2,1)的最短距离。

3 局部极小与全局极小

设𝑓(𝑿)为定义在𝑛维欧氏空间En的某一区域𝑅上的𝑛元实函数。

（1）局部极小

对于X*∈R，如果存在某个ε>0，使所有与X*的距离小于ε的X∈R，都有f(X)≥fX*，则称X*为fX

在R上的局部极小点，fX*为局部极小值。

若对于所有X≠X*且与X*的距离小于ε的X∈R，都有fX>fX*，则称X*为fX在R上的严格局部极小点，fX*为严格局部极小值。

（2）全局极小

如果存在X*∈R，对所有X∈R都有fX≥fX*，则称X*为fX在R上的全局最小点，fX*为全局最小值。

若对于所有X∈R且X≠X*，都有fX>fX*，则称X*为fX在R上的严格全局最小点，fX*为严格全局最小值。

4 多元函数极值点存在的条件

（1）必要条件

定理1：设R是n维欧氏空间En上的某一开集，f(X)在R上有连续一阶偏导数，且在点X*∈R

取得局部极值，则必有

或写成

此处

为函数f(X)在点X*处的梯度。

（2）二次型

二次型是X=x1,x2,…,xnT的二次齐次函数

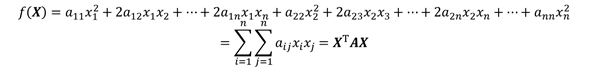
其中，aij= aji，A为n×n对称矩阵。若A所有元素都是实数，则称为实二次型。

二次型的类型主要包括：正定、负定、不定、半正定、半负定。其中，实二次型XTAX正定的充要条件为A左上角各阶主子式都大于零，半正定各阶主子式大于等于零；实二次型XTAX负定的充要条件为A左上角各阶主子式负正相间，半负定各阶主子式“≤≥”相间。

（3）多元函数的泰勒公式

在X(0)处的泰勒展开式：

其中，

若以X=X0+P代入，则展开式变为：

其中，

也可写成含高阶无穷小形式：

其中，当X→X0时，ο(X-X(0)2)为X-X(0)2的高阶无穷小。

（4）充分条件

定理2：设R是n维欧式空间En上的某一开集，fX在R上有连续二阶偏导数，若?fX*=0，且?2fX*正定，则X*∈R为fX的严格局部极小点。此处，称纳布拉fX*的矩阵式为黑塞矩阵。

5 凸函数和凹函数

（1）定义

设fX为定义在n维欧氏空间En中某个凸集Rc上的函数，若对任何实数α0<α<1以及Rc中的任意两点X1和X(2)，恒有

则称f(X)为定义在Rc上的凸函数。

若对任何实数α0<α<1以及Rc中的任意两点X1和X(2)，恒有

则称f(X)为定义在Rc上的严格凸函数。

若两式中的不等号反向，即可得到凹函数和严格凹函数的定义。显然，若函数f(X)=-g(X)是凸函数(严格凸函数)，则g(X)一定是凹函数(严格凹函数)。

【几何意义】

函数图形上的任意两点的连线都在这个图形的上方，就是向下凸的。凹函数则是向下凹的。

（2）性质

1. 性质1：设f(X)为定义在凸集Rc上的凸函数，则对任意实数β≥0,函数βf(X)也是定义在Rc上的凸函数。
2. 性质2：设f1(X)和f2(X)为定义在凸集Rc上的两个凸函数，则这两个凸函数的和fX=f1X+f2(X)仍为定义在Rc上的凸函数。

由以上两个性质可以推得：有限个凸函数的非负线性组合

仍为凸函数。

1. 性质3：设f(X)为定义在凸集Rc上的凸函数，则对每一实数β，集合(称为水平集)

是凸集。

（3）凸函数的判定

【一阶条件】

设R为En上的开凸集，f(X在Rc上可微，则f(X)为Rc上的凸函数的充要条件是：对任意不同两点X(1)∈Rc和X(2)∈Rc，恒有

若上式为严格不等式，它就是严格凸函数的充要条件。如将上式中的不等号反向，就可得到凹函数(严格不等号时为严格凹函数)的充要条件。

【二阶条件】

设Rc为En上的开凸集，f(X)在Rc上二阶可微，则f(X)为Rc上的凸函数(凹函数)的充要条件是：对所有X∈R?，其黑塞矩阵半正定(半负定)。

若f(X)的黑塞矩阵对所有X∈R，都是正定(负定)的，则f(X)是Rc上的严格凸函数(严格凹函数)。

（4）凸函数的极值

现设fX是定义在凸集Rc上的可微凸函数，如果存在点X*∈Rc，都有

则X*就是fX在Rc上的最小点（全局最小点）。

6 凸规划

对于非线性规划式

若其中的f(X)为凸函数，giX(j=1,2,?l)全为凹函数，则此非线性规划为凸规划，即

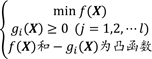
凸规划具有以下性质：

1. 可行解集为凸集。
2. 最优解集为凸集(假定最优解存在)。
3. 任何局部最优解也是其全局最优解。
4. 若目标函数为严格凸函数，且最优解存在，则其最优解必唯一。

7 下降迭代算法

（1）基本思想

按照一定的规则（算法）逐步迭代寻找更优点，得到一个解点的序列X(k)，若该点列有一极限点X*，即

则称该点列收敛于X*。

对于极小化问题而言，我们要求解的序列X(k)，其对应的目标函数值fX(k)应是逐步减小的，即要求

具有这种性质的算法称为下降迭代算法

（2）一般迭代格式

1. 选取某一初始点X(0)，令k:=0。
2. 确定搜索方向。当已得出某一迭代点X(k)，且X(k)不是极小点。这时，就从X(k)出发确定一搜索方向P(k),要求沿着这个方向可以找到能使目标函数值下降的点。
3. 确定步长。沿P(k)方向前进一个步长，得到新点X(k+1)。即在由X(k)出发的射线X=X(k)+λPk(λ≥0)上，通过确定步长（因子）λ=λk得下一个迭代点X(k+1)=X(k)+λkPk,使得fX(k+1)=fX(k)+λkPk<fX(k)
4. 检验新得到的点是否为要求的极小点或近似极小点。如满足要求，迭代终止。否则令k:=k+1，返回第2步继续迭代。

（3）步长选定

在极小化问题中，步长的选定由使目标函数值沿搜索方向下降最多为依据的，即沿射线X(k)+λP(k)求f(x)的极小，即选取λk使

称此过程为一维搜索/线搜索，由此确定的步长为最佳步长。

定理3：设目标函数𝑓(𝑋)具有连续一阶偏导数，X(k+1)按下述规则产生：

则有

即搜索方向上所得最优点处的梯度和该搜索方向正交。这可以用来判断是否达到终止迭代的要求。

（4）常用的终止迭代准则

根据相继两次迭代结果的绝对误差：

根据相继两次迭代结果的相对误差：

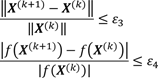
根据函数梯度的模足够小：

其中，上述三式要求分母不等于和不接近于零，各式中的ε1、ε2、ε3、ε4和ε5为足够小的正数。