数据结构：栈和队列

王有志，一个分享硬核Java技术的互金摸鱼侠
加入Java人的提桶跑路群：共同富裕的Java人

今天我们来学习线性表中最后两种数据结构：栈和队列。它们是两种比较特殊的线性表，相较于数组和链表而言，可以认为它们是“高级”的线性表。

栈和队列的特点

前几天和媳妇聊到大学校门口的美食广场，每到夜晚便人声鼎沸，撸肉串的，喝扎啤的……
Hold on！Hold on！(最近沉迷《中国说唱巅峰对决》hhh)。
羊肉串和扎啤不就是栈和队列吗？你品，你细品。
串肉串的时候，从签子的尖头（栈顶）开始串（入栈），最先串进去的被压倒签子的底部（栈底），而撸串（出栈）也是从尖头开始，最后串进去的却最先被吃掉（后进先出，LIFO，last in first out）。
灌扎啤的时候，从灌口（队尾）灌进去（入队）的扎啤停留在罐底（队首），当你从罐底的水龙头打开的时候，最先流出来（出队）的停留在罐底的那部分（先进先出，FIFO，first in first out）。
我们再来画张图，来看看栈和队列到底“长什么样”。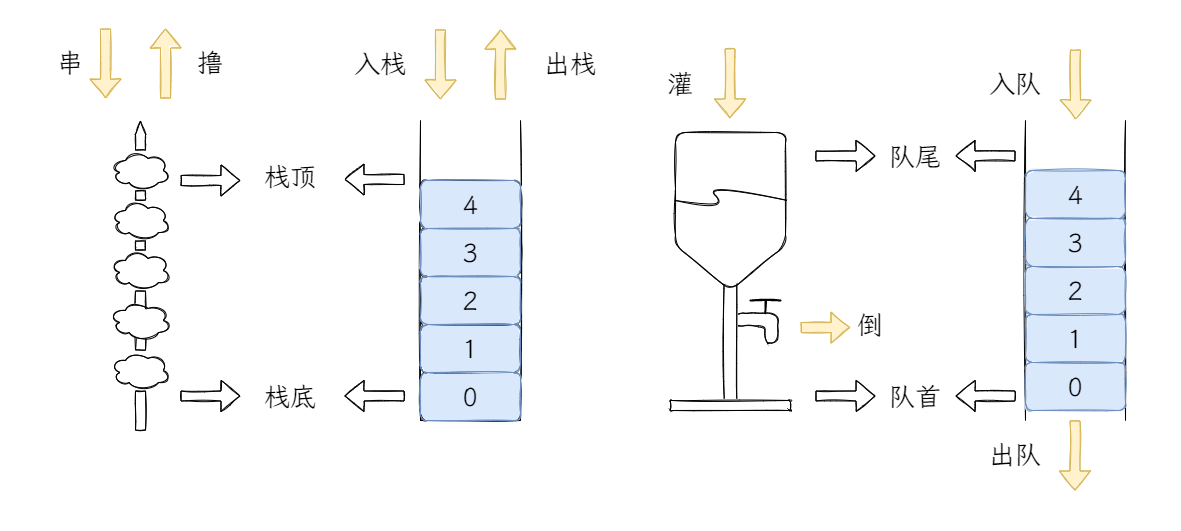

看起来栈和队队列就是很普通的线性表啊，没什么特别的。
实际上就是这样的，如果限定数组或链表只能在尾部插入和尾部删除，那就是栈。如果只能在头部删除尾部插入，那就是队列。
也正是如此，我们常常称栈和队列为受限线性表，数组和链表为非受限线性表。而栈和队列所允许的操作也是数组和链表所允许操作的子集。

栈和队列的ADT

了解了栈和队列后，我们来看看它们都允许哪些操作，这里我们“抄袭”Java中方法的命名习惯给出对应数据结构的ADT，首先是栈：

public interface Stack<E> {

	/**
   * 大小
   */
	int size();

	/**
   * 是否为空
   */
	boolean isEmpty();

	/**
   * 入栈
   */
	void push(E e);

	/**
   * 出栈
   */
	E pop();

	/**
   * 查看栈顶数据
   * 与{@link Stack#pop()}的区别是：
   * pop会移除栈顶数据
   * peek不会移除栈顶数据
   */
	E peek();
}

接着是队列：

public interface Queue<E> {

	/**
   * 大小
   */
	int size();

	/**
   * 是否为空
   */
	boolean isEmpty();

	/**
   * 入队
   */
	void add(E element);

	/**
   * 出队
   */
	E poll();

	/**
   * 查看队首数据
   * 与{@link Queue#poll()}的区别是：
   * poll会移除队首数据
   * peek不会移除队首数据
   */
	E peek();
}

相较于动态数组和链表，栈和队列的操作就简单很多了，实现起来也非常容易，在这里就不水字数了。你可以基于已经实现过的动态数组和链表去实现，也可以自行实现顺序结构或者链式结构。
附上我实现的栈和队列，欢迎大家一起讨论。

栈的应用

栈这种结构虽然简单，但是在计算机世界中却有着极其重要的作用，其中最耳熟能详的就是调用栈了。
如果对调用栈不熟悉的小伙伴，推荐阅读汤洋老师的文章《Call Stack（调用栈）是什么？》。

调用栈

如果你是Java程序员，相信在面试中你一定被问到过虚拟机栈。没错，Java中的虚拟机栈就是最典型的调用栈之一。
还记得我们在编程技巧：从斐波那契数列到递归中说到尾递归消除时的那张图吗？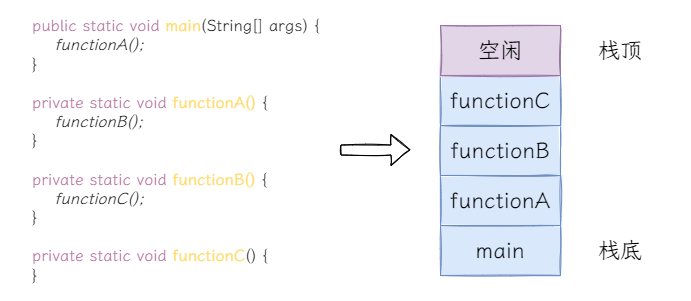

main中调用functionA，functionA调用functionB，functionB调用functionC，每次调用后都压入到栈中，按照代码的执行逻辑，functionC最先执行完毕，可以从栈中取出，然后functionB，functionA和main。
现在来看，栈的特性是不是完美契合计算机中的调用顺序？

撤销栈

作为一名资深的“CV工程师”，除了Ctrl+C和Ctrl+V外，我还会经常使用Ctrl+Z，毕竟谁也不能保证绝对不出错嘛。
不过，你有没有思考过计算机是怎么知道撤销哪一步操作呢？
其实很简单，计算机使用栈这种结构记录每一步操作，假如我们分别输入“曾经”，“沧海”，“难为水”，当我们输入完成后，发现“难为水”写成了“难为谁”（可能是输入法不够智能）。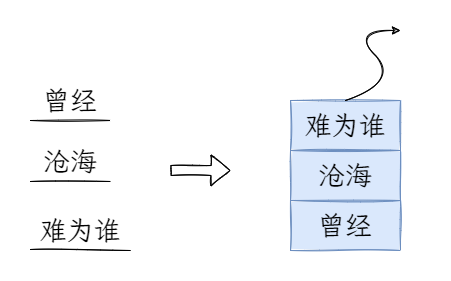

当我们按下Ctrl+Z时，计算机只需要将撤销栈中栈顶数据对应的输入删除就可以实现撤销最近一次操作了。

逆波兰式

逆波兰式又称为后缀表达式，当然有后缀表达式就有前缀表达式（也称为波兰式），既然前后都有了，那也有中缀表达式。
假如我们有一道算术题：$(1+3)\times (4?2)$。
相信你可以很轻松的告诉我答案，但对于计算机来说，这太复杂了，既有括号，又有乘法，加法，优先级都搞不明白，还要怎么计算？不过也不是没有办法。

逆波兰表示法（Reverse Polish notation，RPN，或逆波兰记法），是一种是由波兰数学家扬·武卡谢维奇1920年引入的数学表达式形式，在逆波兰记法中，所有操作符置于操作数的后面，因此也被称为后缀表示法、后序表示法。逆波兰记法不需要括号来标识操作符的优先级。

逆波兰结构由弗里德里希·鲍尔（Friedrich L. Bauer）和艾兹格·迪科斯彻在1960年代早期提议用于表达式求值，以利用堆栈结构减少计算机内存访问。逆波兰记法和相应的算法由澳大利亚哲学家、计算机学家查尔斯·汉布尔（Charles Hamblin）在1960年代中期扩充。
在1960和1970年代，逆波兰记法广泛地被用于台式计算器，因此也在普通公众（如工程、商业和金融等领域）中使用。
以上来自维基百科逆波兰表示法词条，能够科学上网的小伙伴可以自行阅读。
所以上面的题目在逆波兰表达式中为：$13+42?\times$。
你发现没有，在逆波兰式和栈结合后，计算机不需要在考虑括号对运算优先级的提升了，这样计算机就可以快速计算了。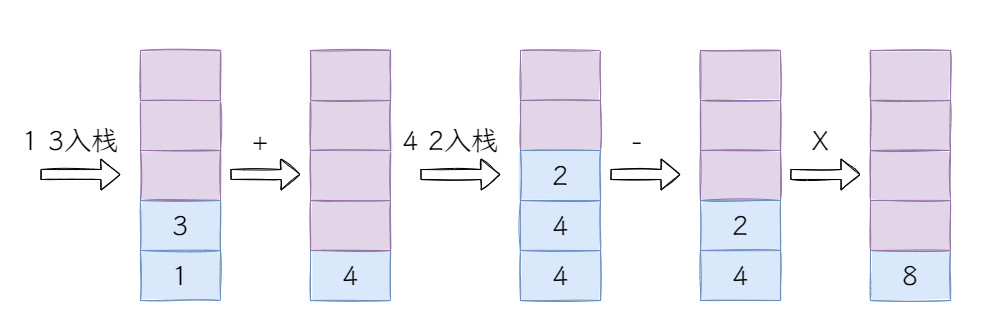

简单描述逆波兰式的算法过程为，数字按顺序压入栈，遇到符号时弹出栈顶的两个数字进行计算。
大概原理是这么简单，不过实际处理起来还是比较复杂的，这里附上我实现的简易版逆波兰式算法(没有中缀表达式的转换过程，没有处理任何边界情况)。

循环队列

使用数组实现队列时，出队不得不移动数据以保证下次依旧可以通过下标0取得数据，因此，出队操作的时间复杂度是O(n)，显然是有点慢了。
如果我们换一个角度思考，为了保证下标0可持续使用，而移动数据代价是不是太大了？可不可以改变下标，而不移动数据呢？
答案是肯定的，我们可以不断改变队首的位置，而非移动数据来保证队首始终在下标为0的位置。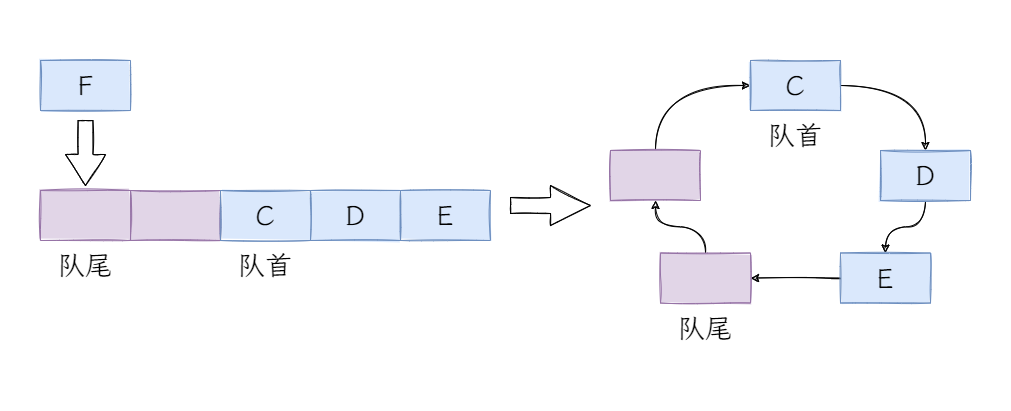

每次出队后指向队首的指针向后移动一位，入队后指向队尾的指针同样向后移动一位。这样，在不考虑超出数组容量的前提下，可以循环往复的使用数组中的内存，当然超过了就需要考虑扩容和重排队列数据了。
既然知道了基本原理，相信你可以很轻松的实现循环队列，提供我实现的循环队列作为参考，欢迎大家一起讨论。

结语

今天我们一起学习了栈和队列，它们是线性表中比较特殊的存在，如果要给线性表划分层级的话，基础的是数组和链表，在此之上我们可以构建出“更高级”的栈和队列。
在通过生活中的例子解释了栈和队列后我们学习了栈在计算机世界中丰富的应用，以及一种的队列–循环队列。
到今天为止线性表中比较基础的内容已经结束了，如果想要彻底的掌握它们还需要勤加练习。接下来，我们就要开始树的学习了，各位小伙伴们加油。

练习

• 实现栈和队列
• 实现循环队列
• 剑指 Offer 06.从尾到头打印链表
• 剑指 Offer 09.用两个栈实现队列
• 剑指 Offer 50.第一个只出现一次的字符
• 20.有效的括号
• 933.最近的请求次数

---

如果本文对你有帮助的话，还请多多点赞支持。如果文章中出现任何错误，还请批评指正。最后欢迎大家关注分享硬核Java技术的金融摸鱼侠王有志，我们下次再见！