【Py/Java/C++三种语言详解】LeetCode每日一题240122【贪心】LeetCode670、最大交换

题目链接

LeetCode670、最大交换

题目描述

给定一个非负整数数组 nums 和一个整数 k ，你需要将这个数组分成 k 个非空的连续子数组。

设计一个算法使得这 k 个子数组各自和的最大值最小。

示例 1：

输入：nums = [7,2,5,10,8], k = 2
输出：18
解释： 一共有四种方法将 nums 分割为 2 个子数组。 其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。 因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

示例 2：

输入：nums = [1,2,3,4,5], k = 2
输出：9

示例 3：

输入：nums = [1,4,4], k = 3
输出：4

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 10(6)
• 1 <= k <= min(50, nums.length)

解题思路

数据范围（数字的长度）最大为8，时间复杂度为O(N^3)的暴力法可以通过。

所谓暴力法，就是枚举出所有不同的下标对(i, j)，交换s[i]和s[j]，找到交换完之后最大的那一组。

思路较为简单，故在此略去不表。一下讨论贪心的做法。

为什么是贪心

由于最多只能交换一次，贪心地思考一下这个问题：我们什么希望进行一个怎么样的交换？

换言之，怎么交换才能使得数字尽可能地大？

考虑例子

9091987

原字符串中的第三个"9"是最大且位置尽可能靠后的数字，这个字符应该优先地被交换到尽可能前的位置。由于索引0的数字是"9"，所以考虑索引1的字符"0"和第三个"9"交换。得到答案

9991087

从这个例子可以看出贪心的策略是：

1. 首选一个尽可能大的数字（比如示例中选择字符"9"）
2. 如果有多个最大的数字，则优先选择位置尽可能靠后的那个（比如示例中选择第三个"9"）
3. 将该数字交换到尽可能靠前的位置，即交换到第一个小于该数字的位置（比如示例中索引1的位置）。

所以考虑逆序遍历原数字字符串（为了方便交换操作，改成数组来操作），并且使用一个栈（类似一个单调栈），储存原数字从右往左看遇到的更大的数字的下标

stack = list()
for i in range(n-1, -1, -1):
    if not stack or lst[i] > lst[stack[-1]]:
        stack.append(i)

最终这个栈一定会满足以下条件：

• 栈中储存的是原数字字符串的数字的下标i
• i的取值自栈底向栈顶递减，即栈顶元素stack[-1]是在数字lst中位置最靠前的下标（满足了上述贪心策略2）
• lst[i]的取值自栈底向栈顶递增，即栈顶元素对应的下标在数字数组中的取值lst[i]是最大的数字（满足了上述贪心策略1）

以例子num = 9091987为例，栈中的结果是储存了最后三个数字"987"的下标，即stack = [6, 5, 4]

接下来要考虑如何实现上述贪心策略的第三点。

我们可以从头到尾遍历原数字数组lst，将下标i和栈顶元素stack[-1]、以及下标i对应的数字lst[i]和栈顶元素对应的数字lst[stack[-1]]进行比较。若

• i < stack[-1]，说明此时下标i的位置位于stack[-1]的左边，可以继续进行后续判断。若
  • lst[i] < lst[stack[-1]]，说明此时可以交换位置i和stack[-1]的两个数字，交换之且退出循环
  • lst[i] >= lst[stack[-1]]，说明此时不能进行交换，i需要继续增大
• i >= stack[-1]，说明此时下标i的位置已经不再位于stack[-1]的左边，此时不能再考虑栈顶元素，应该将其弹出

另外，由于涉及弹出操作，如果出现空栈情况，但尚未进行交换，则说明原数字数字本身就是一个非递增序列，需要退出循环。综上，上述贪心操作的代码为

for i in range(n):
    if not stack:
        break
    if i > stack[-1]:
        if lst[i] < lst[stack[-1]]:
            lst[i], lst[stack[-1]] = lst[stack[-1]], lst[i]
            ans = "".join(lst)
            break
        else:
            continue
    else:
        stack.pop()

一个带图的例子

再举一个例子，num = "9987687676"，答案应该为ans = "9988677676"，可以做出如下图

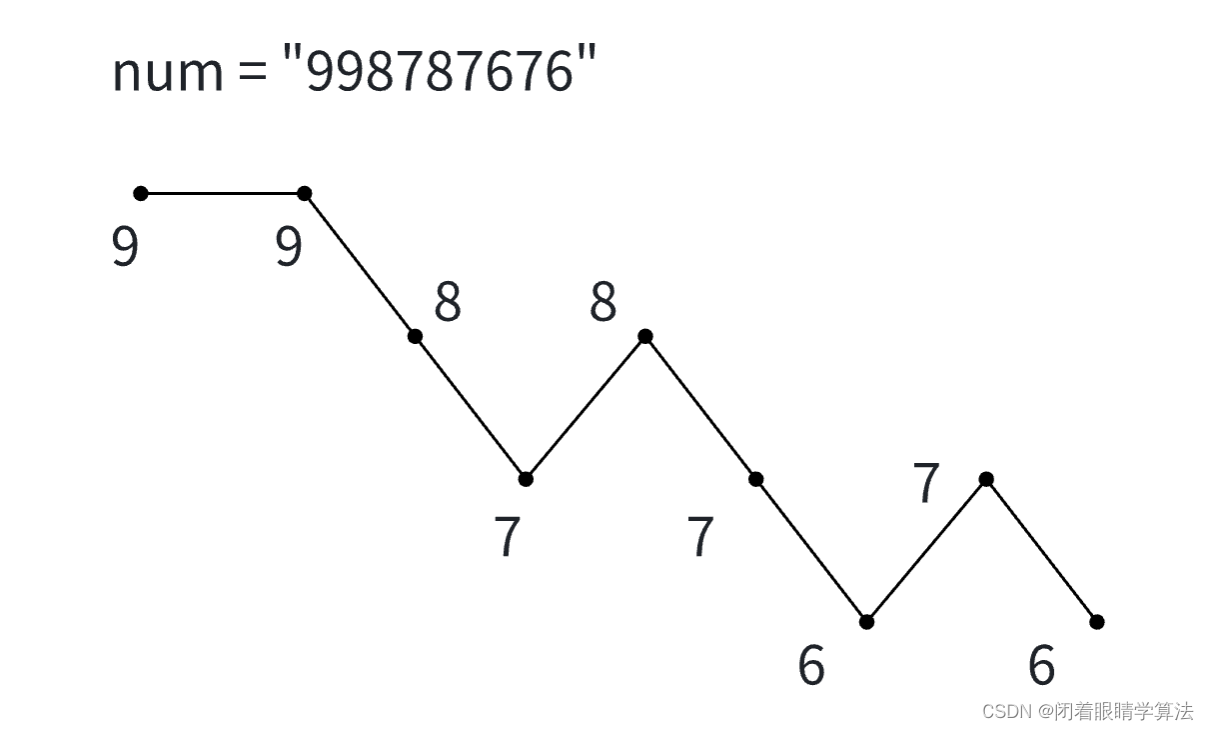
逆序遍历数组lst，构建栈stack = [8, 7, 4, 1]，为可能进行交换的那些对应较大数字且靠后的位置。

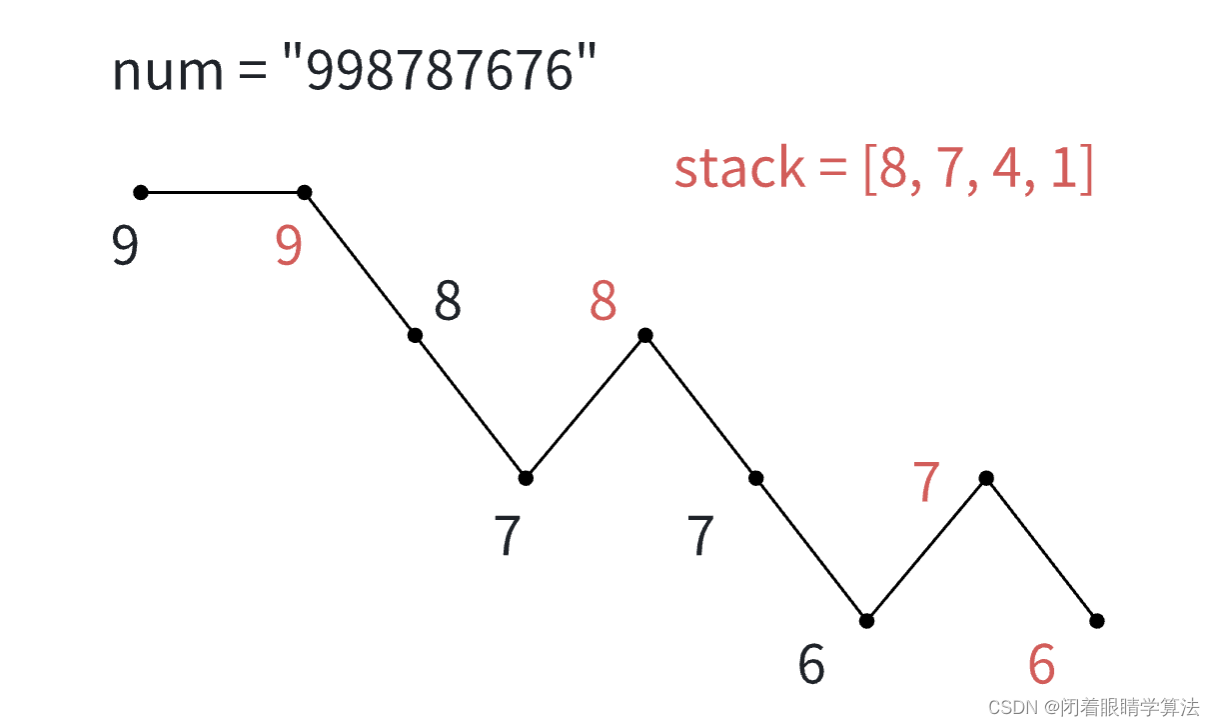
正序遍历i，反复拿出栈顶索引对应的元素lst[stack[-1]]对应的数字和i对应的元素lst[i]进行比较。会经历如下过程。

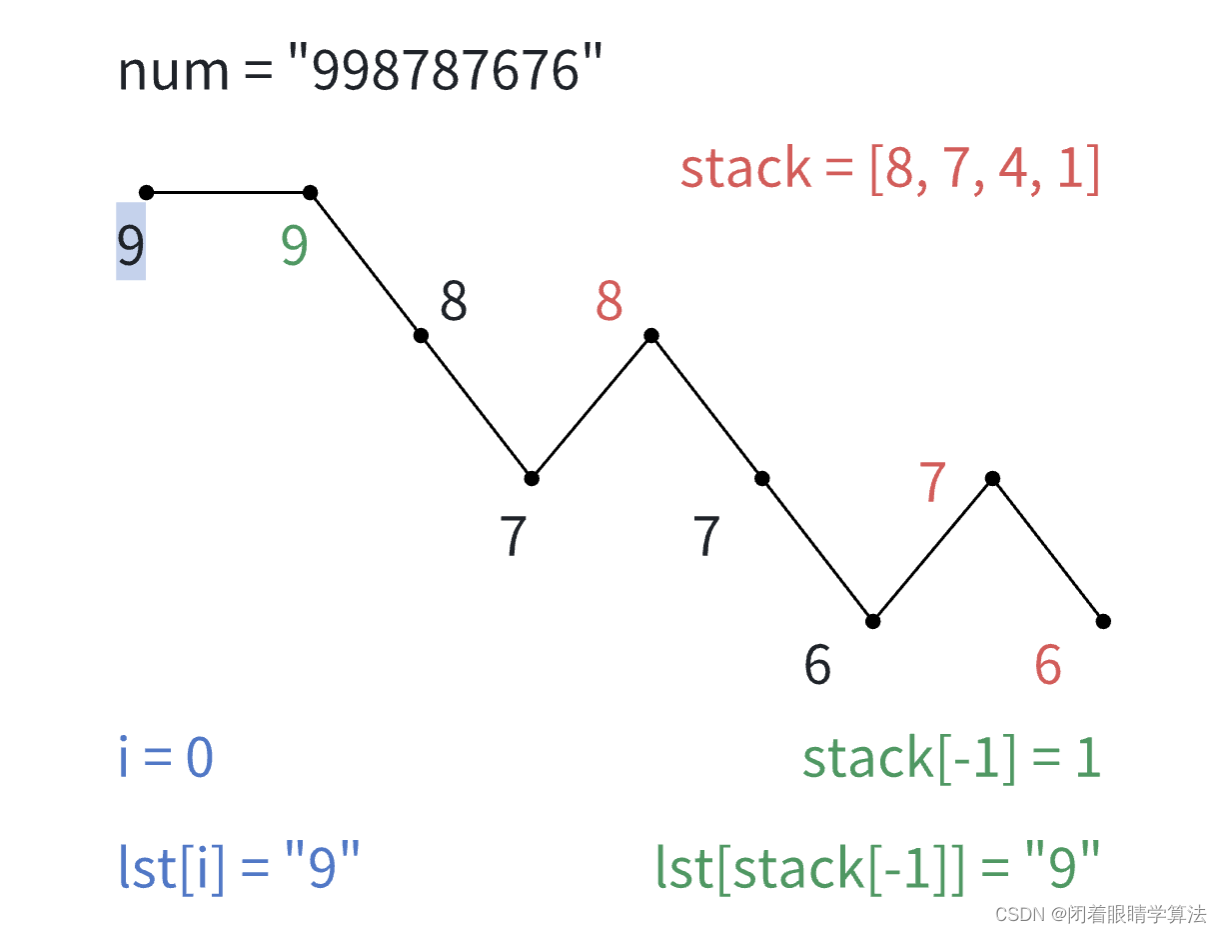
i < stack[-1]，但lst[i] >= lst[stack[-1]]。不能做交换，i增加。

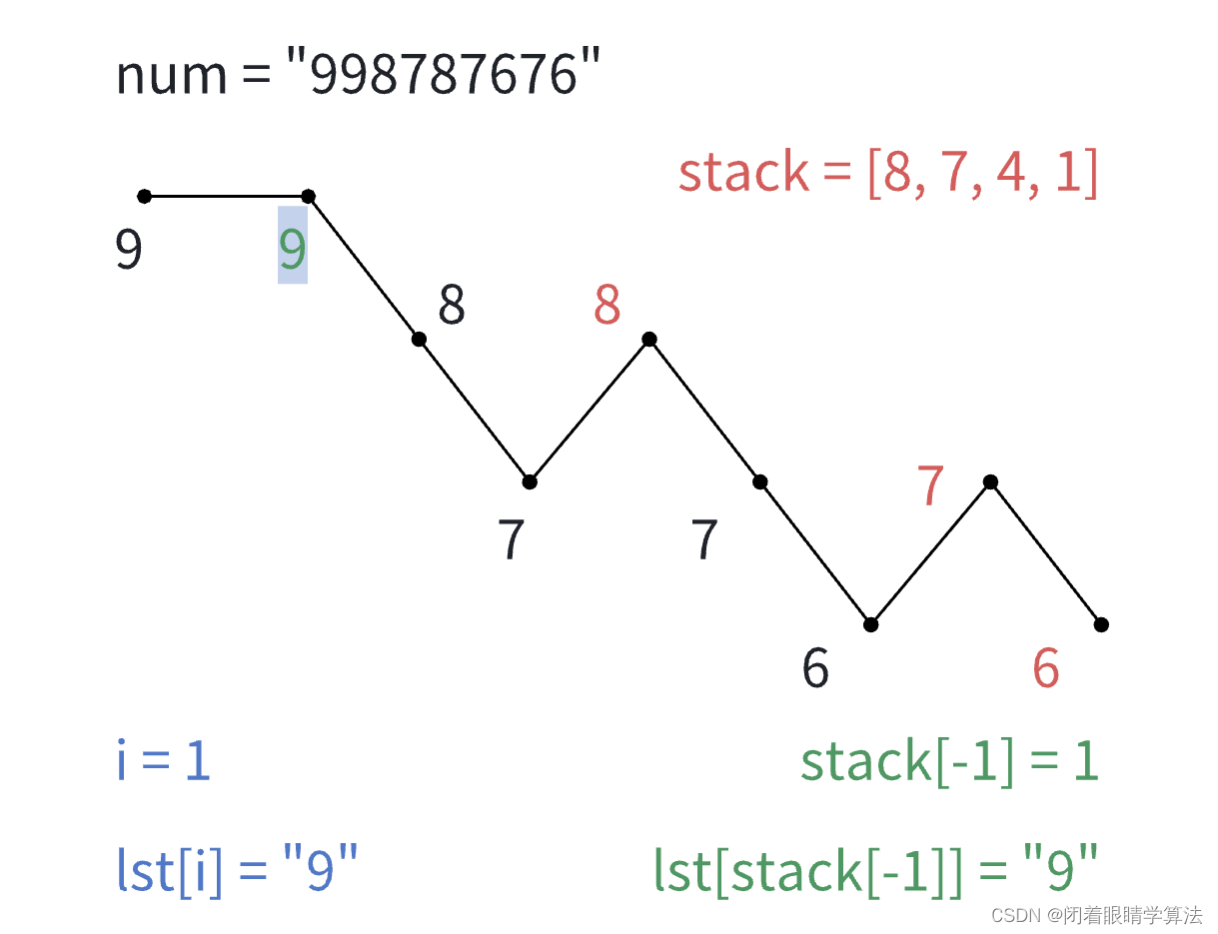
i >= stack[-1]，即i的位置不位于stack[-1]的左边，stack[-1]出栈，i增加。

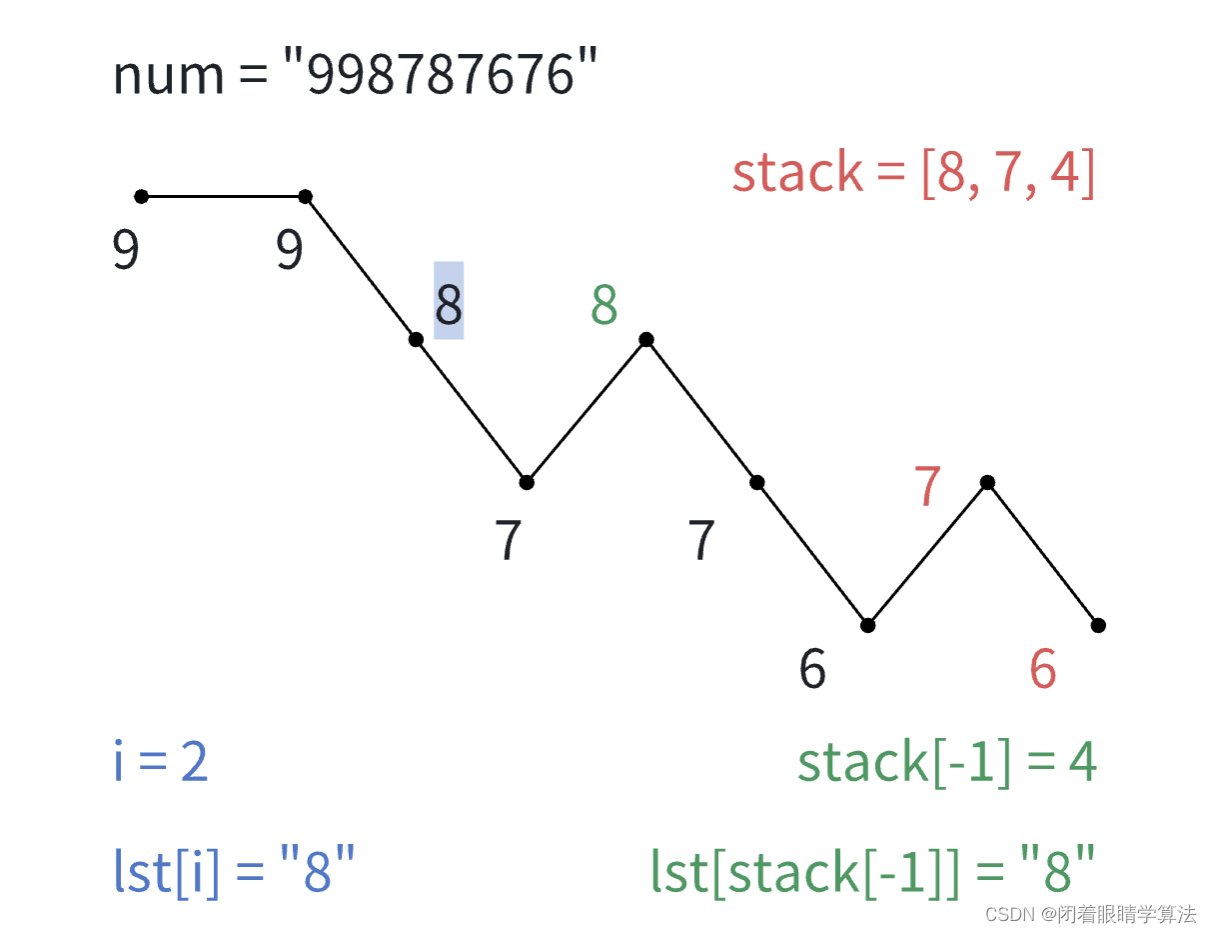
i < stack[-1]，但lst[i] >= lst[stack[-1]]。不能做交换，i增加。

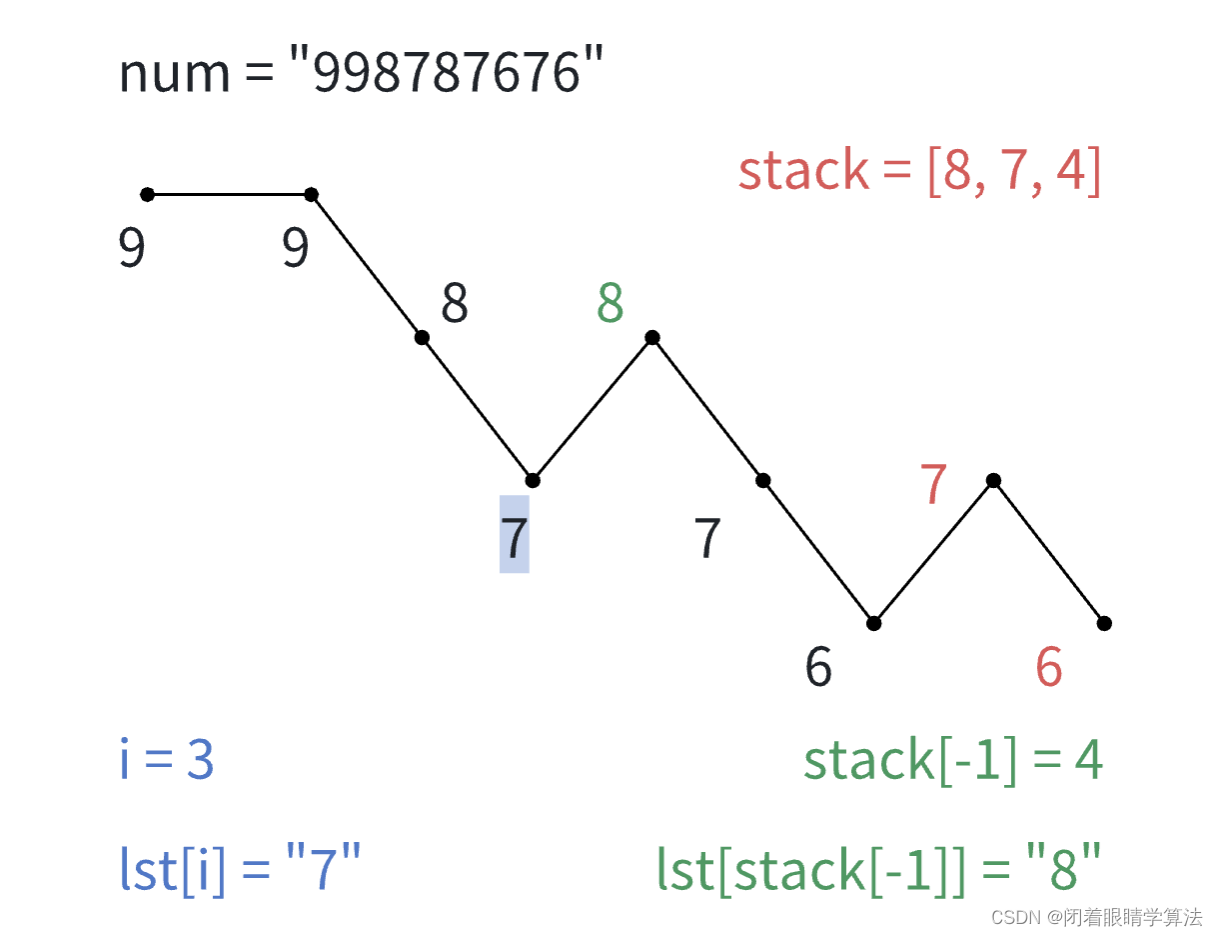
i < stack[-1]，且lst[i] < lst[stack[-1]]。进行交换，得到ans = "9988677676"，是可以得到的数字最大的结果。

代码

python

# 贪心+栈：O(N)
class Solution:
    def maximumSwap(self, num: int) -> int:
        # 用列表的形式储存数字num
        lst = list(str(num))
        # 获得数字num的位数（即lst的长度）
        n = len(lst)

        # 构建一个栈，储存原字符串从右往左看遇到的更大数字的下标
        stack = list()

        # 逆序遍历字符串s
        for i in range(n-1, -1, -1):
            # 如果栈是空栈，或者当前下标i对应的数字lst[i]大于栈顶下标对应的数字lst[stack[-1]]
            # 则将索引i加入stack
            if not stack or lst[i] > lst[stack[-1]]:
                stack.append(i)
        
        # 正序遍历列表lst
        for i in range(n):
            # 若出现空栈情况，则退出循环
            if not stack:
                break
            # 如果当前下标i位于栈顶元素stack[-1]的左边
            # 则可以进行后续判断
            if i < stack[-1]:
                # 若当前数字小于栈顶元素对应的数字，则可以进行交换
                if lst[i] < lst[stack[-1]]:
                    lst[i], lst[stack[-1]] = lst[stack[-1]], lst[i]
                    return int("".join(lst))
                # 否则，考虑下一个i，这里的else也可以不写
                else:
                    continue
            # 如果当前下标i不位于栈顶元素stack[-1]的左边
            # 则弹出栈顶元素，考虑下一个较小但是位于较右位置的数字
            else:
                stack.pop()

        return num
                

java

public class Solution {
    public int maximumSwap(int num) {
        char[] chars = Integer.toString(num).toCharArray();
        int n = chars.length;
        int[] stack = new int[n];

        int top = -1;
        for (int i = n - 1; i >= 0; i--) {
            if (top == -1 || chars[i] > chars[stack[top]]) {
                stack[++top] = i;
            }
        }

        for (int i = 0; i < n; i++) {
            if (top == -1) {
                break;
            }

            if (i < stack[top]) {
                if (chars[i] < chars[stack[top]]) {
                    char temp = chars[i];
                    chars[i] = chars[stack[top]];
                    chars[stack[top]] = temp;
                    return Integer.parseInt(new String(chars));
                }
            } else {
                top--;
            }
        }

        return num;
    }
}

cpp

class Solution {
public:
    int maximumSwap(int num) {
        std::string numStr = std::to_string(num);
        int n = numStr.length();
        std::vector<int> stack;

        for (int i = n - 1; i >= 0; i--) {
            if (stack.empty() || numStr[i] > numStr[stack.back()]) {
                stack.push_back(i);
            }
        }

        for (int i = 0; i < n; i++) {
            if (stack.empty()) {
                break;
            }

            if (i < stack.back()) {
                if (numStr[i] < numStr[stack.back()]) {
                    std::swap(numStr[i], numStr[stack.back()]);
                    return std::stoi(numStr);
                }
            } else {
                stack.pop_back();
            }
        }

        return num;
    }
};

时空复杂度

时间复杂度：O(N)。仅需一次遍历所有数字。

空间复杂度：O(1)。栈所占空间，最大为9，可视为常数级别空间。

---

华为OD算法/大厂面试高频题算法练习冲刺训练

• 华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务100+同学成功上岸！

• 课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

• 每期人数维持在20人内，保证能够最大限度地满足到每一个同学的需求，达到和1v1同样的学习效果！

• 60+天陪伴式学习，40+直播课时，300+动画图解视频，300+LeetCode经典题，200+华为OD真题/大厂真题，还有简历修改、模拟面试、专属HR对接将为你解锁

• 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

• 可查看链接 大厂真题汇总 & OD真题汇总(持续更新)

• 绿色聊天软件戳 od1336了解更多