2023年泰迪杯数据分析赛a题解析（二）

任务 2 数据分析与可视化

任务 2.1 计算并绘制每天不同工序完成案卷数量的簇状柱形图：x 轴表示时间，y 轴 表示完成案卷的数量，用不同颜色标记不同工序。

计算并绘制每天不同工序完成案卷数量的簇状柱形图：x 轴表示时间，y 轴 表示完成案卷的数量，用不同颜色标记不同工序。

提取所需要的数据并提取出每个工序的日期，就保留日期即可；然后统计每个工序的值计数，作为一个Series放回，将日期进行升序排序并转为数据框，最后是合并数据框进行重命名。画图部分对x轴为时间序列，设置宽度和画布，y轴为各个序列的值，最后设置标题和标签即可。

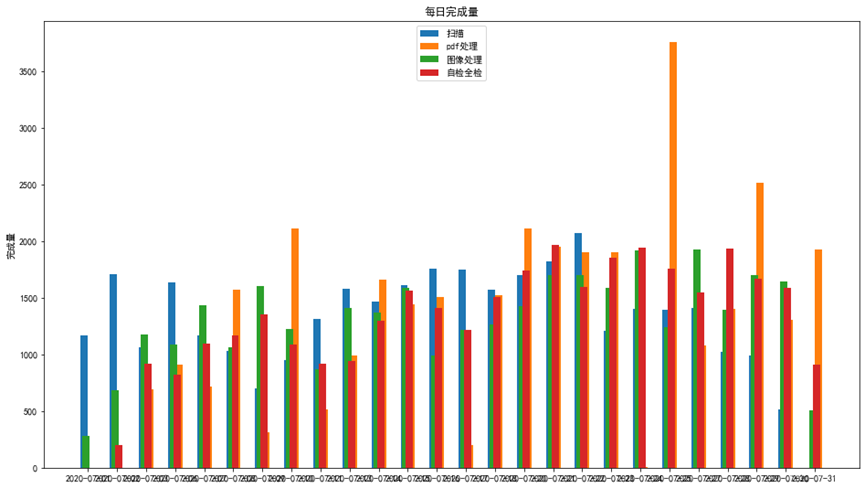
本图统计了每天不同工序完成案卷数量的簇状图，从中可以看出扫描每天的完成量基本上都算比较高的，每天的量也挺大，pdf处理是每周呈现递增趋势，周五，周六的值最高，图像处理也是每周呈现递增趋势，值到后面越来越高，自检全检保存在一个比较平均的值除了7月1号和2号两天不同。

重要代码展示：

# 设置matplotlib支持中文显示
plt.rcParams['font.sans-serif']=['SimHei']

# 定义x轴日期标签  


labels=['2020-07-01', '2020-07-02', '2020-07-03', '2020-07-06', '2020-07-07', '2020-07-08',
       '2020-07-09', '2020-07-10', '2020-07-11', '2020-07-13', '2020-07-14', '2020-07-15',
       '2020-07-16', '2020-07-17', '2020-07-18', '2020-07-20', '2020-07-21', '2020-07-22',
       '2020-07-23', '2020-07-24', '2020-07-25', '2020-07-27', '2020-07-28', '2020-07-29',
       '2020-07-30', '2020-07-31']
# 生成x轴位置数组
x = np.arange(len(labels))  

# 设置bar图宽度
width = 0.25

# 绘制图形  
fig, ax = plt.subplots(figsize=(16,9))

# 绘制扫描部分条形图
rects1 = ax.bar(x - width/2, data1['saodata'], width, label='扫描')

# 绘制PDF处理部分条形图  
rects2 = ax.bar(x + width/2, data1['pdfdata'], width, label='pdf处理') 

# 绘制图像处理部分条形图
rects3 = ax.bar(x - width/4, data1['pictdata'], width, label='图像处理')

# 绘制自检全检部分条形图
rects4 = ax.bar(x + width/4, data1['jiandata'], width, label='自检全检')

# 添加标签、标题等
ax.set_ylabel('完成量')
ax.set_title('每日完成量')

# 设置x坐标刻度点与标签
ax.set_xticks(x)
ax.set_xticklabels(labels)

# 添加图例
ax.legend()

任务 2.2 计算并绘制各工序每天投入工作量（单位：人·小时）的多重折线图：x 轴 表示时间，y 轴表示每天投入的工作量，用不同颜色标记不同工序。

计算并绘制各工序每天投入工作量（单位：人·小时）的多重折线图：x 轴 表示时间，y 轴表示每天投入的工作量，用不同颜色标记不同工序。

计算各个序列的工作时间然后对数据进行合并，x轴为data2的index，y轴为各个序列的时间数据并设置标签等。

结果图：

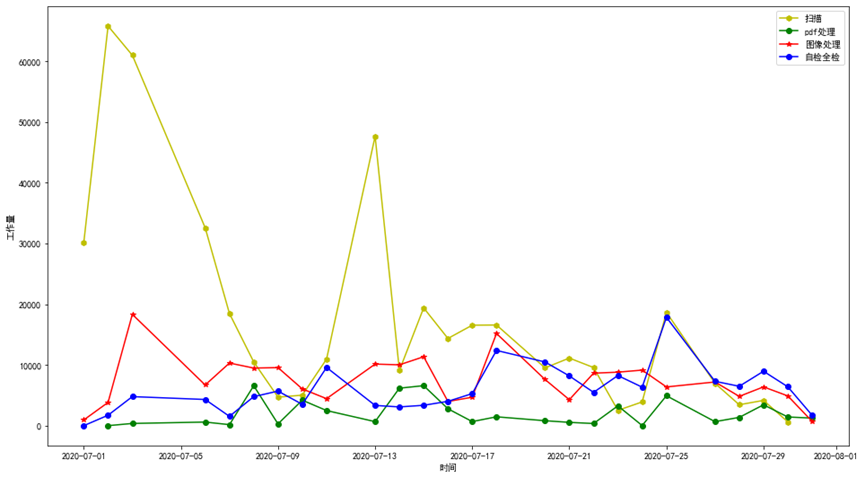从表中可得出各工序每天投入的工作量大致上都在减少，这可能就是人工智能和机械化的结果。

重要代码展示：

import datetime

saowork = saomiao[['day','work']].groupby(by = 'day').sum()
saowork['work']=saowork['work'] /np.timedelta64(1, 'h')
pictwork = pict[['day','work']].groupby(by = 'day').sum()
pictwork['work']=pictwork['work'] /np.timedelta64(1, 'h')
pdfwork = pdf[['day','work']].groupby(by = 'day').sum()
pdfwork['work'] =pdfwork['work'] /np.timedelta64(1, 'h')
zijianwork = zijian[['day','work']].groupby(by = 'day').sum()
zijianwork['work']=zijianwork['work'] /np.timedelta64(1, 'h')

任务 2.3 绘制每天各工序返工案卷数占当天返工案卷总数的百分比堆积面积图：x 轴 表示时间，y 轴表示百分比，用不同颜色标记不同工序。

绘制每天各工序返工案卷数占当天返工案卷总数的百分比堆积面积图：x 轴 表示时间，y 轴表示百分比，用不同颜色标记不同工序积图

统计各个工序返工次数并按日期计数，计算总的返工次数，提取需要的数据并将缺失值填充为0，计算修正后的总返工次数。通过数据计算出工作量设置为y轴，x轴就为时间序列。最后，添加了横轴和纵轴的标签、图例、标题，并展示了图形。

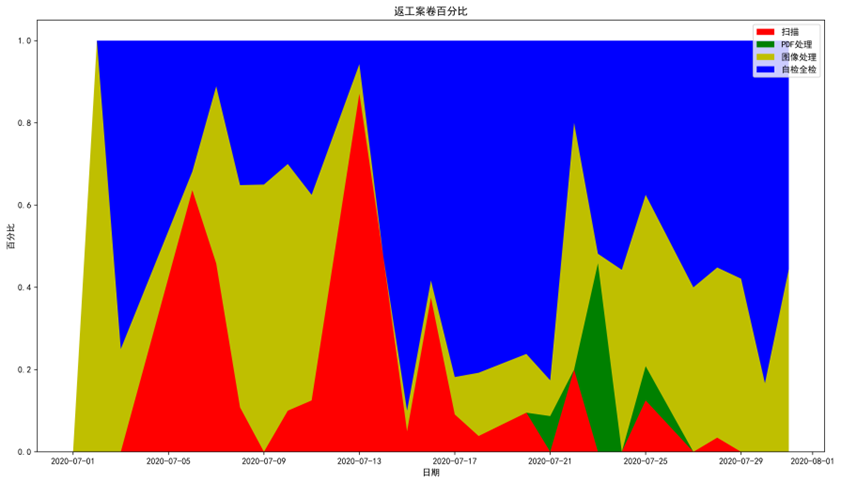
所有从表中可以看出自检全检的返工占比大，第二是图像处理，第三是扫描，第四是PDF。

重要代码如下

saoback = saomiao.loc[saomiao['iNODE_STATUS']==5].day.value_counts()
pictback = pict.loc[pict['iNODE_STATUS']==5].day.value_counts()
pdfback = pdf.loc[pdf['iNODE_STATUS']==5].day.value_counts()
zijianback =zijian.loc[zijian['iNODE_STATUS']==5].day.value_counts()
data3 = pd.concat([saoback,pdfback,pictback,zijianback],axis=1,join='outer')
data3.columns =['saoback','pdfback','pictback','zijianback']

data3['sum'] =data3['saoback']+data3['pdfback']+data3['pictback']+data3['zijianback']

dcd = data1[['saodata']]
data3 = pd.concat([data3,dcd],axis=1,join='outer')[['saoback','pdfback','pictback','zijianback']]
data3 = data3.fillna(0)
data3['sum'] =data3['saoback']+data3['pdfback']+data3['pictback']+data3['zijianback']

任务 2.4 对图像处理工序，汇总每个操作人员返工案卷数，计算其占该工序返工案卷 总数的百分比，并按百分比进行排序，绘制饼图，其中排名第 10 位及以后的合并成一个扇 区。

汇总每个操作人员返工案卷数，计算其占该工序返工案卷 总数的百分比，并按百分比进行排序

首先统计了图像处理返工次数，并按照iUSER_ID进行计数，将结果存储在pictcheck0中。接着，将pictcheck0转换为NumPy数组。然后，对索引为10、11、12的元素进行相加，并将结果赋值给索引为9的元素，用于将多个员工的返工次数合并为一个类别。接下来，只保留前10个元素。然后，导入matplotlib.pyplot库，并创建绘图对象。使用pie函数绘制饼图，通过explode指定各个部分的偏移量，通过labels指定各个部分的标签，通过autopct指定显示百分比的格式。添加标题，并展示图形。最终绘制出了图像员工返工案数的比例图。

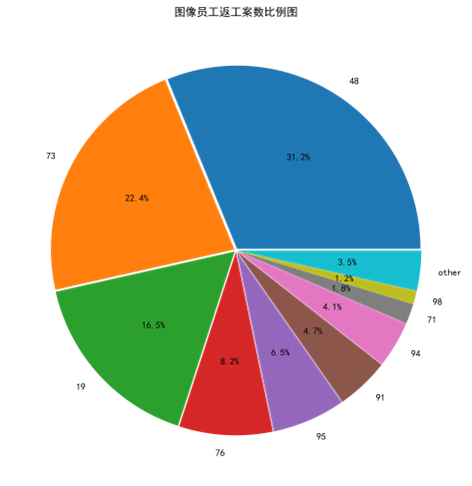
从表中可以看出73、19、48号员工所占比例超过50%效率低，76号员工也有8%需要返工，效率也比较低。

重要代码展示：

pictcheck0 = pict.loc[pict['iNODE_STATUS']==5].iUSER_ID.value_counts()
pictcheck = np.array(pictcheck0)
pictcheck[9] =pictcheck[10]+pictcheck[11]+pictcheck[12]+pictcheck[9]
pictcheck =pictcheck[:10]
import matplotlib.pyplot as plt
explode = [0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01]
label = ['48', '73', '19', '76', '95', '91', '94', '71', '98', 'other']
p = plt.figure(figsize=(16,9),dpi=1080)
plt.pie(pictcheck,explode=explode,labels =label,autopct='%1.1f%%' )
plt.title('图像员工返工案数比例图')
plt.show()

任务 3 领取提交模式分析

由于时间问题任务三只做出了一张图，仅供大家参考

关于领取时间的图片如下：

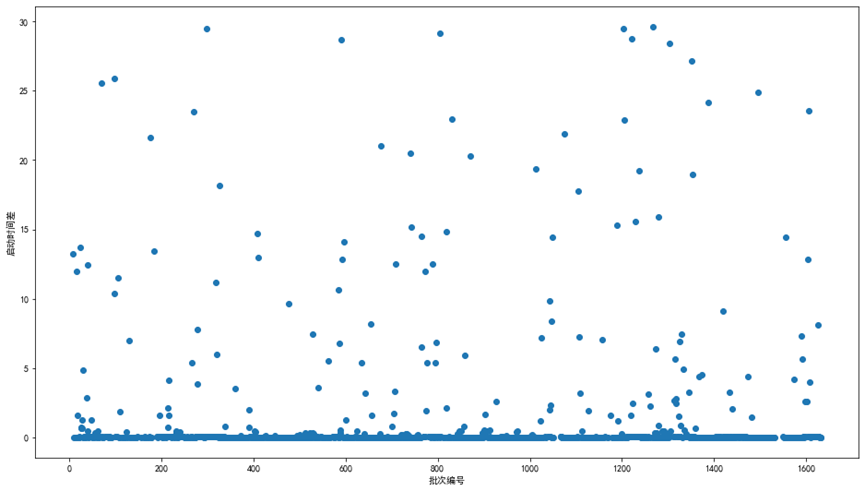
代码如下：

start_time =data[data[['dPROC_TIME']].isnull().T.any()][['dUPDATE_TIME','dPROC_TIME','sBatch_number']]

cmit = start_time[['dUPDATE_TIME','sBatch_number']].groupby(by = 'sBatch_number').max()-start_time[['dUPDATE_TIME','sBatch_number']].groupby(by = 'sBatch_number').min()
cmit['dUPDATE_TIME']=cmit['dUPDATE_TIME'] /np.timedelta64(1, 'm')
cmit = cmit[cmit['dUPDATE_TIME'] < 30.0]
plt.figure(figsize=(16,9))
plt.scatter(cmit.index,cmit['dUPDATE_TIME'])
plt.xlabel('批次编号')
plt.ylabel('启动时间差')
plt.show()