Codeforces Round 920 (Div. 3)补题

Square（Problem - A - Codeforces）

题目大意：给出四点坐标，求正方形面积。

思路：排序根据点的关系求出边长，进而求面积。

#include<bits/stdc++.h>
using namespace std;
bool cmp(pair<int,int>a,pair<int,int>b)
{
	if(a.first!=b.first) return a.first<b.first;
	else return a.second<b.second;
}
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		vector<pair<int,int>>p;
		for(int i=1;i<=4;i++)
		{
			int a,b;
			scanf("%d%d",&a,&b);
			p.push_back({a,b});
		}
		sort(p.begin(),p.end(),cmp);
		int a=p[1].second-p[0].second;
		cout<<a*a<<endl;
	}
}

Arranging Cats（Problem - B - Codeforces）

题目大意：现有两个同长字符串，都只含0和1，我们可以对s1进行操作，每次能进行以下3个操作之一：1.交换其中任意两个字母，2.将其中一个0变成1，3.将其中一个1变成0。问使s1==s2，最少需要操作多少次。

思路：内部肯定先互相移一移配平，然后对于还相差的部分补一补，那么实际上就是统计出两个字串的1的个数，答案就是最大值。另外，如果两个字符串完全相同，那么自然没有讨论的必要，直接输出0即可。

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n;
		scanf("%d",&n);
		string s1,s2;
		cin>>s1;
		cin>>s2;
		int x=0,y=0,o=0;
		for(int i=0;i<n;i++)
		{
			if(s1[i]==s2[i]) o++;
			else if(s1[i]=='1') x++;
			else y++;
		}
		if(o==n) printf("0\n");
		else
		{	
			int ans=max(x,y);
			printf("%d\n",ans);
		}
	}
}

Sending Messages（Problem - C - Codeforces）

题目大意：有n条消息需要发，每条消息只能在指定的时刻发送，每过单位时间，手机电量减少a,如果关机再开始手机电量减少b，可以在开机的同时发消息，现在有f格电量，问能否将所有消息都发出去。

思路：关机时刻是不耗电的，从m1时刻到m2时刻，如果一直开机，那么耗电为(m2-m1)*a，如果m1发完就关机，m2时再开机耗电则为b,故而我们只用循环访问发消息的时刻，一旦电耗空但消息还没发完就判否，另外是先判电量再发消息。

#include<bits/stdc++.h>
using namespace std;
#define int long long
int m[200010];
signed main()
{
	int t;
	scanf("%lld",&t);
	while(t--)
	{
		int n,f,a,b;
		scanf("%lld%lld%lld%lld",&n,&f,&a,&b);
		for(int i=1;i<=n;i++) scanf("%lld",&m[i]);
		int s=0,i;
		int flag=1;
		for(i=1;i<=n;i++)
		{
			int d=m[i]-s;
			int mi=min(d*a,b);
			f -= mi;
			if(f<=0) 
			{
				flag=0;
				break;
			}
			s=m[i];
		}
		if(flag) printf("YES\n");
		else printf("NO\n");
	}
}

Very Different Array（Problem - D - Codeforces）

题目大意：现有一个n长数组a[]，和一个m长数组b[],m>=n，要从b中挑若干个元素形成c[],使得abs(a[i]-c[i])的和最大，问最大的和是多少。

思路：这是一个贪心问题，主要就是找出贪心的策略，我们先将a[],b[]排序：

如图情况，我们可以发现i处的最值可能在选b[l]或者b[r]的时候产生，但是，如果选b[l]实际上a[j]与它配对产生的差值最大。我们统一来看，此时的数组中能产生的最大差值，要么是abs(a[j]-b[l])要么是abs(a[i]-b[r])，我们每次挑出一个差值最大的，那么每步都是当前能产生的最大的，那么结果也一定是最大的。

#include<bits/stdc++.h>
using namespace std;
#define int long long
int a[200010],b[200010];
signed main()
{
	int t;
	scanf("%lld",&t);
	while(t--)
	{
		int n,m;
		scanf("%lld%lld",&n,&m);
		for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
		for(int i=1;i<=m;i++) scanf("%lld",&b[i]);
		sort(a+1,a+1+n);
		sort(b+1,b+1+m);
		int ans=0;
		for(int i=1,j=n,x=1,y=m;i<=j;)
		{
			int l=b[x],r=b[y];
			if(abs(a[i]-r)<abs(a[j]-l))
			{
				ans += abs(l-a[j]);
				x++,j--;
			}
			else
			{
				ans += abs(r-a[i]);
				i++,y--;
			}
		}
		printf("%lld\n",ans);
	}
}

ps:贪心问题一个很重要的思想就是，要使得每一步都是最优，如果我们同时确定两个元素，实际上没办法使得每一步都最优，因为下面这种情况，如果我们在确定a[i]的时候就确定a[j]与b[i]匹配，显然不是最优的，因为与a[j]最后的匹配显然在后面，那么如果在后面的话，a[j]也不能挑b[i-1]，因为它与a[i+1]产生的效益更大，所以，a[j]是最后被匹配的，那么刚好符合上面的那个思路。我们每次只确定一个最大的出来。

?

Eat the Chip（Problem - E - Codeforces）

题目大意：在一个n*m的棋盘中有两个棋子，给出它们的初始位置和可以进行的移动操作，当一个棋子可以覆盖另一个棋子时，这个棋子胜利，当其中一个棋子碰到边界时，游戏平局。

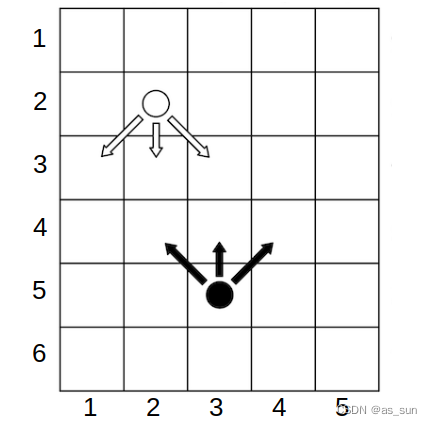
如图为棋子可以进行的移动，当白棋移到最后一行或者黑棋移到第一行时，游戏平局。

思路：首先如果白棋在下，黑棋在上，肯定是平局；如果不是，那么它们肯定在某一行相交，相交的那一行才有可能出现覆盖，因为情况太多，分类讨论肯定不现实，我们来考虑它们在这一行可以达到的左右边界。?

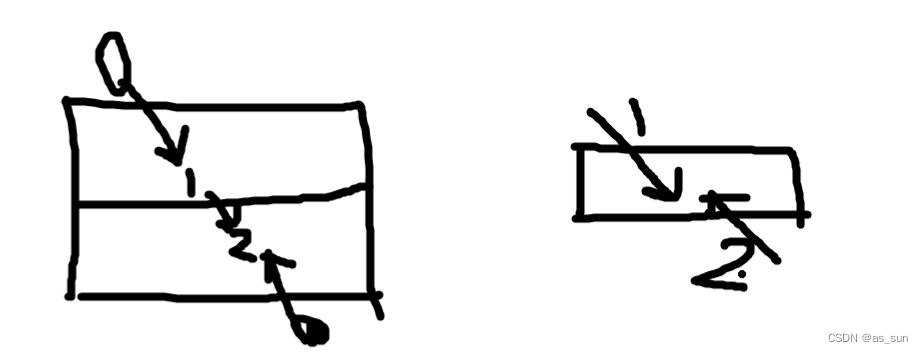
由图可知如果两者之间有偶数行，那么要么平局，要么A胜利，如果是奇数行，要么平局，要么B胜利。那么我们算出它们到这一行的左右边界，如果相隔偶数行，那么就看B能不能移到A的范围之外，如果相隔奇数行，那么就看A能不能移到B的范围之外，至此，题目解决。?

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n,m,ra,ca,rb,cb;
		scanf("%d%d%d%d%d%d",&n,&m,&ra,&ca,&rb,&cb);
		if(ra>=rb) 
		{
			printf("Draw\n");
		}
		else
		{
			int m1=ra+rb,m2;
			if(m1%2)
			{
				m1/=2;
				m2=m1+1;
				int t1=m1-ra+1,t2=rb-m2;
				int la=max(1,ca-t1),ra=min(m,ca+t1),lb=max(1,cb-t2),rb=min(m,cb+t2);
				if(lb<la||rb>ra) printf("Draw\n");
				else printf("Alice\n");
			}
			else
			{
				m1/=2;
				m2=m1;
				int t1=m1-ra,t2=rb-m2;
				int la=max(1,ca-t1),ra=min(m,ca+t1),lb=max(1,cb-t2),rb=min(m,cb+t2);
				if(la<lb||ra>rb) printf("Draw\n");
				else printf("Bob\n");
			}
		}
	}
}

Sum of Progression（Problem - F - Codeforces）

题目大意：现有一个n长数组和q个询问，每个询问给出s,d,k三个值，要求出：

思路：这个用到的数组部分虽然是跳跃的，但是跳跃的区间是一定的，所以我们可以根据d的不同，预处理出来不同的前缀和，我们要使前缀和与结果联系起来：

所以我们只需要预处理两个前缀和即可。但是要考虑一点，我们对于每个d都要预处理一个前缀和，显然是一个嵌套循环，那么预处理的d的范围就要考虑一下，否则就会在预处理的时候超时。大约k取到sqrt(n)就差不多了,这个值差不多只有316左右，上取整就是317，这样差不多就不会超时，另外需要暴力的部分也不会太大。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=100010;
int p1[350][N],p2[350][N];
int a[N];
signed main()
{
	int t;
	scanf("%lld",&t);
	while(t--)
	{
		int n,q;
		scanf("%lld%lld",&n,&q);
		for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
		int l=(int)ceil(sqrt(n));
		for(int k=1;k<=l;k++)
		{
			for(int i=1;i<=n;i++)
			{
				p1[k][i] = (i>=k?p1[k][i-k]:0)+a[i];
				p2[k][i] = (i>=k?p2[k][i-k]:0)+a[i]*i;
			}
		}
		while(q--)
		{
			int s,k,d;
			scanf("%lld%lld%lld",&s,&d,&k);
			int t=s+(k-1)*d;
			if(d<=l)
			{
				int ans = ((p2[d][t]-p2[d][s]+a[s]*s)-(p1[d][t]-p1[d][s]+a[s])*(s-d))/d;
				printf("%lld\n",ans);
			}
			else
			{
				int c=1,ans=0;
				while(s<=t)
				{
					ans += a[s]*c;
					c++;
					s += d;
				}
				printf("%lld\n",ans);
			}
		}
	}
}

ps:比赛和训练不一样，训练是要把所有的题都做出来，顺序就无所谓了，但是比赛不一样，要在规定时间内做出尽可能多的题目，所以一定要讲策略，一旦卡住就马上跳，后面的题未必写不出来，但是耗在一个题上就很浪费时间。