通信入门系列——傅里叶级数和傅里叶正反变换
本节目录
一、傅里叶级数
1、三角形式的傅里叶级数
2、复指数形式的傅里叶级数
二、傅里叶正变换和傅里叶反变换
1、傅里叶正变换
2、傅里叶反变换
3、傅里叶正反变换区别
本节内容
一、傅里叶级数
1、三角形式的傅里叶级数
假设一个周期信号为x(t),周期为T1,满足x(t+T1)=x(t),其角频率为ω1=2π/T1,如果x(t)满足狄里赫利条件,则x(t)可以表示为:
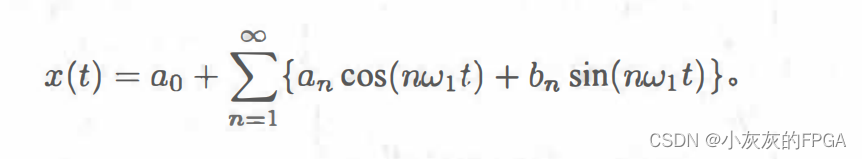
其中狄里赫利条件指的是,一个周期信号满足以下条件:
①在任意一个周期内,有限个间断点;
②在任意一个周期内,有限的极大值与极小值;
③在任意一个周期内,绝对值可积。
a0,an,bn的表达式:
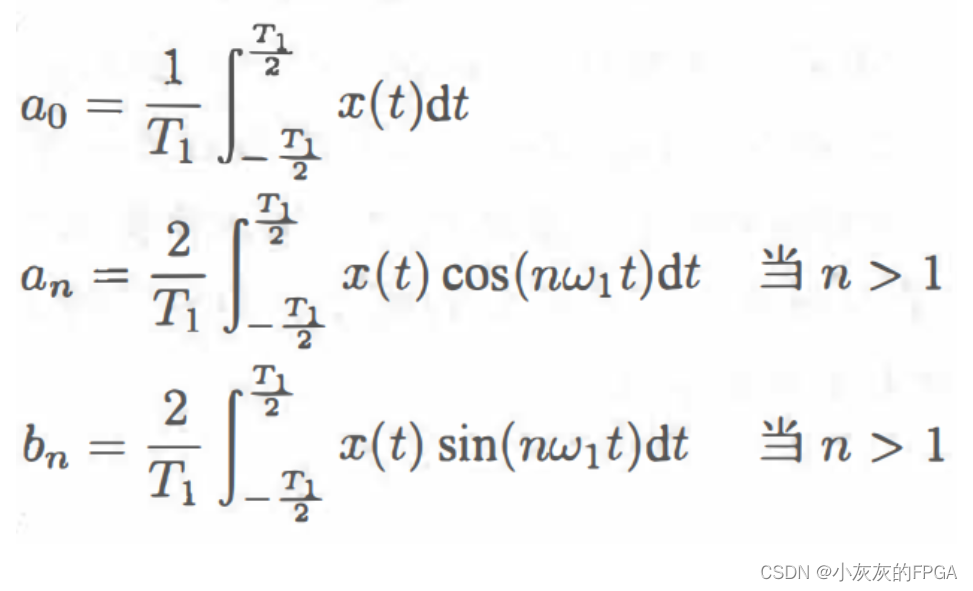
2、复指数形式的傅里叶级数
将欧拉公式代入三角形式的傅里叶级数的公式:
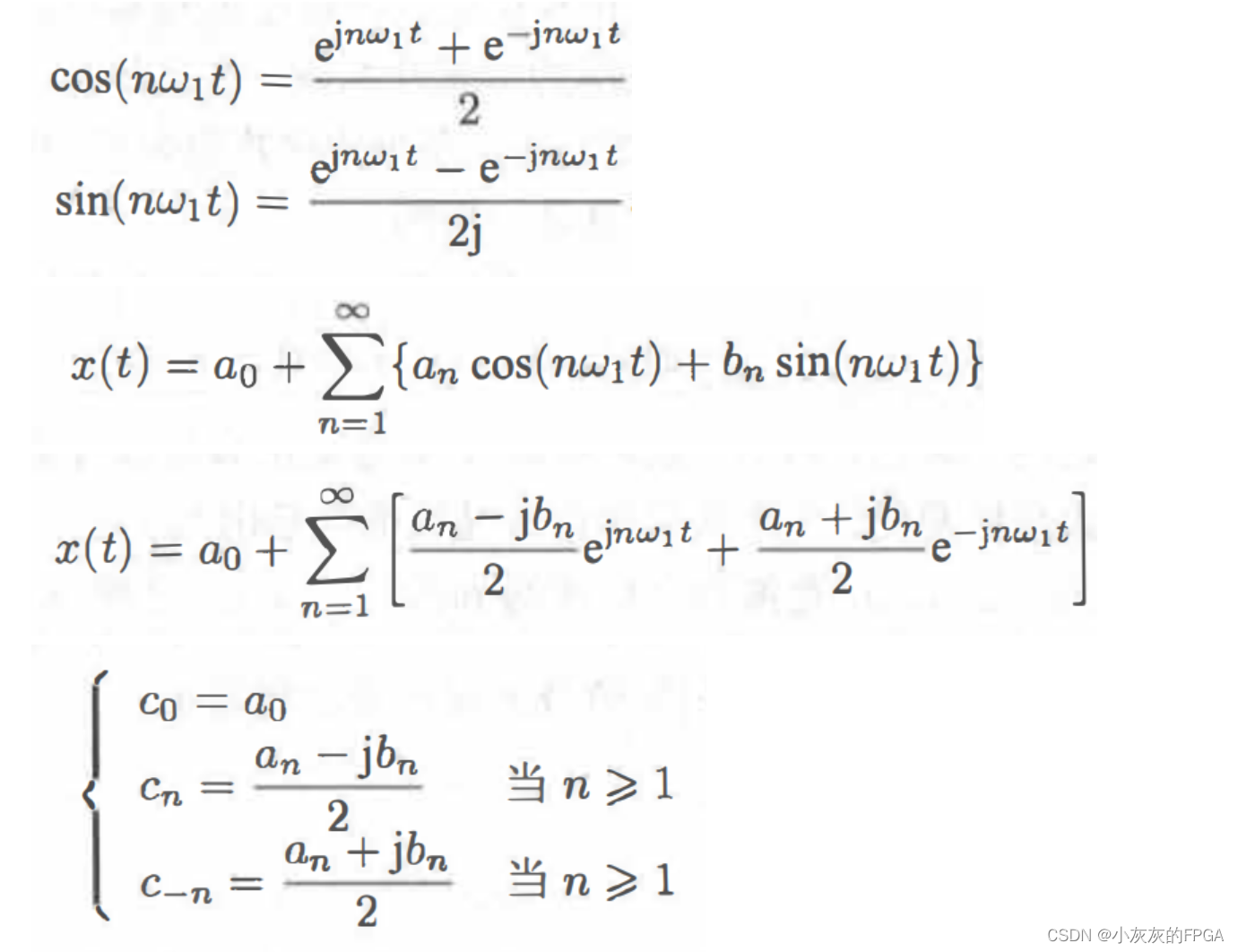
cn称作离散频谱,复指数形式的傅里叶级数如下:
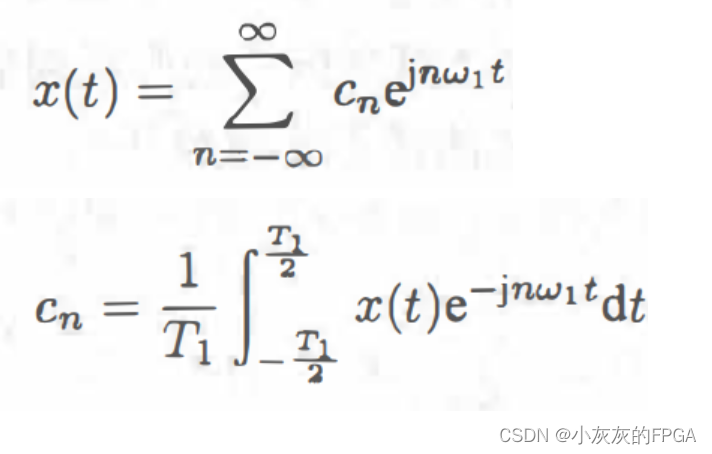
如何理解复指数中的负频率?
负频率是因为复指数造成的,因为欧拉公式,一个正弦信号可以表示为复指数时会出现一个正的频率和一个负的频率,正频率和负频率之间存在对偶关系,正负频率的傅里叶系数,实部相等,虚部相反,通俗讲也就是,幅度相等,相位相反的一对共轭复数。
在通信上,将基带信号调制到载波频率上时,用一个载波信号cos(ωct)去乘以被调制信号cos(ω1t),那么cos(ωct)×cos(ω1t)=1/2×{cos[(ωc-ω1)t]+cos[(ωc+ω1)t]}。其实也就是所谓的频谱搬移,就是将基带信号搬移到载波频率上,一个频率ω1的信号经过载波频率ωc的信号调制后出现了ωc-ω1和ωc+ω1两个频率,其中ωc-ω1是搬移到负频率得到的,ωc+ω1是搬移到正频率得到的,这种情况称为双边频谱,关于载波频率ωc对称。
二、傅里叶正变换和傅里叶反变换
1、傅里叶正变换
傅里叶正变换,将时域信号变换为频域信号,其公式可以表示为:
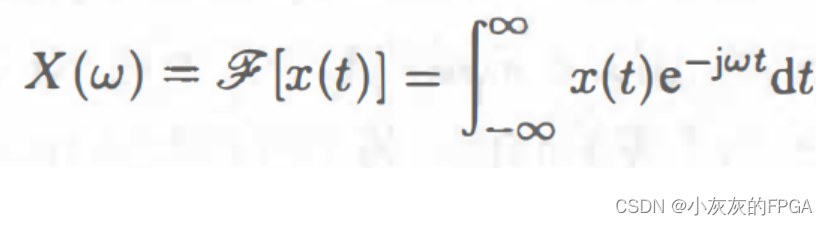
如何推导傅里叶正变换?
由周期信号的复指数形式的傅里叶级数开始,一个周期为T1,角频率ω1为2π/T1的周期信号,其复指数傅里叶级数为:
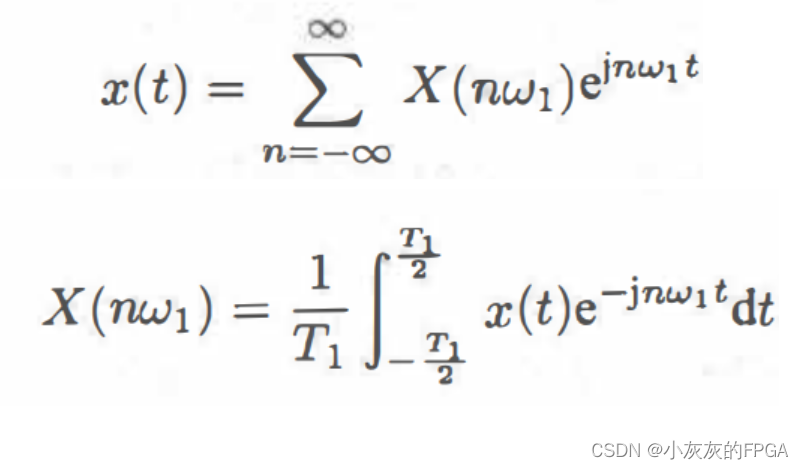
将非周期信号,认为是周期无线大的周期信号,也就是T1→∞,谱线间距2π/T1→0,离散频谱就变成了连续频谱。
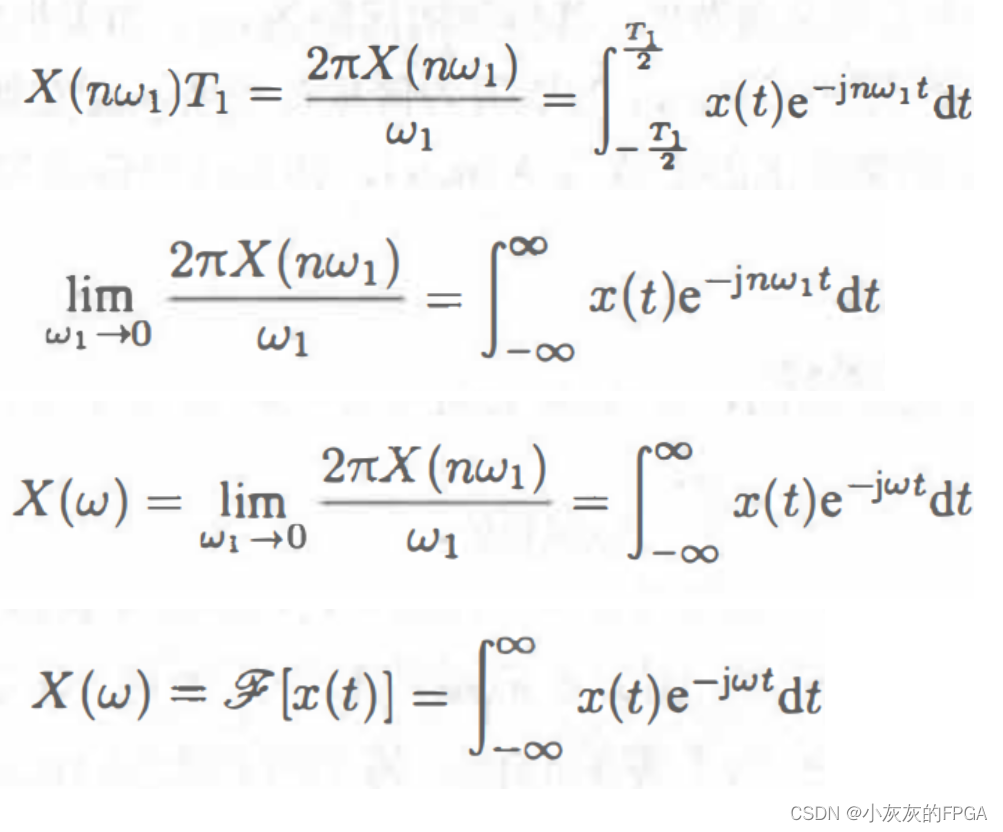
2、傅里叶反变换
傅里叶反变换,将频域信号变换为时域信号,其公式可以表示为:
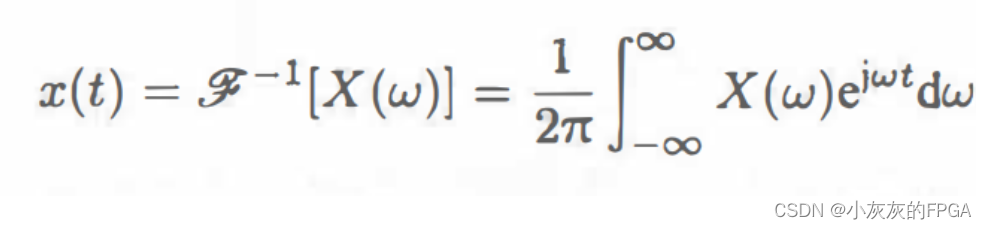
如何推导傅里叶反变换?
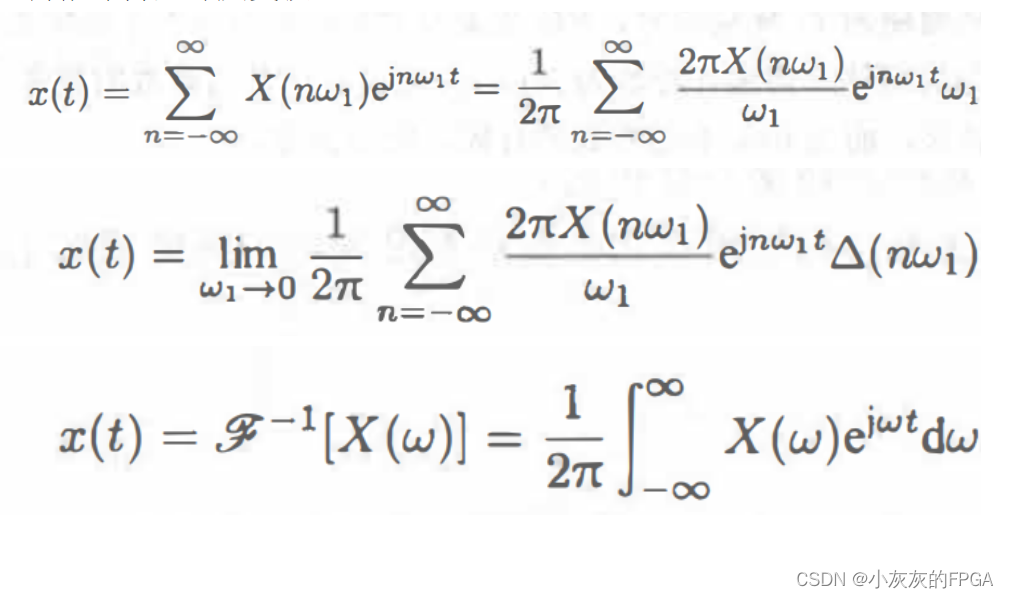
3、傅里叶正反变换区别
傅里叶正变换积分内的指数上有一个负号,而傅里叶反变换积分内的指数是正号。傅里叶正变换是信号与基函数e^(jωt)做内积,复数做内积需要取共轭,故有一个负号。而傅里叶反变换,是用基函数合成原来的信号,所以不存在负号。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 为布偶猫精心挑选的三款主食冻干,K9、sc、希喂深度解析对比
- zookerper入门
- Java Stack类
- 系列五(实战)、发送 & 接收同步消息(Java操作RocketMQ)
- NLP论文阅读记录 - 2022 sota | 校准序列似然改善条件语言生成
- 【力扣每日一题】力扣2788用分隔符拆分字符串
- 【无标题】
- 手把手写深度学习(1):WebVid-10M数据清洗之文字/水印检测清洗-复现Stable Video Diffusion论文
- SQL注入--一起学习吧之安全测试
- MyBatis的运行原理!!!