《算法设计与分析》复习
复习参考:
《算法设计与分析基础》潘彦译
【北大公开课】 算法设计与分析
【算法设计与分析】期末考试知识总结(知识超浓缩版)
《算法分析与设计》复习笔记
【期末知识点整理】算法设计与分析
算法设计与分析——算法复杂性分析
一、基础知识
-
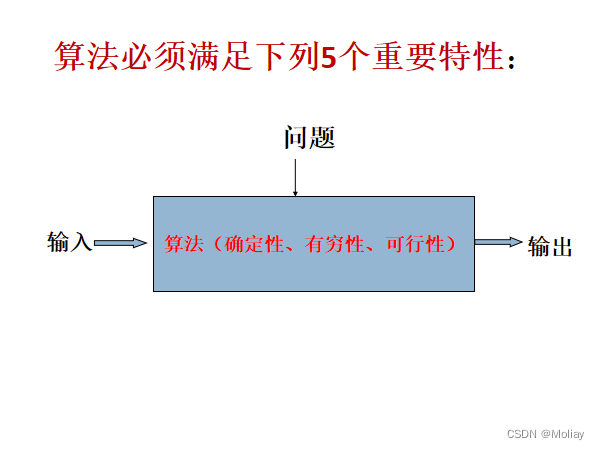
算法是一系列解决问题的明确指令。换言之,对于符合一定规范的输入,能够在有效时间内获得要求的输出。
-
算法:具有输入、输出、确定性、有限性。
-
程序(算法+数据结构=程序):具有输入、输出、确定性(注意:程序可以不满足有限性,如操作系统是在无限循环中执行的程序)。
-
衡量算法好坏的方法:正确性(有限时间正确结果)、简明性、效率(时间、空间)、最优性
-
算法的基本特征
- 有限性:一个算法必须总是(对任何合法的输入值)在执行有限步之后结束
- 确定性:算法中的每一条指令必须有确切的含义,不产生二义性
- 可行性:算法中的每一条运算都必须是足够基本的,原则上能够精确的执行
- 输入性:一个算法有零个或多个输入
- 输出性:一个算法有一个或多个输出
-
背包问题
- 蛮力法
优点:简单明了
缺点:时间复杂度高,对于大规模问题不适用。 - 回溯法
优点:时间复杂度较低,可以找到最优解
缺点:需要额外的空间来存储递归过程中的解。 - 动态规划
优点:时间复杂度较低,可以处理大规模问题
缺点:需要额外的空间来存储子问题的解 - 贪心法
该问题不具备贪心选择性质,通过局部最优,无法达到全局最优,故不能得到正确的解
- 蛮力法
二、算法效率分析基础
-
渐进意义下的符号:
-
Ο,表示渐进上界(tightness unknown),小于等于的意思,近似复杂度。
-
Ω,表示渐进下界(tightness unknown),大于等于的意思,近似复杂度。
-
Θ,表示确界,既是上界也是下界(tight),就是相等,准确的复杂度。

-
-
常见的时间复杂度大小关系:O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

-
分析非递归算法效率的通用方案
- 决定用哪个(哪些)参数表示输入规模
- 找出算法的基本操作(作为一个规律,它总是位于算法的最内层循环中)
- 检查基本操作的执行次数是否只依赖于输入规模。若它还依赖于一些其他的特性,则最差效率、平均效率以及最优效率(如有必要)需要分别研究
- 建立一个算法基本操作执行次数的求和表达式
(分析非递归的基本操作次数时,某些情况下需要建立一个递推关系,而不是一个求和表达式;在分析递归时递推关系更为常见) - 利用求和运算的标准公式和法则来建立一个操作次数的闭合公式,或者至少确定它的增长次数。

-
分析递归算法时间效率的通用方案
- 决定用哪个(哪些)参数作为输入规模的度量标准
- 找出算法的基本操作
- 检查一下,对于相同规模的不同输入,基本操作的执行次数是否可能不同。若有该可能,则必须对最差效率、平均效率以及最优效率做单独研究。
- 对于算法基本操作的执行次数,建立一个递推关系以及相应的初始条件。
- 解这个递推式,或者至少确定它的解的增长次数
主定理法

对于递归式T(n) = aT(n/b) + f(n),比较根节点代价之和f(n)和叶子节点代价之和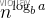 的大小
的大小

也就是在比较合并成本和叶子成本,究竟谁更大。粗略的理解如下:
① f(n)多项式意义大于 ,不止渐进大于且相差n^ε,所以总体代价以f(n)为主;(这里忽略了对正则条件的理解,感觉不影响使用,想了解深层原理可以看一下课本)
② f(n)与 等阶,最后的结果要再乘以logn
③ f(n)多项式意义小于,不止渐进小于且相差n^ε,所以总体代价为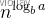
这三种情况画在线段上如下图所示,所以中间哪些无法覆盖的部分就是这个定理无法涵盖的情况。具体的讲解还是可以看看那个北航老师的视频。


注意:要使用第三种情况,需要满足条件验证,其中c<1


- 函数的阶具有传递性
三、蛮力法
【概述】蛮力法是一种简单、暴力、直接解决问题的方法,通常直接基于问题的描述和所涉及的概念定义,依赖计算机的计算速度直接求解。
【步骤】搜索所有的解空间、搜索所有的路径、直接计算、模拟和仿真。
【理解】有的暴力枚举即可,有的直接模拟即可。
字符串匹配
时间复杂度为O(nm),其中n是主字符串的长度,m是模式字符串的长度
空复O(1)
最近对问题
暴力法 时复Θ(n2)
最近对问题的一个最重要的应用是统计学中的聚类分析。(填空)
凸包问题
- 对于平面上的一个点的有限集合,如果以集合中任意两点P和Q为端点的线段上的点都属于该集合,则称该集合是凸集合
- 凸包
(直观版)对于平面上n个点的集合,它的凸包就是包含所有这些点(在内部或边界上)的最小凸多边形
(正式版)一个点集合S的凸包是包含S的最小凸集合(最小即S的凸包一定是所有 包含S的凸集合 的子集) - 凸包问题
是为一个有n个点的集合构造凸包的问题。为了解决该问题,需要找出极点(作为这个集合的凸多边形的顶点)(填空) - 解决方法:
- 暴力法 时复O(n3)
穷举查找
旅行商问题
找出一条n个给定城市间的最短路径,其中要求回到出发的城市&每个城市都只访问一次。则该问题可以理解为求一个图的最短哈密顿回路问题。
哈密顿图(哈密尔顿图)(英语:Hamiltonian graph,或Traceable graph)是一个无向图,由天文学家哈密顿提出,由指定的起点前往指定的终点,途中经过所有其他节点且只经过一次。在图论中是指含有哈密顿回路的图,闭合的哈密顿路径称作哈密顿回路(Hamiltonian cycle),含有图中所有顶点的路径称作哈密顿路径(Hamiltonian path)
- 蛮力法求解哈密顿回路在最坏情况下需要考察所有顶点的排列对象,其时间复杂性为O(n!)
背包问题
时复 O(2n)
分配问题
有n个任务分配给n个人执行,一个任务对应一个人。给出对于每个任务,这n个人完成分别的成本。求总成本最小的分配方案。
- 蛮力法求解任务分配问题需要求解的排列数是n!
深度优先查找和广度优先查找
邻接矩阵O(n2)
邻接表O(n+e)
空间复杂度相同,都是O(n)
四、减治法
使问题变成与原问题相同的但是规模更小的子问题,解决这个子问题,延伸子问题的解决方法,从而得到原问题的解决方案
- 种类(期末可能考该题,填空):
- 减一个常量(如插排、拓排、全排列、求子集、dfs、bfs、堆排序)
- 减一个常量因子(如二分查找、快速幂、俄罗斯乘法、约瑟夫斯、假币问题)
- 减可变规模(如欧几里得算法、nim游戏、快排划分)
插入排序
减一
拓扑排序
删去入度为0的点
减常因子算法
折半查找
假币问题
在n枚外观相同的硬币中,有一枚是假币。在一架天平上,可以比较任意两组硬币,即通过观察天平是向右倾还是左倾或中间,课判断哪组更重。假设假币较轻。
进一步优化:增加堆数
俄式乘法
约瑟夫问题
减可变规模算法
计算中值和选择问题
插值查找
折半的优化
where:有序表
- 折半查找vs插值查找
- 对于较小的文件,折半查找可能更好
- 对于更大的文件和那些比较开销较大或访问成本较高的应用,插值查找更值得考虑
五、分治法
【概述】对于一个规模为n的问题,若该问题可以容易的解决(比如n的规模较小)则直接解决,否则将其分解为k个规模较小的子问题(即具有最优子结构性质),这些子问题互相独立且与原问题形式相同,递归地解决这些子问题,然后将各子问题的解合并得到原问题的解。
- 分治法的设计思想是把一个难以直接解决的大问题分割为较小的子问题,分别解决子问题,最后把子问题的解组合起来形成原问题的解,这要求原问题和子问题的问题规模不同,问题性质相同(选择)
【步骤】将大问题分解为若干个子问题、求解子问题、合并子问题的结果得到最终解。
分治法的工作方案:
(1)把一个问题划分为同一类型的若干子问题,子问题最好规模相同(平衡)
(2)对这些子问题求解(一般使用递归),但问题规模 足够小时,也会利用另一个算法)(可独立求解)
(3)有必要的的话,合并这些子问题的解,以得到原始问题的答案。
【理解】分而治之,逐个击破。 - 分治法的使用条件
(1)问题缩小到一定的规模(子问题)时易解决
(2)原问题与分解后的子问题同类(即该问题具有最优子结构性质)
(3)原问题的解可以由子问题的解合并得到
(4)子问题相互独立,不包含公共问题。、
合并排序(归并排序)
优点:稳定性
缺点:需要线性的额外空间
快速排序
平均性能O(nlogn)
大整数乘法
四次变三次,减少乘法次数
=》通过代数变换,减少a(规约后的子问题个数)
Strassen矩阵乘法
用分治法解最近对问题和凸包问题
最近对问题
1、问题描述
求空间内,最近的两个点(最简单的就是一维问题,然后可以上升为二维的)
2、一维的最近点对的解题思路
同理,先分析是否满足分治法的适用条件:可以把空间分成两部分,求每个小空间的最近距离,但是在合并的时候,交界处比较难处理,但是也算是满足条件
- 分治法求解:
- 分解:用各个点坐标的中位数m 作为分割点,分成两个点集
- 解决:递归调用该算法,分别寻找两个点集上最接近的点对{p1, p2}、{q1, q2}及距离d1,d2
- 合并:整个点集的最近点对或者是{p1, p2},或者是 {q1,q2},或者是某个{p3,q3},其中p3和q3分属两个点集(整个情况在合并的时候要仔细分析)
合并策略:如果说两个点集的交界处有更近的点,那找到这俩个点,需要扫描的范围其实不会超过,两边的最近距离d的二倍,画个图如下所示,这2d的范围中,最多只可能会有4个点,如果说p1和p2之间还有其他的的点,那就会构成比d更近的距离了

所以,合并的时候,我们需要在从分割点 出发 分别往左右扫描扫描到d的距离,看看是否会出现更近的情况就可以啦
3、二维最近点对问题的解题思路
有了一维的基础,再考虑二维的问题就好理解多了,直接来分治法求解过程:
(1)预处理:将点集P中的点,按照X Y坐标从小到大顺序排列
(2)分解:计算x坐标中位数m,选择一条垂线L:x=m,将点集P分成左右两部分PL和PR,分解到最后的递归出口,剩1~3个点时,就可以直接计算了
(3)解决:递归调用该算法,分别找PL和PR中的最近点对及距离,距离分别记为δL, δR,置δ = min(δL, δR)
(4)合并:考察带状区域中的点
① 找出以L为中心线,宽度为2𝛿的带状区域
② 获得带状区域中排序后的点集Y’
③ 对Y’中的每个点,检查其后面的7个点,计算距离并更新最近点对的距离
为啥是7个点呢,看以下分析:
其实跟一维一个道理,再这个带状区域中,最多只可能存在8个点,如下图,因为如果再想多一个点,就会在L的一边存在比δ更进的距离,所以,只需要分析一个点往后的7个点就足够了
4、时间复杂度分析
递归式为:T(n) = 2T(n/2)+f(n)
f(n) = O(n)
得出最后时间复杂度:==> T(n) = O(nlgn)
凸包问题
解凸包问题的分治算法也称为快包(因为它的操作和快排操作类似)
总体时间复杂度O(nlogn),最差效率Θ(n2)
六、变治法(可能考变治的应用)
预排序
若列表是有序的,许多关于列表的问题更容易求解
- 思想应用:
- 检验数组中元素的唯一性
- 模式计算
在给定的数字列表中最经常出现的一个数值称为模式 - 查找问题
- 最近对问题 和 凸包问题的 分治算法都采用了预排序
高斯消去法
(联想 线代中的初等变换来实现消元)
- 第一阶段:前向消去(化为行阶梯)
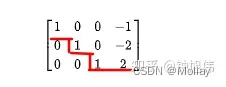
A[i,i]可能会非常小
=>A[j,i]/A[i,i]会很大
=>A[j,k]的新值会因为舍入误差而歪曲
为了避免该问题,每次都去找第i列系数的绝对值最大的行,再把它作为第i次迭代的基点。
这种修改,称为部分选主元法。它保证比例因子的绝对值不会大于1
- 第二阶段:反向替换(化为类似行最简)
平衡查找树
平衡查找树
AVL树(平衡二叉树)
在AVL树中,任一节点对应的两棵子树的最大高度差为1
2-3tree
插入 时复(logn)
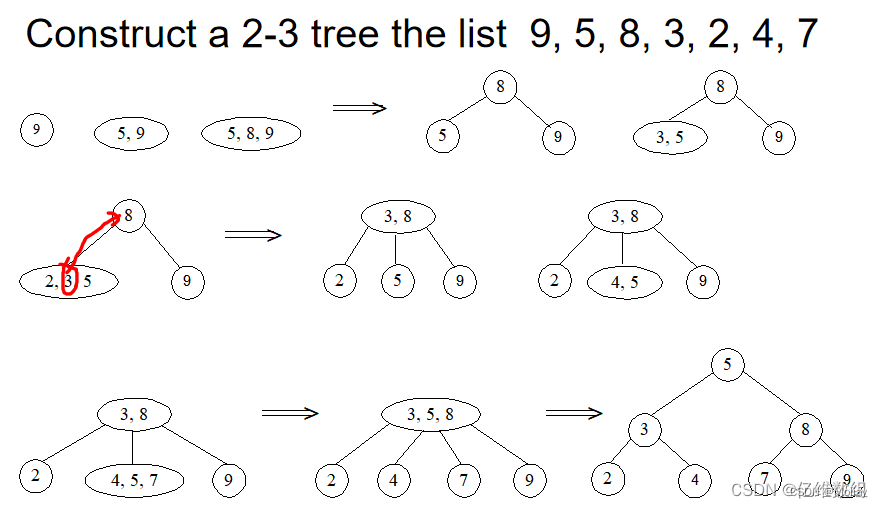
跟avl树的插入方式一样,只不过每一个结点可以容纳1~2个结点,当结点数量到达三个时,就会“分裂”成一个小avl树
堆和堆排序
堆是一棵完全二叉树&每个节点的键都要大于或等于其子女的键(以大根堆为例)
堆排序时复Θ(nlogn),空复O(1)
霍纳法则和二进制幂
- 多项式构成了最重要的一类函数:
- 拥有许多好的特性
- 可用它们来近似计算其他类型的函数
解决多项式问题的一种重要算法是快速傅里叶变换,基本思想是用多项式在某些特定点上的值来表示该多项式。
霍纳法则
时复O(n)
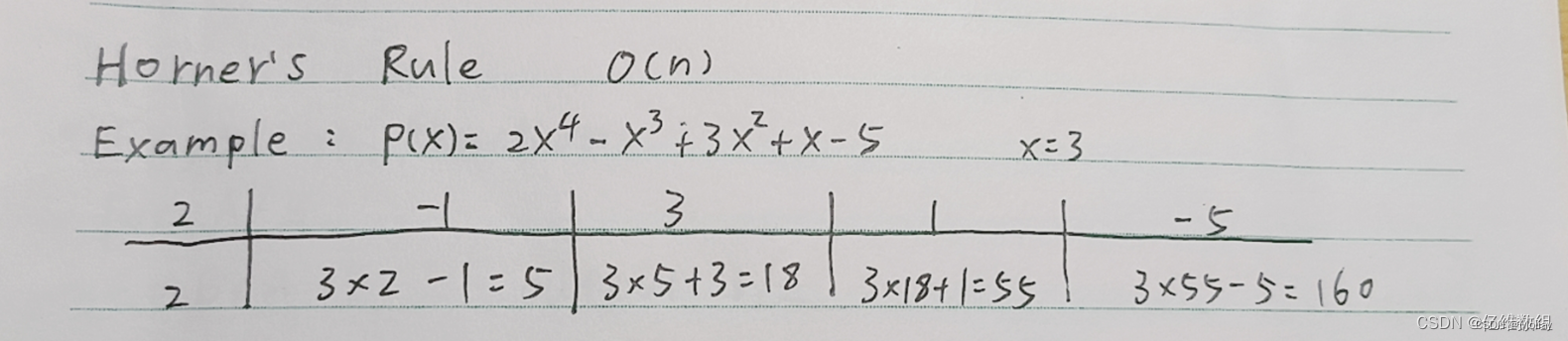
二进制幂
用霍纳法则计算an,时复O(n)

用从左至右二进制幂算法计算a13,n=13=11012(期末可能考该类题)

问题化简
求最小公倍数
计算图中的路径数量
优化问题的化简
线性规划
简化为图问题
七、时空权衡
作为一种算法设计技术,空间换时间 要比 时间换空间 更为普遍
- 空间换时间技术有两种主要类型:
- 输入增强
对 问题输入的部分或全部 做预处理,再把获得的额外信息进行存储,来加速后面问题的解决。
例如计数排序 - 预构造
使用额外的空间来实现更快和(或)更方便的数据存储。
例如散列、B树
- 输入增强
(比较)计数排序
- 优点:减少数据的移动
- 时复O(n2)
- 应用:外部磁盘存取
- 分布计数排序
- 对排序的关键字有要求:关键字要连续&有上界和下界
- 时复O(n)
字符串匹配中的输入增强技术
字符匹配蛮力算法最差性能是O(nm),其中m是模式串的长度,n是字符串长度。
- 用于字符串匹配的Horspool算法可以看作是Boyer-Moore算法的一个简化版本。
- 相同点
- 都以输入增强思想为基础,且从右向左比较模式中的字符
- 都用同样的 坏符号移动表
- 不同点
- Boyer-Moore算法害使用了第二个表,称为好后缀移动表
- 相同点
Horspool算法
最差效率O(nm)
平均情况下时复O(n)

Boyer-Moore算法
时复O(n)
散列表
B树
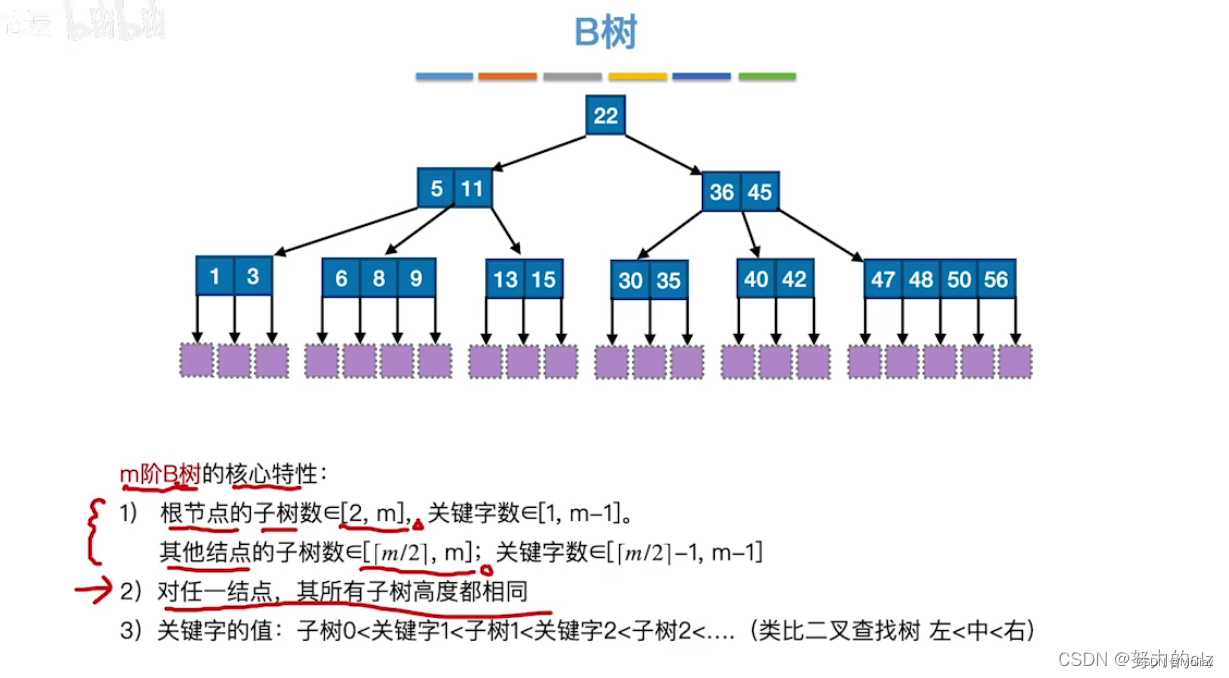
B树进行查找、插入和删除的时间效率都是O(logn)
八、动态规划
- 动态规划的适用范围
- 分解子问题,子问题重叠
- 具有最优子结构的性质(即 大问题的最优解包含小问题的最优解)
- 求解的方式是自底向上,先求小问题
- (选择)动态规划算法的基本要素是最优子结构和重叠子问题
【概述】动态规划是一种解决多阶段决策问题的优化方法,把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解。能用动态规划法的问题一般具有3个性质:最优子结构,无后效性,有重叠子问题。
【步骤】分析最优解的性质,递归的定义最优解;以自底向上或自顶向下的记忆化方式计算出最优值;根据计算最优值时得到的信息,构造问题的最优解。
【理解】自底向上的构建过程。
- 动态规划VS分治:
- 相同点:原问题分解成子问题,先求解子问题,从中得到原问题的解
- 不同点:
- 1.动态规划中的子问题不是相互独立的,分治法中的子问题相互独立
- 2.动态规划碰到相同的子问题只需要查询答案,而分治法会重新求解,效率更低
- 动态规划VS贪心:
- 相同点:都是求解最优化问题,都有最优子结构性质(原问题的最优解包含子问题最优解)
- 不同点:
- 1.动态规划是自底向上,贪心是自顶向下
- 2.动态规划依赖于各子问题的解,只有在解出相关子问题之后,才能做出选择,而贪心法不依赖于子问题的解,仅在当前状态下做出最好选择
三个基本例子
币值最大化

找零问题

硬币收集问题


背包问题和记忆功能
背包问题

记忆化
最优二叉查找树(考试重点)
最优的(即平均比较次数最少的) 二分检索树

复杂性估计:
时间复杂性:T(n)=O(n3)
空间复杂性: S(n)=O(n2)
Warshall算法和Floyd算法
Warshall算法——计算有向图的传递闭包
Floyd算法————计算全部的最短路径

九、贪心
活动 安排/选择 问题
结束时间早的优先
排序使得f1≤f2≤…≤fn,从前向后挑选(fi是活动i的结束时间)
时复O(nlogn)

- 贪心法建议通过一系列步骤来构造问题的解,每一步对当前构造的部分解做一个扩展,直到获得问题的完整解为止。该技术的核心在于,所做的每一步选择都必须满足以下条件:
- 可行的(必须满足问题的约束)
- 局部最优
- 不可取消(选择一旦做出,后面步骤中就无法改变了)
- 贪心的证明方法:
- 反证法
- 替换法
- 下界法
- 决策树:
- 回溯法
- 分治法
- 动态规划
- 贪心
零钱问题

十、迭代改进
单纯形法

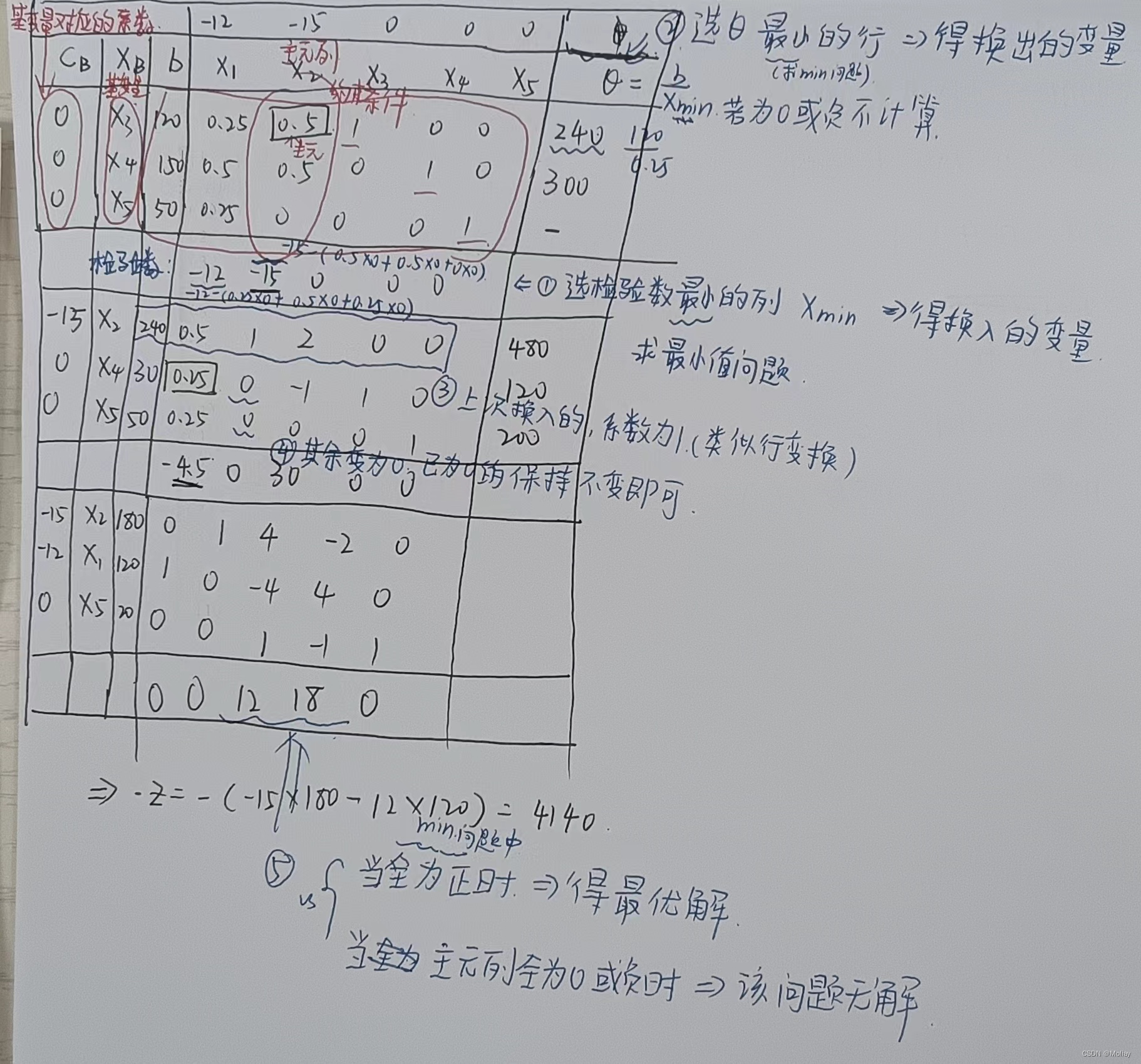
最大流量问题
一个给定网络的可行流是实数值xij对边(i,j)的分配,使得网络满足流量守恒约束和容量约束
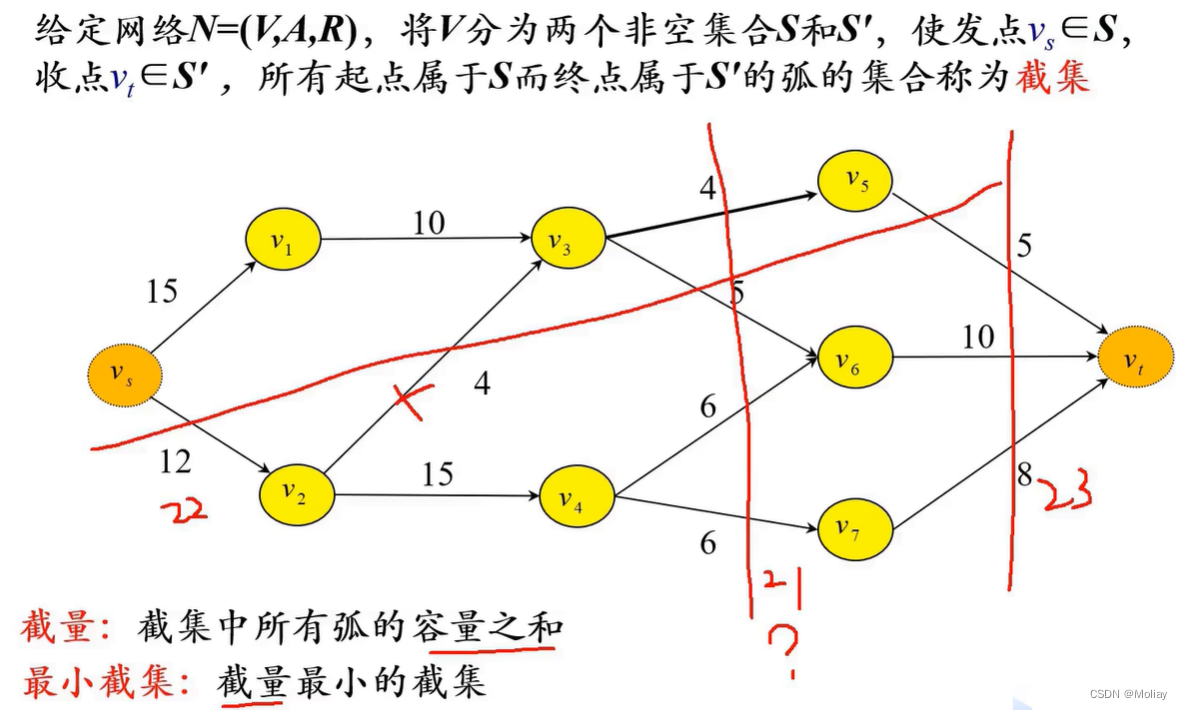
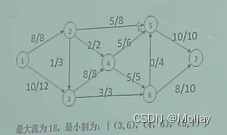
找最小割:正向饱和的点和汇点一同做补集
二分图的最大匹配
- 图的一个匹配:即图中边的子集,其中任两条边都不共一个顶点(是简单路径)
- 最大(基数)匹配:包含 最多匹配边 的匹配
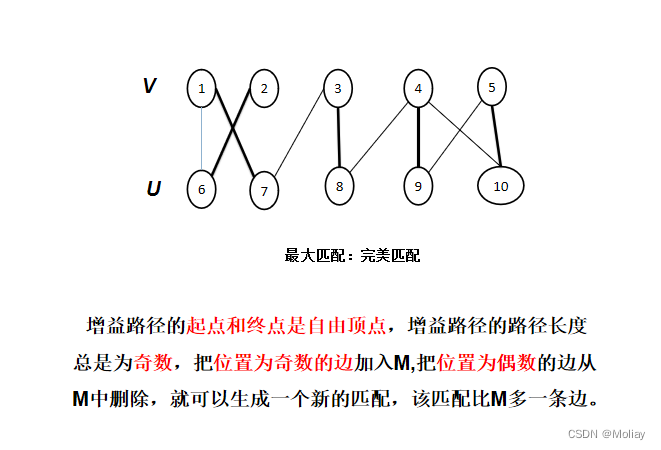
- 完美匹配:一个匹配中,图中的每个顶点都和图中某条边相关联。换言之,匹配了图中的所有顶点。
- 当且仅当M不存在增益路径时,M是最大匹配。
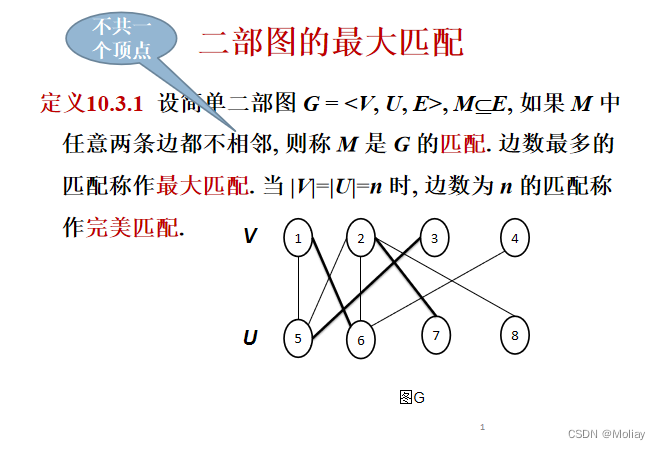
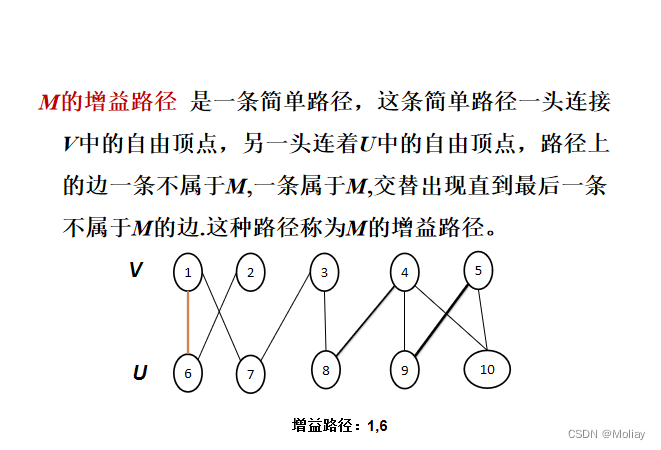
- 对二部图G=<A,B,E>, 匈牙利算法终止时M是G的最
大匹配, 并且算法在 O(min{|A|,|B|}*|E|) 步内终止

十一、回溯与分支限界
- 解空间树:不考虑任何条件,穷举所有情况的树结构(通常是满多叉树,但不尽然,总之列举所有情况就行)
- 搜索空间树:解空间树在解空间树减枝后的空间树
- 当所给的问题是从n个元素组成的集合S中找出满足某种性质的一个子集时,相应的解空间树称为子集树
解空间为子集树的常见问题:
(1)0-1背包问题;
(2)子集和问题;
(3)装载问题;
(4)最大团问题。 - 当所给的问题是从n个元素的排列中找出某种性质的一个排列时,相应的解空间树称为排列树
解空间为排列树的常见问题:
(1)n皇后问题;
(2)旅行商问题(货郎问题)
(3)园排列问题;
(4)电路板排列问题。 - 用回溯法求解图的着色问题的搜索空间是一颗m叉树(选择)


- 回溯法的适用条件:多米诺性质,即k维向量不满足的约束条件,扩张到k+1维仍不满足,可回溯。

最大团问题
- G的点独立集:是G的顶点子集且任何两个顶点间都没有边
- U是G的最大团,则其补图为最大点独立集

分支限界法最坏情况下,可能都不能裁剪下来

图着色问题
n为顶点数,m为颜色种类数

十二、算法分析与问题的计算复杂度
- 对于给定的问题,可能有多种算法。每个算法的时间复杂度不一样,算法的效率越高,占用的时间就越少。
- 问题的计算复杂度是求解这个问题所需要的最少工作量,它是由问题本身结构决定的内在性质,与求解它的算法好坏无关。
- 求解一个问题的最好算法,它的时间复杂度函数应该恰好等于问题的计算复杂度。
- 可以从求解某个问题的算法出发来帮助确定问题的计算复杂度。
- 对于给定的问题,算法的时间复杂度相当于问题的计算复杂度的一个上界。给出一个算法,就得到一个上界。随着算法的不断改进,这个上界不断降低,直到接近问题的计算复杂度。
- 在实践中,上界和下界的改进是同时进行的,当上界和下界的值相等或它们的阶相等时,就得到了问题的计算复杂度。
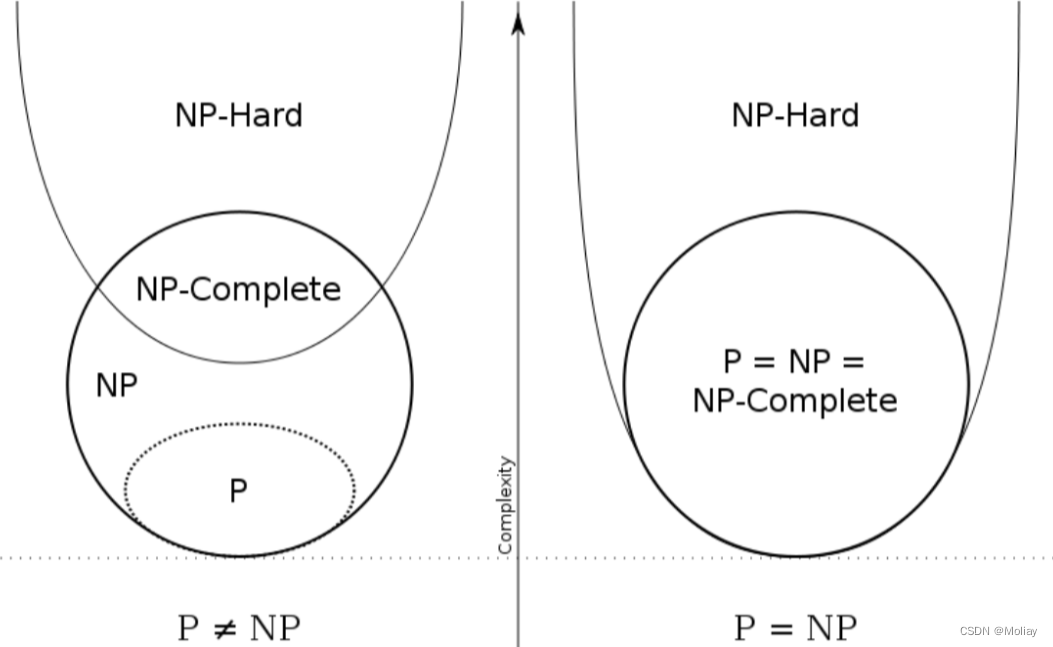
- P类问题是多项式时间内可解的
- NP类问题是多项式时间内可验证
- NPC问题:存在这样一个NP问题,所有的NP问题都可以约化成它。这种问题不只一个,它有很多个,它是一类问题。这一类问题就是NPC 问题。其定义要满足2个条件:
- 它是一个NP问题;
- 所有NP问题都能规约到它。
- NP-hard问题:满足NPC问题定义的第二条而不满足第一条。即所有的NP问题都能约化到它,但是他不一定是一个NP问题。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 华为VRP常见基本命令
- C#实现串口通讯
- Python能做大项目(6)Poetry -- 项目管理的诗和远方之一
- 根据一个现有值,获取其在数组中的索引,上下位置的值
- Android 自动化测试——Monkey测试
- 不会有人上台阶摔倒吧 3476:【例86.1】 上台阶
- 第02章_变量与进制
- 【Python】nn.init.constant_()函数详解和示例
- 用Python做生信分析--环境配置以哦见状
- netty源码:(38)ByteToMessageDecoder类