C语言实现八大排序算法(详解插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序(递归和非递归)、归并排序(递归和非递归)和计数排序)
文章目录
写在前面
本篇文章使用C语言实现了数据结构中常见的八大排序算法,它们分别是插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序和计数排序。在排序算法的实现过程中,每种算法都有其独特的特点和适用场景。插入排序通过逐步构建有序序列来排序,希尔排序则是对插入排序的一种改进,通过缩小增量的方式提高了效率。选择排序通过不断选择未排序部分的最小元素进行交换,而堆排序则利用了二叉堆的性质来实现高效的排序。冒泡排序通过多次遍历数组,将相邻元素进行比较和交换,逐步将最大元素移动到数组末尾。快速排序采用分治策略,通过选择一个基准元素,将数组分为两部分进行递归排序。归并排序则是将数组分为两个子数组,分别排序后再合并,以此达到整体有序的效果。最后,计数排序通过统计元素出现的次数,然后按顺序输出,实现了线性时间复杂度。下面我们将一一详细介绍它们,并给出了完整的实现代码。

1. 直接插入排序
算法思想:直接插入排序是一种简单且直观的排序算法,它的工作原理是逐步构建有序序列。该算法将待排序的数组分为两部分,一部分是已经排好序的,另一部分是待排序的。而在初始时,第一个数据默认有序(一个数据肯定是有序的),然后逐步将待排序部分的数据插入到已排序部分,直至整个数组有序。
实际中我们玩扑克牌时,就用了插入排序的思想。

具体步骤如下:
- 初始时将待排序的数组分为两部分,第一个元素是有序部分,从第二个元素开始,将其视为当前需要插入的元素,即待排序部分。
- 将该元素与已经排好序的部分从右到左逐个比较,找到合适的位置插入。
- 重复上述过程,直到所有元素都被插入到已排序部分,形成完整的有序序列。

画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

代码如下:
void InsertSort(int* nums, int n)
{
for (int i = 1; i < n ; ++i)
{
int tmp = nums[i];//待插入元素
//开始插入,从待插入区间的最后一个元素开始,从后往前比较
int end = i - 1;
while (end >= 0)
{
if (nums[end] > tmp)
{
nums[end + 1] = nums[end];
--end;
}
else
{
break;
}
}
nums[end + 1] = tmp;
}
}
插入排序是一种稳定的排序算法,它的时间复杂度为O(n^2),其中n是数组的长度。缺点:插入排序在大规模数据上性能相对较差。优点:实现简单且在小规模或部分有序的数据集上表现良好,有时候也可作为其他排序算法的优化步骤。
2. 希尔排序
算法思想:希尔排序是由Donald Shell于1959年提出的一种排序算法,是对插入排序的一种改进,也被称为缩小增量排序。希尔排序解决了插入排序在处理大规模数据时的性能不足的问题。希尔排序的核心思想是通过对原始数组的分组排序,然后对每一组分别进行插入排序,然后逐步减小分组的间隔,直到间隔为1,最终完成整体的排序。
具体步骤如下:
- 选择分组间隔: 选择一个整数gap作为分组间隔,这个整数的选择对算法性能有很大影响。常见的分组间隔有希尔原始提出的gap = n / 2。
- 分组插入排序: 根据选择的分组间隔gap,将数组划分为gap组。对每个分组进行插入排序,即在每个分组内部进行局部排序。
- 逐步缩小分组间隔: 重复上述步骤,逐步缩小分组间隔,直到分组间隔为1。这时,算法转变为普通的插入排序,但由于此时数组已经基本有序,插入排序的工作量相对较小。
画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

代码如下:
void ShellSort(int* nums, int n)
{
int gap = n;
while (gap > 1)
{
gap /= 2;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = nums[end + gap];
while (end >= 0)
{
if (nums[end] > tmp)
{
nums[end + gap] = nums[end];
end -= gap;
}
else
{
break;
}
}
nums[end + gap] = tmp;
}
}
}
希尔排序的性能分析较为复杂,因为它依赖于分组间隔gap选择。在最坏情况下,希尔排序的时间复杂度为O(n^2),但在实际应用中,它的平均时间复杂度约为O(nlogn)。
以下是一些书上对希尔排序时间复杂度的计算:
《数据结构(C语言版)》— 严蔚敏

《数据结构-用面相对象方法与C++描述》— 殷人昆

因为咱们的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时就按照:O(n^1.25)到 O(1.6 * n^1.25)来算。
希尔排序是一种不稳定的排序算法,即相同元素的相对位置在排序前后可能会改变(因为相同元素可能被分在不同的组,从而导致相对位置发生改变)。尽管有一些更高效的排序算法,希尔排序仍然因其相对简单的实现和在某些特定场景下的性能表现而受到一定的关注。
3. 选择排序
算法思想:选择排序是一种简单且直观的排序算法,它的基本思想是在未排序的部分中选择最小(或最大)的元素,然后将其与未排序部分的第一个元素进行交换。这个过程不断重复,直到所有元素都有序。
具体步骤如下:
- 初始状态: 将整个待排序的数组分为两部分,已排序部分和未排序部分。初始时已排序部分为空,未排序部分包含所有元素。
- 选择最小元素: 在未排序部分中选择最小的元素,记录其位置。
- 交换位置: 将选中的最小元素与未排序部分的第一个元素交换位置,将其纳入已排序部分。
- 重复步骤: 重复上述过程,从未排序部分选择最小元素并交换,直到所有元素都有序。

画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

代码如下:
void SelectSort(int* nums, int n)
{
//选n - 1次,同时i位置为未排序部分的第一个元素的下标
for (int i = 0; i < n - 1; ++i)
{
int mini = i;
//从未排序部分找最小值与未排序部分第一个元素交换
for (int j = i + 1; j < n; j++)
{
if (nums[j] < nums[mini])
{
mini = j;
}
}
Swap(&nums[mini], &nums[i]);
}
}
选择排序的特点是每次找到未排序部分的最小元素,并将其放到已排序部分的末尾。它的时间复杂度为O(n^2),其中n是数组的长度。选择排序是一种不稳定的排序算法,因为相同大小的元素在排序后可能会改变相对位置。选择排序相对简单,但由于其时间复杂度较高,不适合对大规模数据进行排序。
4. 堆排序
堆排序是一种基于二叉堆数据结构的排序算法。它利用了堆的性质来实现对元素的高效排序。堆排序分为两个阶段:建堆和排序。之前写的这篇文章,里面详细介绍了堆排序,本文就不做赘述了。链接如下:堆排序讲解
5. 冒泡排序
算法思想:冒泡排序是一种基础的排序算法,也是我们最熟悉(第一个接触)的排序算法。它的工作原理是反复遍历待排序的元素序列,比较相邻的两个元素,如果它们的顺序不符合要求(例如,升序排序时前面的元素大于其相邻后面的元素),则交换它们的位置。通过这样的交换操作,每一轮遍历都能将未排序部分的最大元素冒泡到最后,因此得名冒泡排序。
具体步骤如下:
- 比较相邻元素: 从数组的第一个元素开始,与相邻的元素进行比较。
- 交换位置: 如果顺序不符合要求,交换这两个元素的位置,使得较大(或较小)的元素交换到数组的末尾。
- 遍历未排序部分: 重复上述比较和交换步骤,遍历未排序部分,直到整个数组有序。

画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

代码如下:
void BubbleSort(int* nums, int n)
{
//比较趟数n - 1;
for (int i = 0; i < n - 1; ++i)
{
int flag = 0;
//每趟比较次数 n - 1 - i
for (int j = 0; j < n - 1 - i; ++j)
{
if (nums[j] > nums[j + 1])
{
flag = 1;
Swap(&nums[j], &nums[j + 1]);
}
}
if (0 == flag)
{
break;
}
}
}
冒泡排序的时间复杂度为O(n^2),其中n是数组的长度。它是一种稳定的排序算法,即相同元素的相对位置在排序前后不会改变。尽管冒泡排序的性能相对较差,特别是对于大规模数据集,但由于其实现方式简单易懂,它常被用于教学和理解排序算法的基本原理。
6. 快速排序
6.1 快速排序(递归版本)
算法思想:快速排序是一种基于分治思想的排序算法,由英国计算机科学家Tony Hoare于1960年提出。它的主要思想是选择一个基准元素,将数组分成两个子数组,使得基准元素左边数组的元素都小于基准元素,使得基准元素右边数组的元素都大于基准元素,然后对这两个数组重复上述操作,直到整个数组有序。
具体步骤如下:
- 选择基准:从数组中选择一个元素作为基准元素。选择基准的方式可以有多种,常见的包括取第一个元素、最后一个元素、中间元素或随机选择。
- 划分:将数组中小于基准元素的元素放在基准的左侧,大于基准元素的元素放在基准的右侧。这个过程称为划分(partition)。
- 递归排序:对划分得到的两个子数组递归地应用快速排序算法。
快速排序的关键点在于选择完基准元素以后如何使得基准元素左边数组的元素都小于基准元素,使得基准元素右边数组的元素都大于基准元素,下面给出了三种方法我们来分别介绍一下:
方法一(hoare版本):
具体步骤:
-
选择基准元素:选择数组中的一个元素作为基准(通常选择第一个元素)。
-
初始化指针:初始化两个指针,一个指向数组的开头,另一个指向数组的末尾。
-
交换元素:从两个指针所指位置开始,分别向中间移动,直到找到需要交换的元素对。
具体规则如下:
向左移动右指针,直到找到一个小于基准的元素。
向右移动左指针,直到找到一个大于基准的元素。
如果左指针仍在右指针的左侧,交换这两个元素。
重复步骤3: 继续重复步骤3,直到左指针与右指针相遇。 -
将基准元素放置到正确位置: 当左指针超过右指针时,将基准元素与右指针所指位置的元素进行交换。
-
返回基准位置: 返回左指针的位置作为新的基准位置。

画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

代码如下:
//hore版本
int part1(int* nums, int left, int right)
{
keyi = left;//第一个元素做key
while (left < right)
{
//右边找小
while (left < right && nums[right] >= nums[keyi])
{
--right;
}
//左边找大
while (left < right && nums[left] <= nums[keyi])
{
++left;
}
Swap(&nums[left], &nums[right]);交换left和right位置的元素
}
Swap(&nums[keyi], &nums[left]);
return left;
}
方法二(挖坑法):
具体步骤:
- 选择基准元素:选择数组中的一个元素作为基准(通常选择第一个元素),将基准元素保存起来,初始时,基准元素所在位置为坑位(记为hole),也就是left指向的位置。
- 初始化指针:初始化两个指针,一个指向数组的开头,另一个指向数组的末尾。
- 挖坑操作:
- 从右指针位置开始,找到小于基准的元素,将其填入坑里,此时right指向的位置为新的坑位,更新hole。
如果右指针位置的元素大于或等于基准,右指针左移。
如果右指针位置的元素小于基准,将该元素填入坑里。 - 从左指针位置开始,找到大于基准的元素,将其填入填入坑里,此时left指向的位置为新的坑位,更新hole。
如果左指针位置的元素小于或等于基准,左指针右移。
如果左指针位置的元素大于基准,将该元素填入填入坑里。
重复步骤3和步骤4: 重复上述挖坑操作,直到左指针与右指针相遇。
-
填坑:将基准元素填入最后一个坑的位置。
-
返回基准位置:返回hole的位置作为新的基准位置。

画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

代码如下:
int part2(int* nums, int left, int right)
{
//保存key并记录hole的位置
int key = nums[left];
int hole = left;
while (left < right)
{
//右边找小
while (left < right && nums[right] >= key)
{
--right;
}
nums[hole] = nums[right];
hole = right;
//左边找大
while (left < right && nums[left] <= key)
{
++left;
}
nums[hole] = nums[left];
hole = left;
}
nums[hole] = key;
return hole;
}
方法三(前后指针法):
具体步骤:
- 选择基准元素:选择数组中的一个元素作为基准(通常选择第一个元素)。
- 初始化指针:初始化两个指针,一个指向数组的开头记为prev,另一个指向数组的开头的下一个元素记为cur。
- 前后指针划分:cur开始向右移动,如果cur指向的元素比key小,prev先向右移动一步,然后交换prev位置和cur位置的元素,cur向右移动一步;如果cur指向的元素比key大,cur继续向右移动,直到找到比key小的元素在停下来。重复上面的操作,直到cur走完整个数组,最后将prev位置的元素和key所在的位置的元素交换。
- 返回基准位置: 返回prev的位置作为新的基准位置。

画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

代码如下:
int part3(int* nums, int left, int right)
{
keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (nums[cur] < nums[keyi] && ++prev != cur)
{
Swap(&nums[prev], &nums[cur]);
}
++cur;
}
Swap(&nums[keyi], &nums[prev]);
return prev;
}
通过上面三种方法中的任意一种方法,都能使得选取的基准元素被放置在正确的位置上,并划分出左右两个子区间。然后将划分后的左右子区间分别作为新的待排序数组,对它们进行递归排序。这个过程是快速排序的核心思想,通过不断划分和递归,最终完成整个数组的排序。
画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

快排递归版本完整代码如下:
//hoare版本
int part1(int* nums, int left, int right)
{
keyi = left;
while (left < right)
{
//右边找小
while (left < right && nums[right] >= nums[keyi])
{
--right;
}
//左边找大
while (left < right && nums[left] <= nums[keyi])
{
++left;
}
Swap(&nums[left], &nums[right]);
}
Swap(&nums[keyi], &nums[left]);
return left;
}
//void QuickSort(int* nums, int left, int right)
{
if (left >= right) return;
int keyi = part1(nums, left, right);
QuickSort(nums, left, keyi - 1);
QuickSort(nums, keyi + 1, right);
}
6.2 快速排序(非递归版本之三路划分)
三路划分快速排序是对传统快速排序的一种改进,主要解决了在数组中存在大量重复元素时性能下降的问题。它通过将数组划分为三个部分,分别存放小于、等于和大于基准元素的元素,以减少重复元素的比较和交换。以下是三路划分快速排序的详细介绍:
- 选择基准元素: 选择数组中的一个元素作为基准(通常选择第一个元素)。
- 初始化指针: 初始化三个指针,left, right, cur。
- 三路划分: 遍历数组,将数组划分为三个部分:
小于基准的部分(nums[begin, left-1])
等于基准的部分(nums[left, right])
大于基准的部分(nums[right+1, end]) - 遍历过程: 对于当前元素 nums[cur]:
如果 nums[cur] 小于基准,则将其与 nums[left] 交换,然后递增 left 和 cur。
如果 nums[cur] 等于基准,则递增 cur。
如果 nums[cur] 大于基准,则将其与 nums[right] 交换,然后递减 right。 - 递归排序: 对小于和大于基准的两个部分进行递归排序。
画个图理解一下:
假设待排序数组是:{ 6, 3, 6, 7, 6, 5, 2, 4 }。

代码如下:
void QuickSort(int* nums, int begin, int end)
{
if (begin >= end) return;
int key = nums[begin];
int left = begin, right = end, cur = left + 1;
//三路划分
while (cur <= right)
{
if (nums[cur] < key)
{
Swap(&nums[left++], &nums[cur++]);
}
else if (nums[cur] > key)
{
Swap(&nums[right--], &nums[cur]);
}
else
{
cur++;
}
}
//递归处理大于key和小于key的部分。
QuickSort(nums, begin, left - 1);
QuickSort(nums, right + 1, end);
}
6.3 快速排序(非递归版本C++实现)
快速排序的非递归版本通常使用栈来模拟递归的过程。非递归实现的关键在于手动管理递归调用的栈,并使用迭代来替代递归。由于需要栈的辅助因此,非递归版本使用C++实现。
具体步骤如下:
- 选择基准元素:从待排序数组中选择一个基准元素,通常选择数组的第一个元素。
- 初始化栈:使用一个栈来存储待排序子数组的边界。初始时,将整个数组的边界入栈。
- 迭代处理:迭代地从栈中取出边界,对相应的子数组执行划分操作,将划分后的两个子数组的边界入栈。这个过程一直持续,直到栈为空。
- 划分操作:在每一次迭代中,执行划分操作,将数组划分为两部分,左边部分的元素小于等于基准元素,右边部分的元素大于基准元素,并返回基准元素的最终位置。
- 栈操作:将划分后的子数组的边界入栈,以便后续对它们进行划分。根据问题的规模,选择是先处理左子数组还是右子数组,或者两者顺序都入栈。
- 重复步骤 3-5:重复迭代、划分和栈操作的过程,直到栈为空。
画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

代码如下:
int part1(vector<int>& nums, int left, int right)
{
int keyi = left;
while (left < right)
{
//右边找小
while (left < right && nums[right] >= nums[keyi])
{
--right;
}
//左边找大
while (left < right && nums[left] <= nums[keyi])
{
++left;
}
swap(nums[left], nums[right]);
}
swap(nums[keyi], nums[left]);
return left;
}
vector<int> sortArray(vector<int>& nums)
{
stack<int> st;
//初始时,将整个数组的边界入栈
st.push(0);
st.push(nums.size() - 1);
//迭代地从栈中取出边界,对相应的子数组执行划分操作
while (!st.empty())
{
int right = st.top();
st.pop();
int left = st.top();
st.pop();
int keyi = part1(nums, left, right);
//将划分后的两个子数组的边界入栈
if (keyi + 1 < right)
{
st.push(keyi + 1);
st.push(right);
}
if (keyi - 1 > left)
{
st.push(left);
st.push(keyi - 1);
}
}
return nums;
}
};
6.3 快速排序优化
6.3.1 三数取中法选key。
采用三数取中法选择中间值作为 key 是为了避免在已经有序的情况下发生最坏情况。
在快速排序中,选择合适的key是影响算法性能的关键之一。当选择待排序区间的最左侧元素作为key时,在数组已经有序或者近乎有序的情况下,可能导致快速排序的性能下降。这是因为在这种情况下,每次划分都可能得到一个极端不平衡的划分,使得一个子数组的大小为0,而另一个子数组的大小为原来的规模减1。
通过使用三数取中法,选择待排序区间的左端、右端和中间的三个元素中的中值作为key,可以有效地减少出现最坏情况的概率。这是因为无论数组的有序性如何,取三个元素的中值可以保证key相对于整个数组是比较中间的位置,从而减小了出现不平衡划分的可能性。
三数取中法的具体步骤如下:
- 选择待排序区间的左端、右端和中间的三个元素。2.
- 比较这三个元素,找到其中值最中间的元素。
- 将三者的中间值作为key。
这样,采用三数取中法可以在一定程度上提高快速排序在各种情况下的性能表现。
三数取中代码如下:
//快排优化 三数取中
int GetMidIndex(int* nums, int left, int right)
{
int mid = left + (right - left) / 2;
if (nums[left] < nums[mid])
{
if (nums[mid] < nums[right])
{
return mid;
}
else if (nums[left] < nums[right])
{
return right;
}
else
{
return left;
}
}
else//nums[left] > nums[mid]
{
if (nums[mid] > nums[right])
{
return mid;
}
else if (nums[left] > nums[right])
{
return right;
}
else
{
return left;
}
}
}
6.3.2 递归到小的子区间时,可以考虑使用插入排序。
优化快速排序的另一种常见策略就是在递归到小的子区间时切换到插入排序。这是因为插入排序在小规模数据上的表现通常比快速排序更好,因为它的常数因子较小。
快速排序的基本思想是对大规模数据进行分治,但在递归到一定程度时,如果子数组足够小,快速排序的递归开销可能会超过插入排序的实际排序时间。因此,切换到插入排序可以在小规模数据上提高性能。
以下是一种在实际实现中可以考虑的快速排序和插入排序结合的策略:
-
判断递归停止条件:在每次递归之前,先判断子数组的大小是否小于某个阈值(通常是5到20之间)。如果小于阈值,则停止递归。
-
插入排序:当子数组的大小小于阈值时,切换到插入排序。插入排序对于小规模数组的性能通常较好,因为它的常数因子小且不涉及递归。
-
继续递归:如果子数组的大小超过阈值,继续进行快速排序的递归步骤。
这种策略被称为“递归深度限制”或“混合排序”策略。通过这种方式,可以在保持快速排序的优越性能的同时,避免了在小规模数据上的不必要的递归开销。这个阈值的选择可以根据具体问题和性能需求进行调整。
6.3.3 优化后的快速排序完整代码
void Swap(int* e1, int* e2)
{
int tmp = *e1;
*e1 = *e2;
*e2 = tmp;
}
void InsertSort(int* nums, int n)
{
for (int i = 1; i < n ; ++i)
{
int tmp = nums[i];//待插入元素
//开始插入,从待插入区间的最后一个元素开始,从后往前比较
int end = i - 1;
while (end >= 0)
{
if (nums[end] > tmp)
{
nums[end + 1] = nums[end];
--end;
}
else
{
break;
}
}
nums[end + 1] = tmp;
}
}
//快排优化 三数取中
int GetMidIndex(int* nums, int left, int right)
{
int mid = left + (right - left) / 2;
if (nums[left] < nums[mid])
{
if (nums[mid] < nums[right])
{
return mid;
}
else if (nums[left] < nums[right])
{
return right;
}
else
{
return left;
}
}
else//nums[left] > nums[mid]
{
if (nums[mid] > nums[right])
{
return mid;
}
else if (nums[left] > nums[right])
{
return right;
}
else
{
return left;
}
}
}
//hoare版本
int part1(int* nums, int left, int right)
{
int keyi = GetMidIndex(nums, left, right);
Swap(&nums[left], &nums[keyi]);
keyi = left;
while (left < right)
{
//右边找小
while (left < right && nums[right] >= nums[keyi])
{
--right;
}
//左边找大
while (left < right && nums[left] <= nums[keyi])
{
++left;
}
Swap(&nums[left], &nums[right]);
}
Swap(&nums[keyi], &nums[left]);
return left;
}
void QuickSort(int* nums, int left, int right)
{
if (left >= right) return;
//当子数组的大小小于阈值时,切换到插入排序。
if (right - left < 10)
{
InsertSort(nums, right - left + 1);
}
int keyi = part1(nums, left, right);
QuickSort(nums, left, keyi - 1);
QuickSort(nums, keyi + 1, right);
}
7. 归并排序
7.1 归并排序(递归版本)
算法思想:归并排序是一种基于分治思想的经典排序算法。它将一个未排序的数组分割成两个子数组,分别对这两个子数组进行排序,然后将排序后的子数组合并为一个有序数组。这个过程递归进行,直到整个数组有序。时间复杂度O(n*longn),空间复杂度O(n)。
具体详细步骤如下:
- 分割:将未排序的数组分割成两个子数组,计算中间位置(mid)。如果数组大小为0或1,则认为已经有序。否则,递归地对左半部分和右半部分进行分割。
- 合并:合并两个有序的子数组,创建一个临时数组来存储合并结果。初始化三个指针,分别指向左子数组的起始位置、右子数组的起始位置以及合并数组的起始位置。比较左右子数组的元素,将较小的元素放入合并数组,并移动相应的指针。当一个子数组的元素全部合并完毕后,将另一个子数组的剩余部分直接复制到合并数组。
- 递归: 递归地对左右子数组执行分割和合并操作,直到每个子数组的大小为1。

画个图理解一下:
假设待排序数组是:{ 6, 3, 8, 7, 1, 5, 2, 4 }。

代码如下:
void _MergeSort(int* nums, int* tmp, int left, int right)
{
//递归出口,数组大小为0或1,则认为已经有序,直接return
if (left >= right) return;
//计算中间位置(mid)
int mid = left + (right - left) / 2;
//递归使左右区间有序
_MergeSort(nums, tmp, left, mid);
_MergeSort(nums, tmp, mid + 1, right);
//归并
int begin1 = left, begin2 = mid + 1, begin3 = left;
while (begin1 <= mid && begin2 <= right)
{
if (nums[begin1] < nums[begin2])
{
tmp[begin3++] = nums[begin1++];
}
else
{
tmp[begin3++] = nums[begin2++];
}
}
while (begin1 <= mid)
{
tmp[begin3++] = nums[begin1++];
}
while (begin2 <= right)
{
tmp[begin3++] = nums[begin2++];
}
//拷贝会原数组
memcpy(nums + left, tmp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* nums, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(nums, tmp, 0, n - 1);
free(tmp);
}
7.2 归并排序(非递归版本)
归并排序的非递归版本通常采用迭代而非递归调用栈的方式。该实现方式使用循环进行数组的划分和合并操作。
具体详细步骤如下:
- 初始化:从小到大合并,首先将待排序数组划分为若干个大小为1的子数组,即每个元素作为一个初始的子数组。
- 迭代合并:通过迭代,不断地将相邻的子数组合并,每次合并后的子数组大小翻倍,直到整个数组有序为止。
- 合并操作:对于每一次合并操作,需要合并两个相邻的子数组。合并过程中,使用额外的空间(通常是临时数组)来存储合并后的结果。
- 循环执行:重复执行迭代和合并的过程,直到整个数组有序。在每一次循环中,对当前子数组进行划分和合并操作。
画个图理解一下:
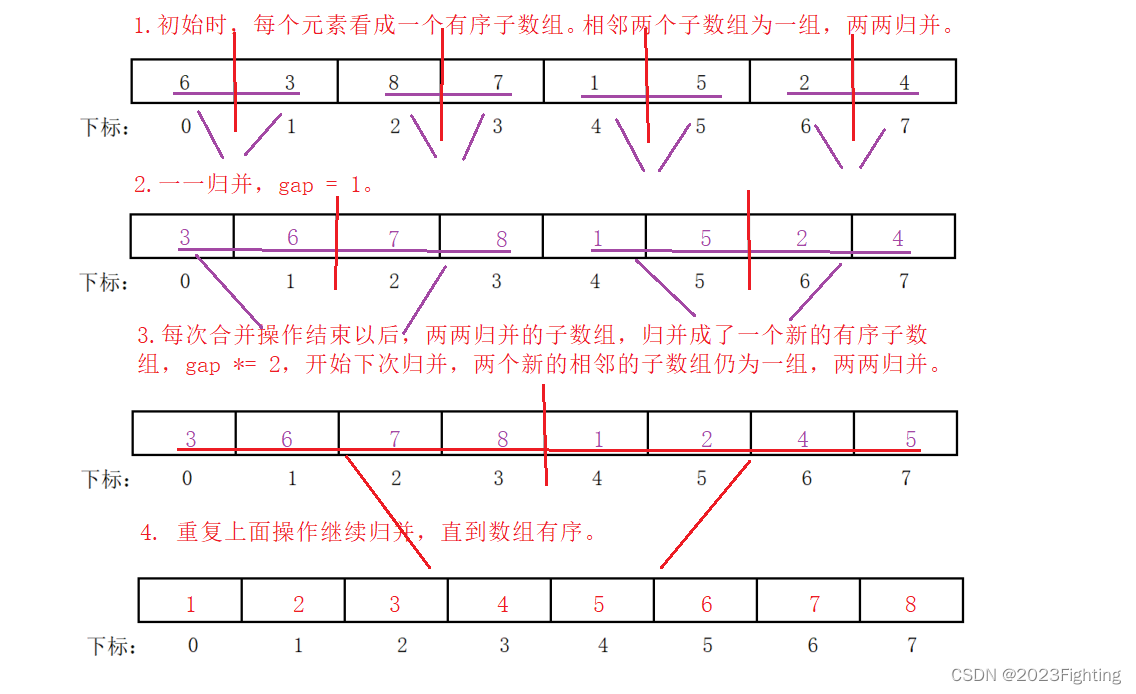
代码如下:
void MergeSortNoR(int* nums, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("MergeSortNoR->malloc fail");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += gap * 2)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + gap * 2 - 1;
int begin3 = i;
//越界修正
if (end1 >= n)
{
end1 = n - 1;
begin2 = n + 1;
end2 = n;
}
else if (begin2 >= n)
{
begin2 = n + 1;
end2 = n;
}
else if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (nums[begin1] < nums[begin2])
{
tmp[begin3++] = nums[begin1++];
}
else
{
tmp[begin3++] = nums[begin2++];
}
}
while (begin1 <= end1)
{
tmp[begin3++] = nums[begin1++];
}
while (begin2 <= end2)
{
tmp[begin3++] = nums[begin2++];
}
//memcpy(nums, tmp, sizeof(int) * (end2 - i + 1));
}
memcpy(nums, tmp, sizeof(int) * n);
gap *= 2;
}
free(tmp);
}
8. 计数排序
算法思想:计数排序是一种非比较性的排序算法,适用于一定范围内的整数排序。它通过统计每个元素的出现次数,然后根据统计信息重写原数组,从而达到排序的目的。计数排序的核心思想是将待排序数据的值映射为额外数组的下标,然后根据其作为下表位置的计数信息,重新构造有序序列。
具体步骤如下:
- 初始化统计数组:创建一个大小为 range + 1 的统计数组,其中 range 表示输入数组中元素的取值范围。
- 统计每个元素的出现次数:遍历输入数组,对每个元素进行计数,并将计数值存储在统计数组的相应位置。
- 累加计数:遍历统计数组,将每个元素的计数值累加上它前面所有元素的计数值,得到每个元素在排序后数组中的位置。
- 构造有序数组:遍历输入数组,根据统计数组中的信息,将每个元素放置到有序数组的正确位置,并将其计数值减一。
画个图理解一下:
假设待排序数组是:{ 6, 3, 5, 2, 6, 5, 2, 4 }。
在统计数组中每个元素出现次数出现,要先遍历数组,找到数组中元素的最大值和最小值,计算出数组的范围。这是因为使用绝对映射(用数组元素的值直接当作下标),可能会造成空间的浪费。比如这组数据{ 1006, 1003, 1005, 1002, 1006, 1005, 1002,10004},让10000当作下标的,我们需要开辟1006个整型大小的空间,然而0-10001这么多个位置都是浪费的,因此这里使用相对映射,数组每个元素减去数组元素中的最小值作为映射的下标。上面例子使用相对映射,只需要开辟5个空间即可,在很大程度上节省了空间。

代码如下:
void CountSort(int* nums, int n)
{
int min = nums[0], max = nums[0];
//找最大 和 最下的元素
for (int i = 1; i < n; ++i)
{
if (nums[i] < min)
{
min = nums[i];
}
if (nums[i] > max)
{
max = nums[i];
}
}
int range = max - min + 1;
int* tmp = (int*)calloc(range, sizeof(int));
if (tmp == NULL)
{
perror("CountSort->malloc");
exit(-1);
}
//统计每个元素出现的次数
for (int i = 0; i < n; ++i)
{
tmp[nums[i] - min]++;
}
int index = 0;
//写回原数组
for (int i = 0; i < range; i++)
{
while (tmp[i]--)
{
nums[index++] = i + min;
}
}
free(tmp);
}
计数排序的特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
- 稳定性:稳定
至此,本片文章就结束了,若本篇内容对您有所帮助,请三连点赞,关注,收藏支持下。
创作不易,白嫖不好,各位的支持和认可,就是我创作的最大动力,我们下篇文章见!
如果本篇博客有任何错误,请批评指教,不胜感激 !!!

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 14-高并发-异步并发
- 动态内存管理——常见错误
- 详解Vue3中的常见的监听事件submit、mouseenter和mouseleave
- allegro画PCB如何设置原点
- 【AI数学】NeRF中的球面谐波函数(Spherical Harmonics)
- 3个加密和保护U盘数据的工具,保障你的数据安全
- QQ失效文件怎么恢复?学会这些方法轻松解决!
- Messari 2023 DePIN 报告解读:AI 融合新方向,亚洲项目将加速涌现
- 密码输入时的隐藏显示和显示
- 零基础学Python(1)— 一文带你了解什么是Python(包括Python解释器安装步骤等)