数据结构和算法-交换排序中的快速排序（演示过程 算法实现 算法效率 稳定性）

发布时间：2024年01月06日

文章目录

总览

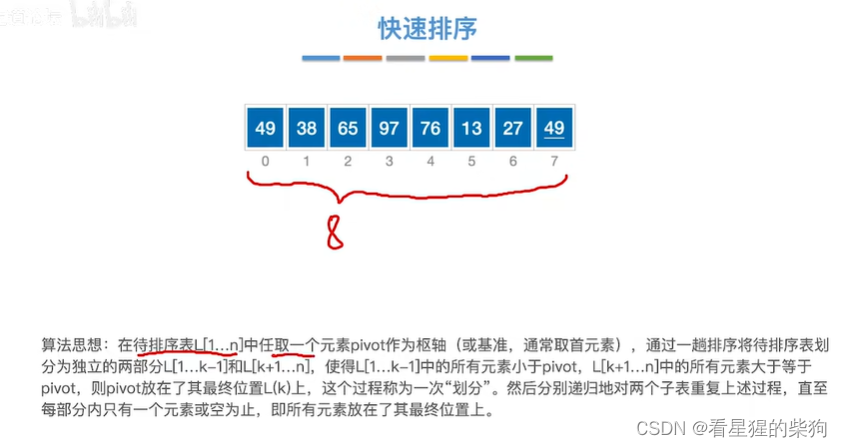
在这里插入图片描述

快速排序（超级重要）

啥是快速排序

在这里插入图片描述

演示过程

此时选49为枢轴元素，接着low和high往中间移动，并且保证，low左边都是小于枢轴元素，high元素右边都是大于枢轴元素
此时high位置的49大于等于49，high左移
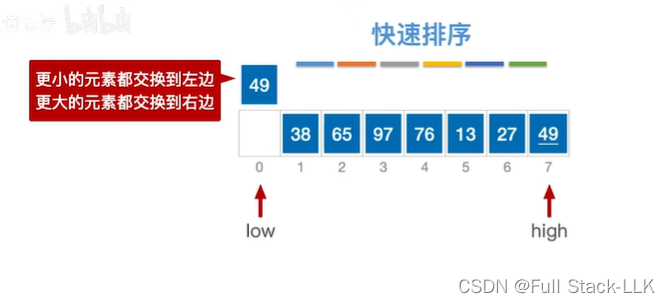
在这里插入图片描述
此时high所指的元素为27小于49，所以将high位置的元素移动到low位置
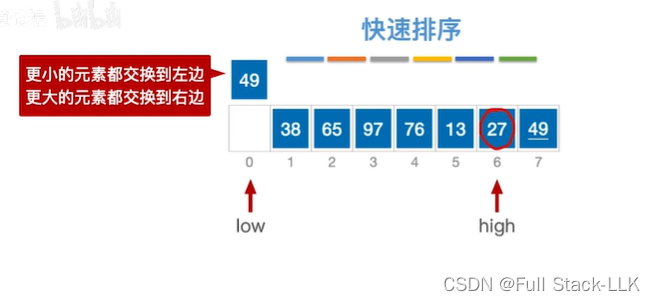
在这里插入图片描述
移动后，high的位置空出来，此时移动low位置，此时low的位置的元素为27，小于49，low移动在这里插入图片描述
此时low位置的元素依然小于49，low移动
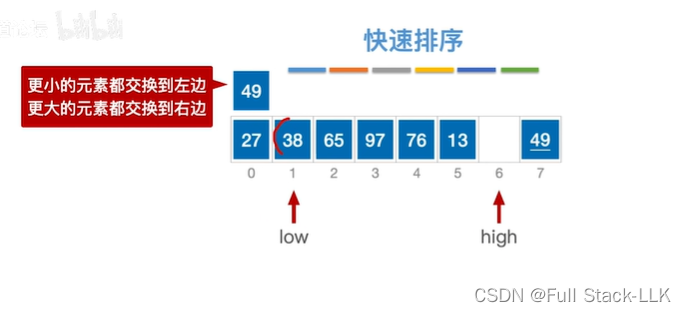
在这里插入图片描述
此时low指向的元素65大于49，移动到high位置
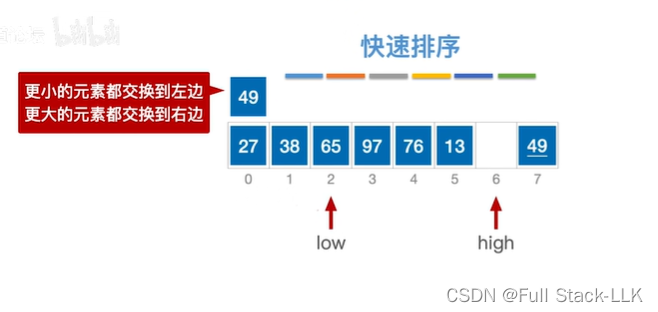
在这里插入图片描述
此时low位置空了，移动high位置，此时high位置的元素大于49，high左移
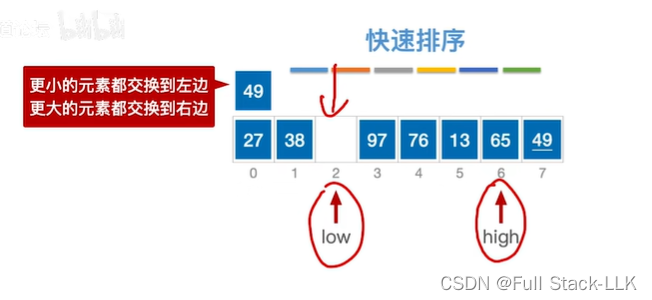
在这里插入图片描述
此时high位置元素13小于49，13移动到low位置，
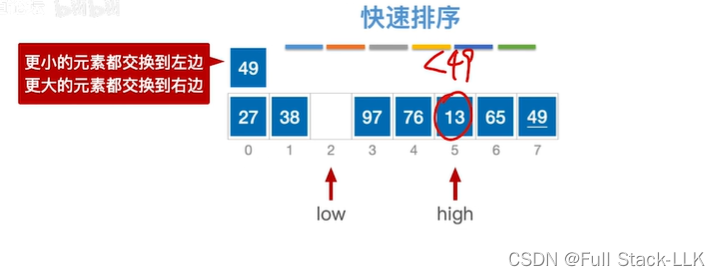
在这里插入图片描述
此时high空，移动low，此时13小于49，low右移
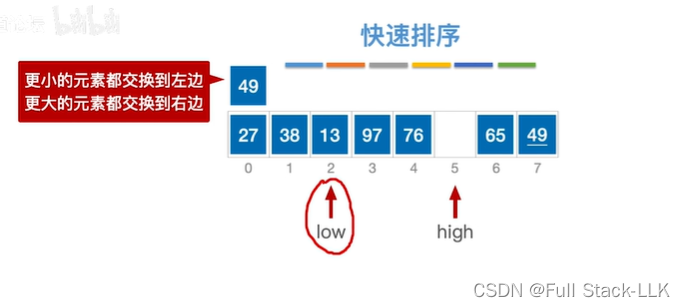
在这里插入图片描述
此时97大于49，将97移动到high

在这里插入图片描述
此时移动high，97大于49，high左移
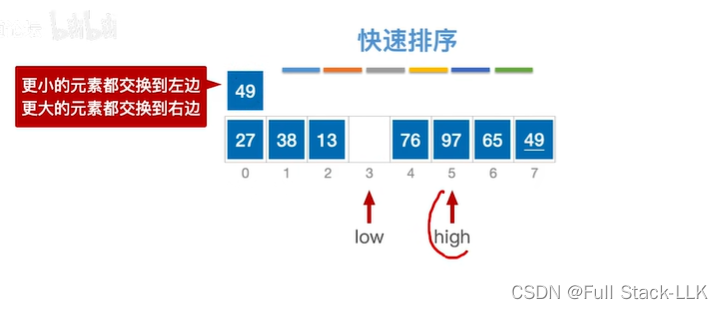
在这里插入图片描述
此时76大于49，high左移
在这里插入图片描述
low和high碰到一起，此时左右元素都扫了一遍了，比49都小的元素都放到low的左边了，比49大的元素都放high的右边，
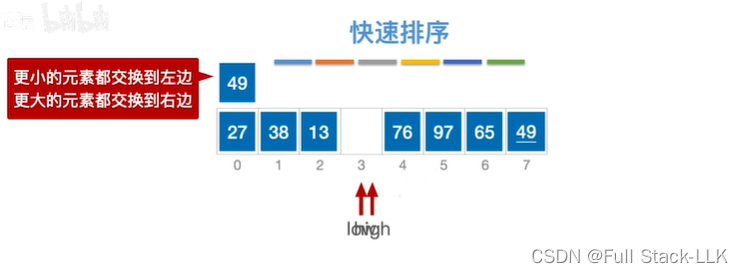
在这里插入图片描述
然后把枢轴元素放到low和high重合的位置
在这里插入图片描述

接下来对分别对左右两个子表进行刚刚的过程
此时是左子表，high位置元素13小于27，移动到low
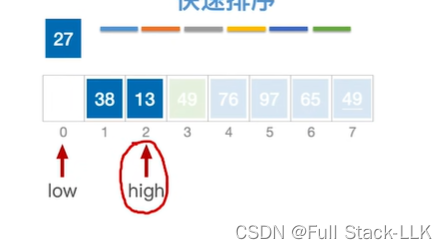
在这里插入图片描述
此时移动low，13小于27，low右移，
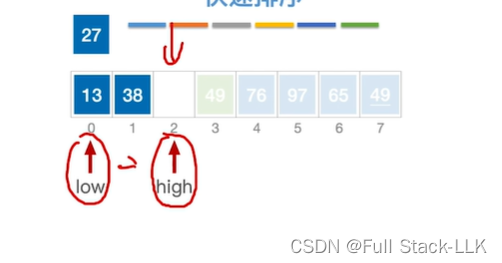
在这里插入图片描述
此时38大于27，38移到high
在这里插入图片描述
此时移动high，38大于27，high左移
在这里插入图片描述
此时high和low重合，27放入该位置
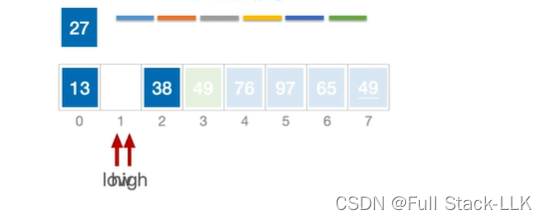
在这里插入图片描述
此时该子表又划分两个子表，此时两个子表都只有一个元素，此时不需要处理，因为此时low左边元素小于枢轴，high右边元素大于枢轴，又因为此时左右都只有一个元素，所以已经有序
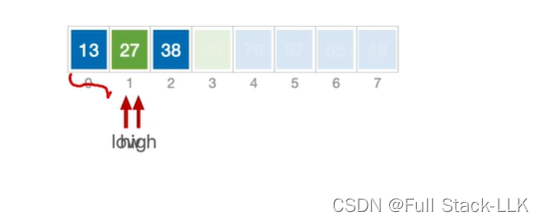
在这里插入图片描述
此时要处理右子表，high所指元素49小于76，49移动到low，
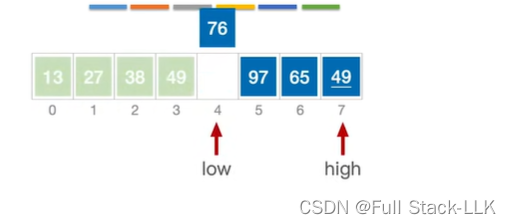
在这里插入图片描述
此时49小于76,low右移动
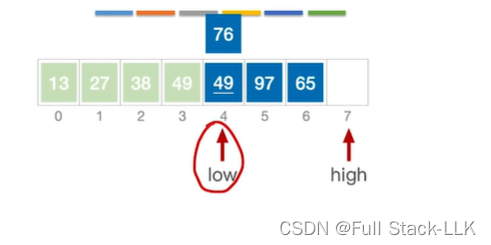
在这里插入图片描述
此时97大于76，97移动到high
在这里插入图片描述
此时high移动，97大于76，high左移
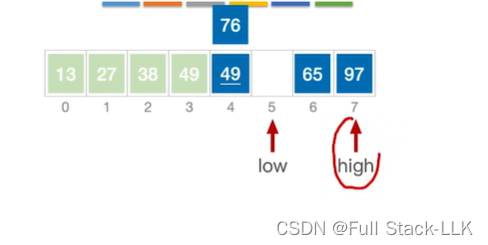
在这里插入图片描述
65小于76，65移动到low
在这里插入图片描述
low移动，65小于76，low右移，
在这里插入图片描述
low和high碰头，76放入该位置
在这里插入图片描述
此时再次划分为两个子表，对左子表处理
此时65大于49，high左移

在这里插入图片描述
low和high碰头，49放该位置

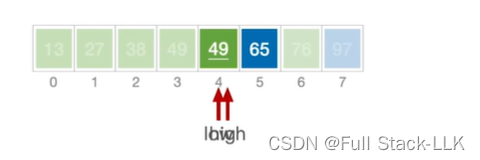
在这里插入图片描述
此时由于65和97都只有一个元素，所以直接确定位置
最后排序结果
在这里插入图片描述

算法实现

在这里插入图片描述

首先调用QuickSor函数，开始对整个表划分，并调用partition函数，此时划分整个表

第一次quicksort函数

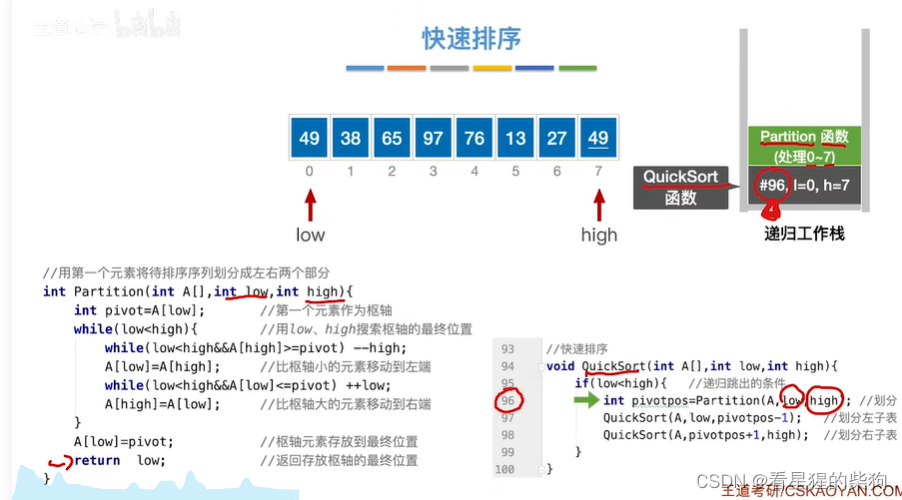
在这里插入图片描述

第一次partion函数

pivot就是枢轴的意思
此时partion函数大循环的条件是low<high，当low=high时将停止循环
此时大循环中还有两个循环，先是high位置开始的循环，然后是low开始的循环
发现49大于要枢轴值
high左移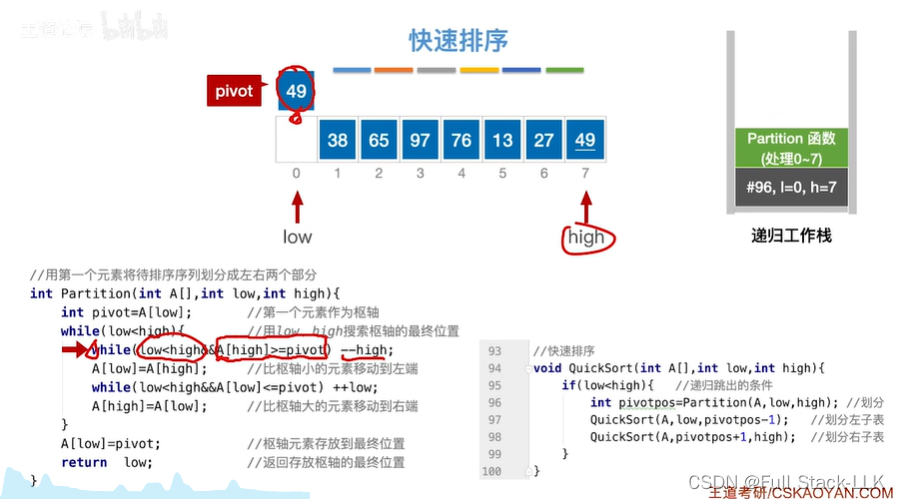在这里插入图片描述
此时27小于枢轴值
跳出while循环，并将此时的high的值赋值给low位置
在这里插入图片描述
此时跳到下一个while循环，比较low位置的值和枢轴的值，如果low的值小于枢轴的值，此时low往后移动
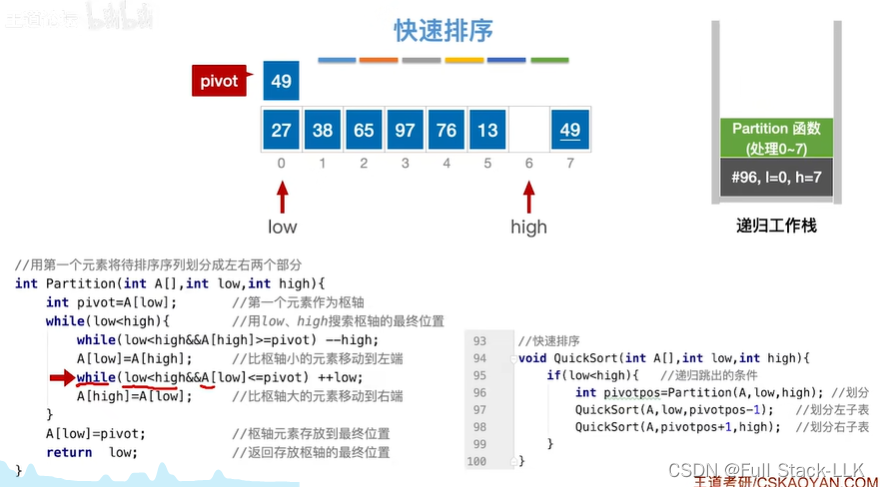
在这里插入图片描述
此时直到65发现low的值大于枢轴的值，跳出循环
此时移动low位置的值到high位置上去，此时回到大循环，发现low<high，继续下一次大循环，但大循环仍然是在溢依次分表之中
在这里插入图片描述
此时继续开始第一次小循环，到13跳出第一次小循环，并将high位置的值给low位置的值

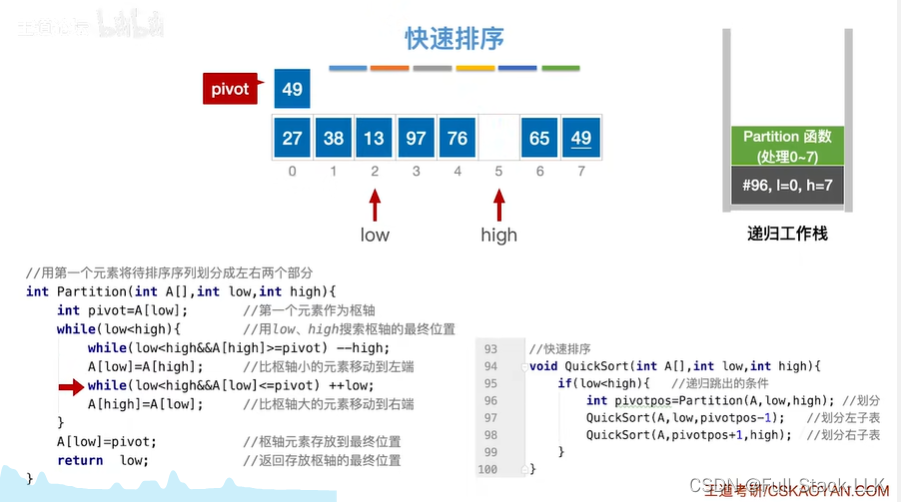
在这里插入图片描述
此时开始第二次小循环，到97跳出第二次小循环，并将low值给high位置的值，然后进入下次大循环
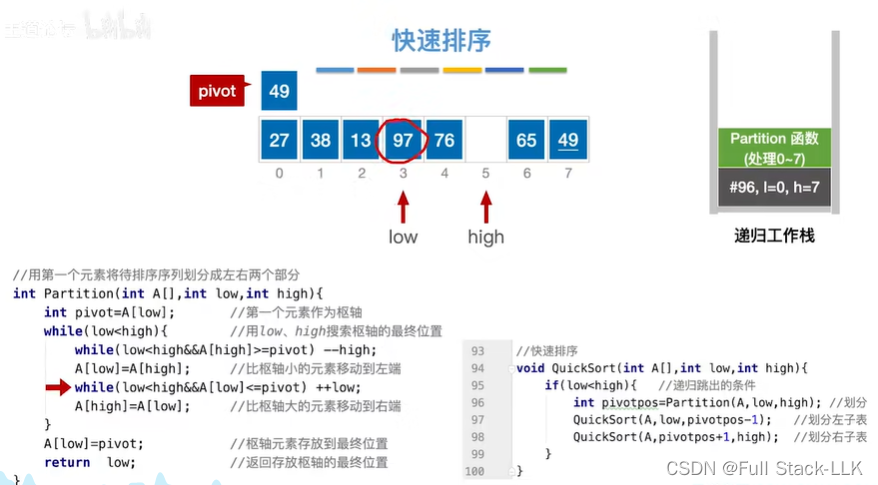
在这里插入图片描述
此时进入第一次小循环，此时当high移动到与low相同才跳出第一次小循环，此时由于low=high，第二次小循环也会跳出，随后大循环条件不满足了，跳出大循环
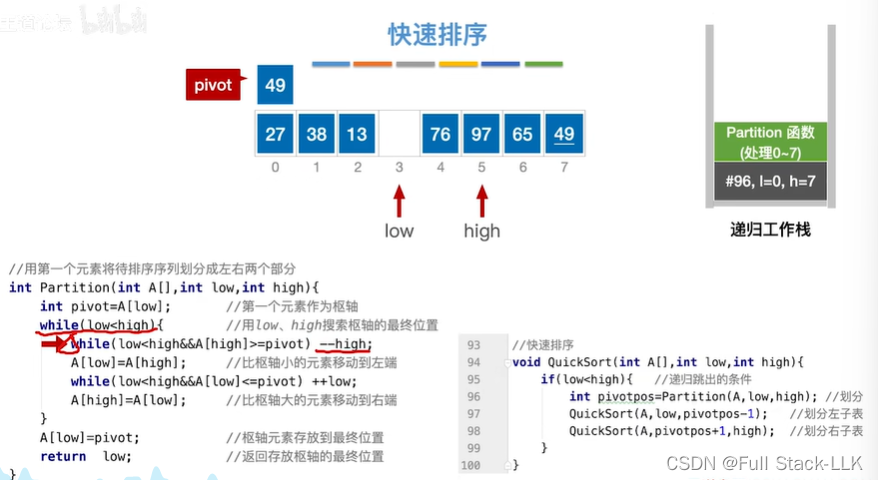
在这里插入图片描述
然后将枢轴元素放到low的位置，并return low的值那么就完成了一次划分的工作
此时quicksort函数中pivotpos的值为该次划分的枢轴的位置
在这里插入图片描述

到第一次quicksort的第一个quicksort

此时处理之前划分的左子表，从low到之前返回得到的枢轴的位置
在这里插入图片描述
此时函数执行过程与之前类似，此时partition函数返回27，返回到第二次quicksort函数中
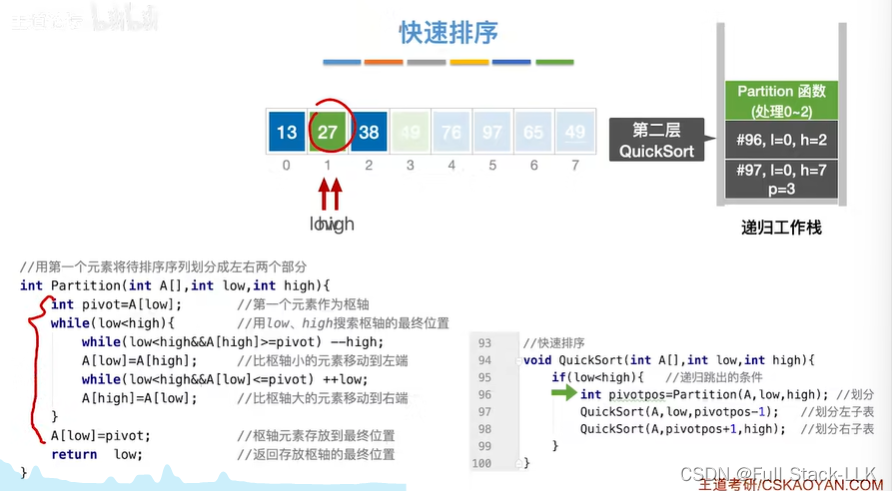
在这里插入图片描述

到第二次quicksort的第一个quicksort

此时的low和high相等，直接跳出if语句
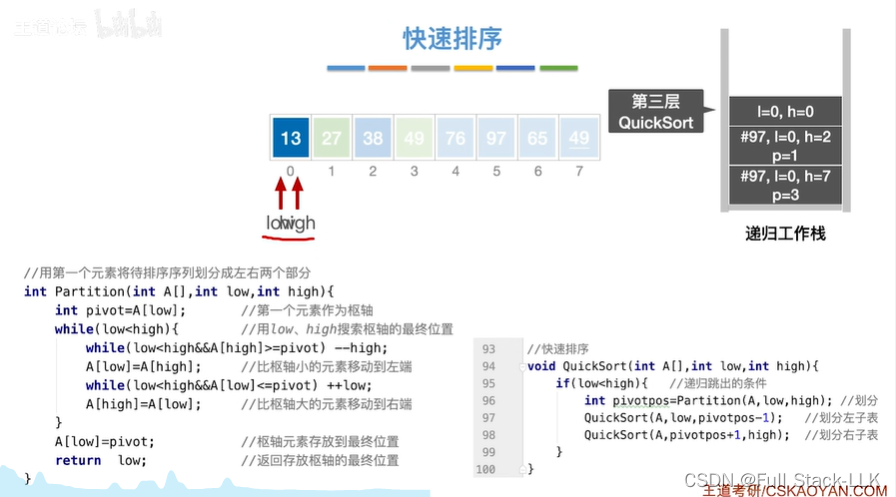
在这里插入图片描述

到第二次quicksort的第二个quicksort

此时low依然等于high，直接跳出if

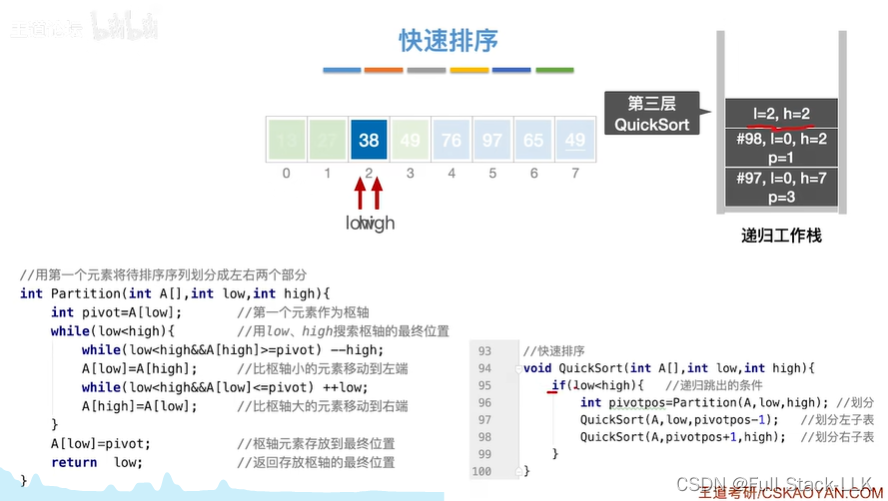
在这里插入图片描述

到第一次quicksort的第二个quicksort

此时low=3+1=4，high=7
在这里插入图片描述

到第一次quicksort的第二个quicksort的partition

执行过程于之前相同
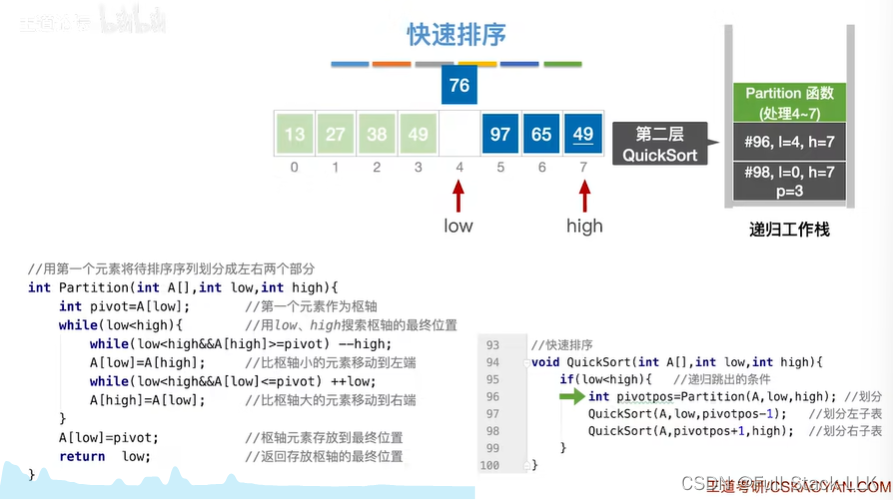
在这里插入图片描述
结果
在这里插入图片描述

到第一次quicksort的第二个quicksort的第一个quicksort

此时之前的partition返回到pivotpos为6
此时的quicksort处理的low为4，high为6-1=5
在这里插入图片描述

到第一次quicksort的第二个quicksort的第一个quicksort的partition函数

此时结果
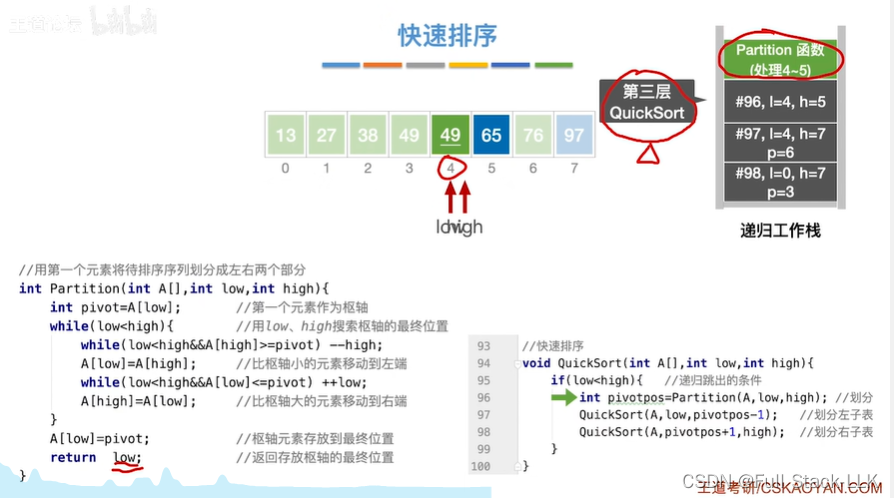
在这里插入图片描述

到第一次quicksort的第二个quicksort的第一个quicksort的第一个quicksort函数

此时之前的partition返回的pivotpos为4
则第一个quicksort对呀的low和4，high为4-1=3
此时不满足low<high，跳出if语句
在这里插入图片描述

到第一次quicksort的第二个quicksort的第一个quicksort的第二个quicksort函数

此时low=4+1=5，high=5，不满足low<high，跳出if语句
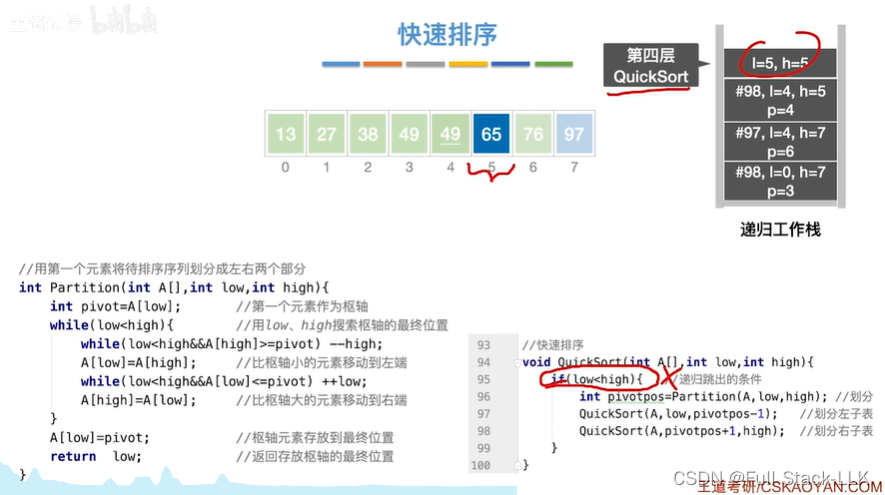
在这里插入图片描述

到第一次quicksort的第二个quicksort的第二个quicksort

此时low=6+1=7，high=7，同样不满足low<high,会跳出if
在这里插入图片描述

第一次quicksort的第二个quicksort执行完

在这里插入图片描述

第一个quicksort执行完

排序完成
在这里插入图片描述

算法效率分析

函数每次先得到该范围的枢轴的位置，然后再以该枢轴为中级元素分开两个范围，对各个范围进行函数

partion函数需要通过low和high将该范围的数据都遍历一遍，因为终止条件是low=high
在这里插入图片描述
此时空间复杂度为调用过程中调用函数栈最多的时候
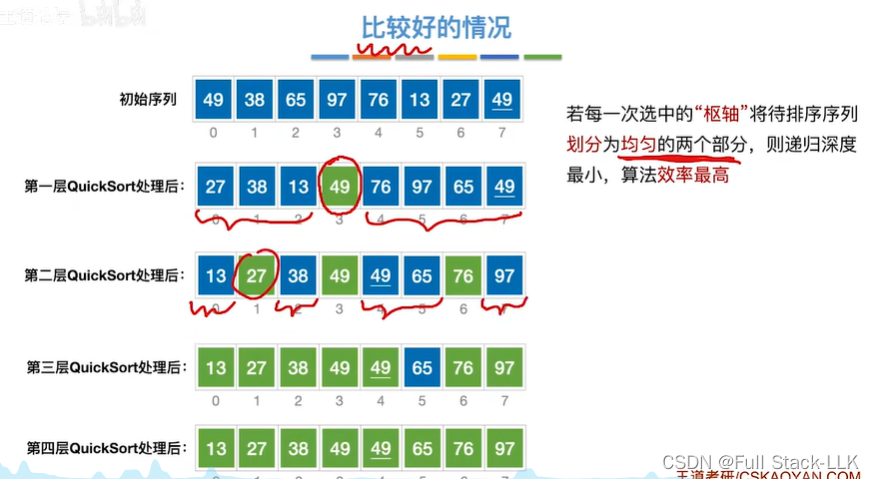
在这里插入图片描述
每层quicksort都是上一层quicksort分成的子表处理，每层处理都分成两个子表在这里插入图片描述
递归层数就是二叉树的层数
在这里插入图片描述

最好的情况

在这里插入图片描述

最坏的情况

在这里插入图片描述
此时high需要左移low才行，第一层quicksort处理后，第二层只需对右边部分处理
在这里插入图片描述
此时依然high需要移到low
在这里插入图片描述
第二层处理后，第三层只需对右边部分处理
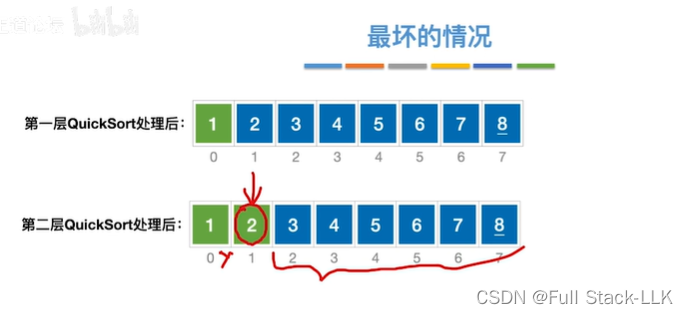
在这里插入图片描述
按照这样，需要8层quicksort调用
如果是逆序，第一层quicksort后，ow移动到最右边的位置即high位置，第二层都只需要处理左边部分，，之后的处理类似
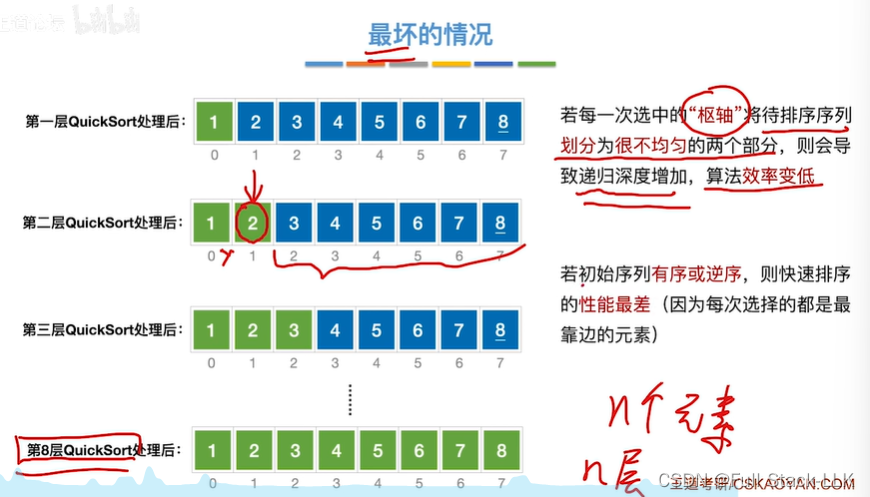
在这里插入图片描述

优化

即让枢轴的值极可能不要是最大值或最小值
在这里插入图片描述

算法效率小结

实际情况实际复杂度都接近于最好时间复杂度
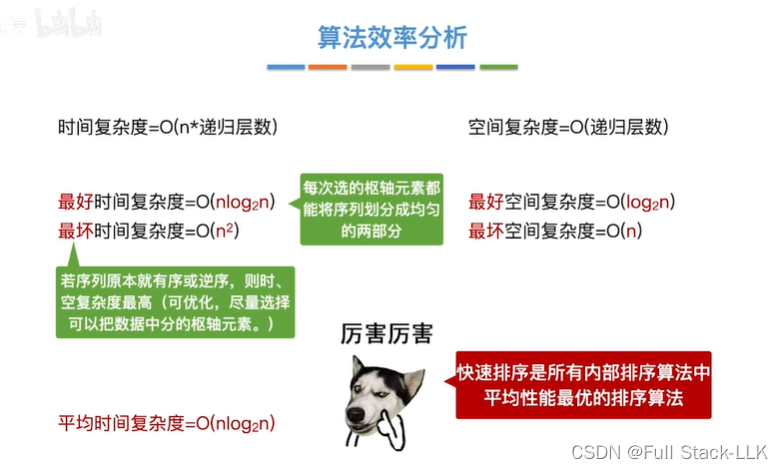
在这里插入图片描述

稳定性

看这个例子
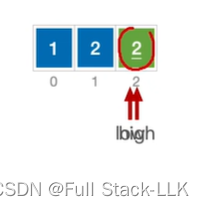
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
是不稳定的
在这里插入图片描述

小结

下图时间复杂度最好和最坏写反了
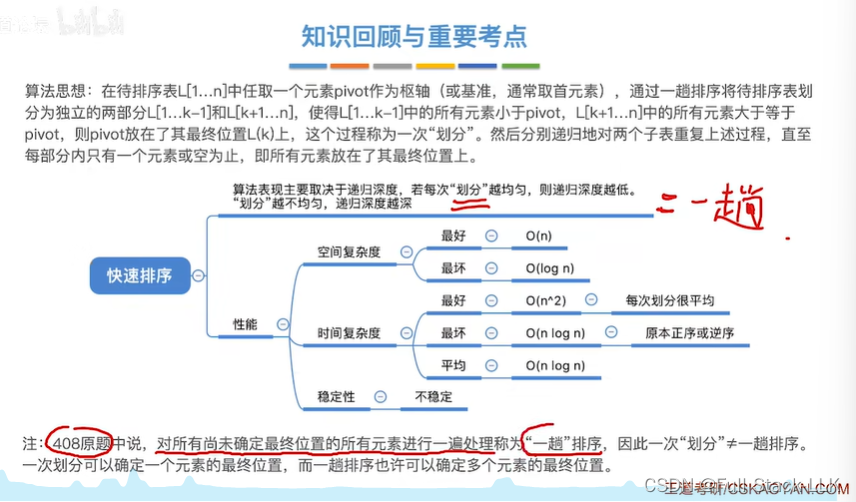
在这里插入图片描述

文章来源:https://blog.csdn.net/llovewuzhengzi/article/details/135427667
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章