【MATLAB随笔】遗传算法优化的BP神经网络(随笔,不是很详细)
一、算法思想
1.1 BP神经网络
BP神经网络(Backpropagation Neural Network,反向传播神经网络)是一种监督学习的人工神经网络,用于模式识别、分类和回归问题。它是一种前馈神经网络,具有至少三层神经元:输入层、隐层(也可以有多个隐层)、输出层。BP神经网络通过训练来调整权值,以最小化预测输出与实际输出之间的误差。
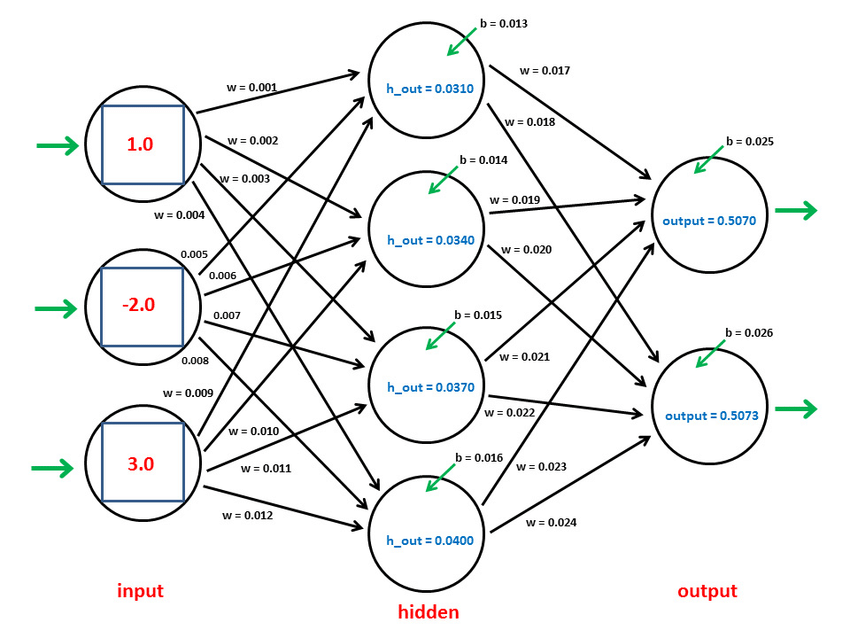
以下是BP神经网络的主要特点和工作原理:
- 前馈结构: BP神经网络是一种前馈结构,信息从输入层经过隐层传递到输出层,没有反馈循环。这意味着信号只沿一个方向传播,从输入到输出。
- 权值调整: BP网络通过使用反向传播算法进行训练,该算法基于梯度下降。在训练过程中,网络通过比较实际输出和期望输出之间的误差,然后将误差通过网络反向传播,调整连接权重以减小误差。
- 激活函数: 在隐层和输出层的神经元上使用激活函数,通常是S型函数(sigmoid)或双曲正切函数(tanh)。这些函数引入非线性性,使得神经网络能够学习非线性关系。
- 误差反向传播: 训练过程中的核心是误差反向传播。它包括前向传播计算输出,计算误差,然后反向传播误差,更新权值。这个过程通过使用梯度下降法来最小化误差。
- 目标函数: 在训练中,BP网络的目标是最小化损失函数,该函数通常是实际输出与期望输出之间差的平方和。
- 局部最小值: BP网络存在陷入局部最小值的风险。为了减轻这个问题,通常采用一些启发式方法或训练多个网络的方法。
它的性能高度依赖于网络结构的选择、学习率的设置以及数据的质量。
传递函数:
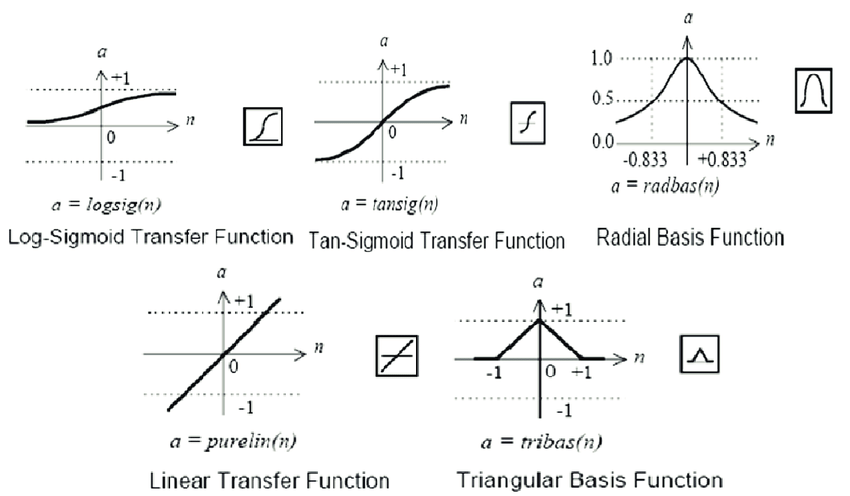
训练函数:
| 训练函数 | 算法 |
|---|---|
'trainlm' | Levenberg-Marquardt |
'trainbr' | 贝叶斯正则化 |
'trainbfg' | BFGS 拟牛顿 |
'trainrp' | 弹性反向传播 |
'trainscg' | 量化共轭梯度 |
'traincgb' | 带 Powell/Beale 重启的共轭梯度 |
'traincgf' | Fletcher-Powell 共轭梯度 |
'traincgp' | Polak-Ribiére 共轭梯度 |
'trainoss' | 单步正割 |
'traingdx' | 可变学习率梯度下降 |
'traingdm' | 带动量的梯度下降 |
'traingd' | 梯度下降 |
1.2 遗传算法
遗传算法(Genetic Algorithm,简称GA)是一种受到生物进化理论启发的优化算法,用于寻找复杂问题的最优解或近似最优解。遗传算法模拟了生物进化过程中的自然选择和遗传机制,通过群体中个体之间的遗传操作来搜索解空间。
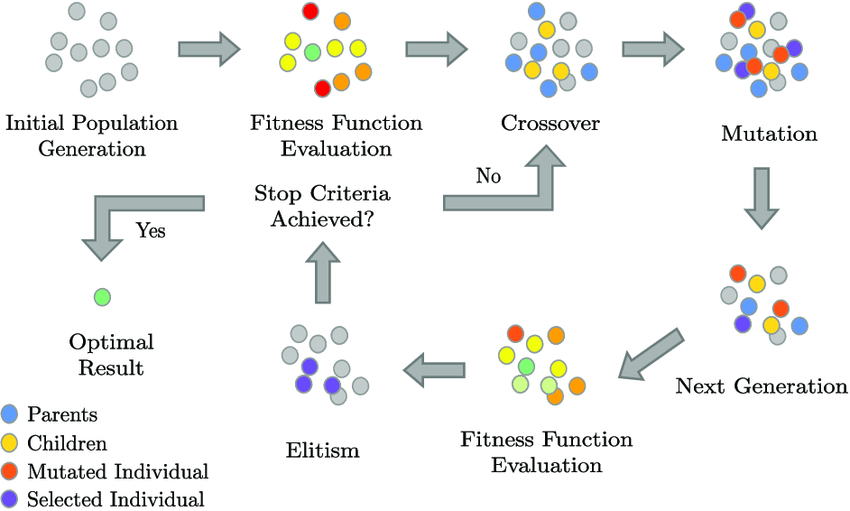
以下是遗传算法的基本步骤和概念:
- 初始化种群: 随机生成初始群体,每个个体都表示问题的一个潜在解。这些个体形成了种群。
- 适应度评估: 对每个个体计算适应度,该适应度指标通常是问题特定的目标函数。适应度表示个体的优劣程度。
- 选择: 根据适应度值进行选择,优秀的个体有更大的概率被选择用于交叉和变异。常用的选择方法包括轮盘赌选择、锦标赛选择等。
- 交叉(交叉操作): 从已选择的个体中选择一对或多对进行交叉,产生新的个体。交叉操作模拟了生物的基因重组过程。
- 变异: 对一些个体进行变异操作,通过微小的改变来引入新的基因。变异操作增加了种群的多样性。
- 新种群形成: 将经过选择、交叉和变异的个体形成新的种群。
- 收敛检查: 检查是否满足停止条件,例如达到最大迭代次数或找到满足要求的解。
- 重复: 如果停止条件未满足,重复从第2步到第7步,直到满足停止条件。
遗传算法的优点包括对复杂搜索空间的全局搜索能力、并行性和对非线性、非凸问题的适应性。然而,它们的性能高度依赖于参数的选择、问题的特性以及适应度函数的设计。
选择遗传算法的参数选择:
- Generations(迭代次数): 较大的迭代次数有助于算法更全面地搜索解空间,但也会增加计算成本。开始时,可以尝试较小的值,逐渐增加,观察算法的性能是否有所提升。在某些情况下,可能需要更多的迭代次数,特别是对于复杂的问题。
- PopulationSize(种群大小): 较大的种群通常能够提高搜索的广度,但也会增加计算成本。开始时,可以选择较小的种群大小,逐渐增加,以观察性能的变化。种群大小的选择通常取决于问题的复杂性。
- CrossoverFraction(交叉概率): 交叉概率决定了在每一代中进行交叉操作的个体比例。通常,较高的交叉概率能够促使种群更快地收敛,但可能会导致早熟收敛。建议从较小的值开始,逐渐增加,观察结果的变化。
- MutationFcn(变异函数)和MutationRate(变异概率): 变异概率影响了在每一代中进行变异操作的个体比例。不同的变异函数和概率适用于不同类型的问题。一般而言,较小的变异概率有助于保持种群的多样性。可以尝试不同的变异函数和概率,选择最适合问题的组合。
- 其他参数: 有些遗传算法可能还包含其他参数,如选择算子的权重等。这些参数的选择通常需要根据具体问题和算法的实现来进行调整。
在调整参数时,建议使用一些评估指标来监测算法的性能,如适应度值的变化、收敛速度等。同时,可以使用交叉验证等方法来验证模型的泛化性能。最终的选择应该基于问题的性质和实验结果。
适应度函数是遗传算法中的关键组成部分,它用于评估每个个体(在这里是神经网络)在解决问题上的表现。适应度函数的设计直接影响着遗传算法的性能,因为遗传算法的目标是通过进化过程筛选和改进个体,使适应度更好的个体在种群中得以保留和传递。
在遗传算法优化BP神经网络的情境中,适应度函数通常是神经网络在训练集或验证集上的性能指标,可以是均方误差、交叉熵等。适应度函数的值越小,表示神经网络的性能越好。
1.3 遗传算法优化的BP神经网络
神经网络每次训练的初识权重和阈值是随机的,会影响网络输出的精度。所以先使用遗传算法确定出最优的初识权值和阈值。
二、代码解读
2.1 数据预处理
% 关闭所有图形窗口
close all;
% 清除工作区所有变量
clear all;
% 清空命令窗口
clc;
% 从Excel文件读取数据
data = xlsread('data');
% 数据标准化(可选)
% data = zscore(data);
% 提取输入和输出数据
inputData = data(:, 2:4)';
outputData = data(:, 5:9)';
% 划分数据集为训练集和测试集
trainRatio = 0.8; % 训练集比例
testRatio = 0.2; % 测试集比例
[trainInd, testInd] = dividerand(size(inputData, 2), trainRatio, testRatio);
trainInput = inputData(:, trainInd);
trainOutput = outputData(:, trainInd);
testInput = inputData(:, testInd);
testOutput = outputData(:, testInd);
2.2 GABP
%% GA_BP
% 本部分代码演示了使用遗传算法优化BP神经网络的过程。
% 创建神经网络
hiddenLayerSize = 10; % 隐层神经元的数量
net = feedforwardnet(hiddenLayerSize, 'trainFcn', 'traingda');
% 手动设置传递函数
net.layers{1}.transferFcn = 'tansig'; % 设置隐层传递函数为双曲正切函数
net.layers{2}.transferFcn = 'purelin'; % 设置输出层传递函数为线性函数
% 禁用训练时的图形界面
net.trainParam.showWindow = false;
% 使用遗传算法确定初值权值和阈值,迭代次数20,种群数量10,交叉概率0.7,变异概率0.1
options = gaoptimset('Generations', 20, 'PopulationSize', 10, 'CrossoverFraction', 0.7, 'MutationFcn', {@mutationuniform, 0.1});
% 定义适应度函数
fitnessFunction = @(params) neuralNetworkFitness(params, trainInput, trainOutput, testInput, testOutput, hiddenLayerSize);
% 运行遗传算法
numParams = numel(net.IW{1}) + numel(net.LW{2,1}) + numel(net.b{1});
bestParams = ga(fitnessFunction, numParams, [], [], [], [], [], [], [], options);
% 从遗传算法的结果中提取权值和阈值
net.IW{1} = reshape(bestParams(1:numel(net.IW{1})), size(net.IW{1}));
net.LW{2,1} = reshape(bestParams(numel(net.IW{1})+1:numel(net.IW{1})+numel(net.LW{2,1})), size(net.LW{2,1}));
net.b{1} = reshape(bestParams(numel(net.IW{1})+numel(net.LW{2,1})+1:end), size(net.b{1}));
% 设置训练参数
net.trainParam.epochs = 1000; % 迭代次数
net.trainParam.lr = 0.01; % 学习率
% 训练神经网络
net = train(net, trainInput, trainOutput);
% 使用训练后的神经网络进行预测
predictions = net(testInput);
% 显示预测结果与实际输出的比较
figure;
plot(testOutput, '-o', 'DisplayName', '实际输出');
hold on;
plot(predictions, '-*', 'DisplayName', '预测输出');
legend('show');
xlabel('样本');
ylabel('输出值');
title('BP神经网络预测结果');
grid minor;
% 定义适应度函数
function fitness = neuralNetworkFitness(params, trainInput, trainOutput, testInput, testOutput, hiddenLayerSize)
% 创建神经网络
net = feedforwardnet(hiddenLayerSize);
% 禁用训练时的图形界面
net.trainParam.showWindow = false;
% 从参数中提取权值和阈值
net.IW{1} = reshape(params(1:numel(net.IW{1})), size(net.IW{1}));
net.LW{2,1} = reshape(params(numel(net.IW{1})+1:numel(net.IW{1})+numel(net.LW{2,1})), size(net.LW{2,1}));
net.b{1} = reshape(params(numel(net.IW{1})+numel(net.LW{2,1})+1:end), size(net.b{1}));
% 训练神经网络
trainedNet = train(net, trainInput, trainOutput);
% 使用训练后的神经网络进行预测
predictions = trainedNet(testInput);
% 计算预测结果与实际输出的适应度
% 计算预测结果与实际输出之间的平方差,作为适应度的度量
% 遗传算法的目标是最小化适应度值
fitness = sum((predictions - testOutput).^2);
fitness = sum(fitness);
end
2.3 部分函数说明
dividerand用于随机划分数据,可以方便地生成训练集和测试集,并且可以指定划分的比例。
dividerand 函数的基本用法和参数:
[trainInd, testInd] = dividerand(N, trainRatio, testRatio, valRatio)
- N: 数据集中样本的总数。
- trainRatio: 训练集占总样本数的比例。
- testRatio: 测试集占总样本数的比例。
- valRatio: 可选参数,用于指定验证集的比例。如果省略,则没有验证集。
返回值:
- trainInd: 训练集的索引。这是一个逻辑索引,对应于哪些样本被选为训练集。
- testInd: 测试集的索引。同样是逻辑索引,对应于哪些样本被选为测试集。
feedforwardnet 用于创建前馈神经网络(Feedforward Neural Network,FNN),也被称为多层感知机(Multilayer Perceptron,MLP)。前馈神经网络是一种常见的神经网络结构,具有输入层、若干隐层和输出层,信息从输入层经过隐层传递到输出层,不涉及循环连接。
feedforwardnet 函数的基本用法:
net = feedforwardnet(hiddenLayerSizes, trainFcn)
- hiddenLayerSizes: 一个包含每个隐层神经元数量的行向量。例如,
[10 8]表示两个隐层,第一个隐层有10个神经元,第二个隐层有8个神经元。可以省略该参数,默认为一个包含10个神经元的单隐层。 - trainFcn: 训练函数的名称,用于指定神经网络的训练算法。常见的训练函数包括
'trainlm'(Levenberg-Marquardt反向传播)、'traingd'(梯度下降法)等。
返回值:
- net: 创建的前馈神经网络对象。
使用示例:
hiddenLayerSizes = [10 5]; % 两个隐层,分别有10和5个神经元
trainFcn = 'trainlm'; % 使用Levenberg-Marquardt反向传播训练算法
net = feedforwardnet(hiddenLayerSizes, trainFcn);
在上面的例子中,feedforwardnet 函数被用于创建一个具有两个隐层(分别有10和5个神经元)的前馈神经网络,使用 Levenberg-Marquardt 反向传播作为训练算法。创建后,可以通过 train 函数对该神经网络进行训练。
gaoptimset用于创建一个参数结构,该结构包含了遗传算法的各种设置,例如迭代次数、种群大小、交叉概率、变异概率等。
gaoptimset 函数的基本用法:
options = gaoptimset('ParameterName1', value1, 'ParameterName2', value2, ...)
其中,ParameterName 是需要设置的参数的名称,而 value 是对应的参数值。可以设置多个参数,每个参数都有默认值,可以根据需要进行自定义。
常见的参数包括:
- ‘Generations’: 指定遗传算法的迭代次数。
- ‘PopulationSize’: 指定种群的大小,即每一代中个体的数量。
- ‘CrossoverFraction’: 指定交叉概率,即每一对个体进行交叉的概率。
- ‘MutationFcn’: 指定变异函数,控制个体基因的变异。
- 其他参数:还有许多其他参数,可以根据具体需求设置。
返回值:
- options: 包含了设置好的参数的结构体,可用于传递给遗传算法函数。
使用示例:
options = gaoptimset('Generations', 50, 'PopulationSize', 20, 'CrossoverFraction', 0.7, 'MutationFcn', {@mutationuniform, 0.1});
在上面的例子中,gaoptimset 被用于创建一个参数结构,设置了遗传算法的迭代次数为50,种群大小为20,交叉概率为0.7,并指定了变异函数为均匀变异,变异概率为0.1。创建后的 options 结构可以传递给遗传算法函数,如 ga 函数。
numel 用于返回数组中元素的总数,即数组的元素个数。numel 的名称是 “number of elements” 的缩写。
ga 函数是用于执行遗传算法(Genetic Algorithm)的主要函数。遗传算法是一种启发式搜索算法,通过模拟自然选择、交叉和变异等生物进化过程,来寻找最优解或者逼近最优解。
基本语法如下:
[x, fval] = ga(fun, nvars)
其中,fun 是适应度函数,用于评估每个个体的适应度;nvars 是决策变量的个数。
除了上述基本语法,ga 函数还支持更多的输入参数,以定制遗传算法的行为。以下是一些常见的参数:
- lb: 决策变量的下界(lower bound),是一个包含每个决策变量下界的向量。
- ub: 决策变量的上界(upper bound),是一个包含每个决策变量上界的向量。
- Aineq, bineq: 不等式约束矩阵 Aineq 和向量 bineq。
- Aeq, beq: 等式约束矩阵 Aeq 和向量 beq。
- options: 一个包含自定义选项的结构体,可以通过
gaoptimset函数创建。
返回值包括:
- x: 最优解(优化问题的决策变量)。
- fval: 最优解对应的适应度值。
使用示例:
fun = @(x) x^2; % 适应度函数,例如最小化 x^2
nvars = 1; % 决策变量的个数
[x, fval] = ga(fun, nvars);
disp(x);
disp(fval);
在上面的例子中,ga 函数用于最小化适应度函数 fun,并返回最优解 x 和对应的适应度值 fval。
reshape 用于改变数组维度的函数。它允许你将一个数组重新组织成不同维度的数组,而不改变数组中的元素顺序。reshape 的基本语法如下:
B = reshape(A, sizeB)
其中,A 是要重新组织的数组,sizeB 是一个包含新数组维度的大小的向量。新数组 B 的元素顺序与原始数组 A 保持一致。
train 函数用于训练神经网络,而 net 函数用于创建神经网络对象:
train 函数用于训练神经网络。其基本语法如下:
net = train(net, inputs, targets)
- net: 被训练的神经网络对象。
- inputs: 输入样本矩阵,每一列代表一个样本。
- targets: 目标输出样本矩阵,每一列代表对应输入样本的目标输出。
train 函数通过对神经网络进行迭代学习,不断调整权重和阈值,以使网络的输出逼近目标输出。训练过程中可以设置多个参数,例如训练的最大迭代次数、学习率等。
net 函数用于创建神经网络对象。其基本语法如下:
net = net(hiddenLayerSize, trainFcn)
- hiddenLayerSize: 包含每个隐层神经元数量的行向量,用于定义神经网络的结构。
- trainFcn: 训练函数的名称,用于指定神经网络的训练算法。
创建神经网络对象后,可以通过修改网络对象的属性,例如设置传递函数、学习率等,来定制网络的行为。
使用示例:
hiddenLayerSize = [10, 5];
trainFcn = 'traingda';
net = feedforwardnet(hiddenLayerSize, 'trainFcn', trainFcn);
在上面的例子中,net 函数被用于创建一个具有两个隐层(分别有10和5个神经元)的前馈神经网络,使用 ‘traingda’(适应性梯度下降法)作为训练算法。
网络的属性:
神经网络对象 net 具有许多属性,这些属性可以通过修改来定制神经网络的行为。以下是一些常见的 net 对象的属性:
net.numInputs: 输入层的数量。net.numLayers: 总层数(包括输入层、隐层和输出层)。net.numOutputs: 输出层的数量。net.inputs: 输入层的属性,包括输入名称、范围等。net.layers: 所有层的属性,包括每个层的权重、传递函数等。net.outputs: 输出层的属性,包括输出名称、范围等。net.biases: 所有层的偏置值。net.IW: 输入层到隐层的权重。net.LW: 隐层到隐层或隐层到输出层的权重。net.b: 隐层或输出层的偏置。net.layers{i}.transferFcn: 第 i 层的传递函数。net.trainFcn: 训练函数的名称,用于指定神经网络的训练算法。net.trainParam: 训练参数的结构体,包括学习率、最大迭代次数等。
这些属性提供了对神经网络内部结构和参数的详细控制。通过修改这些属性,你可以调整神经网络的拓扑结构、权重和训练算法等,以满足特定的问题需求。例如,可以通过修改 net.layers{i}.transferFcn 来更改特定层的传递函数,通过调整 net.trainParam 来设置训练参数。
net.trainParam 是神经网络对象 net 中的一个属性,它是一个结构体,包含了与神经网络训练相关的参数。通过修改 net.trainParam 中的参数,可以调整神经网络的训练过程。
以下是一些常见的 net.trainParam 中的参数:
net.trainParam.epochs: 训练的最大迭代次数。当达到这个迭代次数时,训练过程会停止。net.trainParam.goal: 训练的目标,即期望的性能目标。当训练误差达到或低于这个目标时,训练过程会停止。net.trainParam.lr: 学习率(Learning Rate),用于调整权重更新的步长。学习率的大小影响训练的速度和稳定性。net.trainParam.mc: 动量常数(Momentum Constant),用于考虑前一步权重更新对当前步的影响。动量有助于加速收敛。net.trainParam.max_fail: 允许连续多少次训练失败(未达到目标或性能没有改善)后终止训练。net.trainParam.min_grad: 训练过程中的梯度阈值。当梯度的大小低于该阈值时,训练过程会停止。net.trainParam.show: 控制训练过程中的显示信息。设置为 1 时显示,设置为 0 时不显示。net.trainParam.showCommandLine: 控制是否在命令行中显示训练过程的信息。net.trainParam.showWindow: 控制是否显示训练过程的图形窗口。
这些参数允许用户对神经网络的训练过程进行详细的调整和监控。例如,可以通过设置合适的学习率、动量常数和训练停止条件来优化训练过程。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!