海量数据处理数据结构之Hash与布隆过滤器

前言

随着网络和大数据时代的到来，我们如何从海量的数据中找到我们需要的数据就成为计算机技术中不可获取的一门技术，特别是近年来抖音，快手等热门短视频的兴起，我们如何设计算法来从大量的视频中获取当前最热门的视频信息呢，这就是我们今天即将谈到的Hash和布隆过滤器。以下是Hash和布隆过滤器的一些常见应用：

• 使用word文档时，如何判断某个单词是否拼写正确？
• 网络爬虫程序时，怎么让它不去爬相同的url页面(将已经爬过的url页面放到数据库中)
• 垃圾邮件过滤算法如何设计？（当多少人将同一封邮件视为垃圾邮件时，就放到数据库中，当其他人在收到相同的邮件时，直接放到垃圾邮箱中）
• 数据库缓存穿透问题如何解决?(对于redis和数据库中都不存在的数据，在服务器端使用布隆过滤器进行过滤掉，如果服务器的布隆过滤器没有过滤掉，则说明数据库可能存在，对于误判的情况，即不存在的数据判断为存在，则在redis中保存为<key,null>,这样就可以防止数据库不存在的数据对应的数据时，就不会去访问数据库了,后面还会提到，这里先提前说明下)

背景

假如我们需要从海量数据中查询某个字符串是否存在？如果让你设计一种数据结构，你会想到哪些数据结构呢？链表和数组(直接排除，查询复杂度为0(n))，二叉树(红黑树，AVL树，时间复杂度o(log（n）)，可以考虑)，平衡多叉树(B树，B+树等，时间复杂度为h.log(n),其中h为树的层高)，Hash(时间复杂度为O(1))，下面分别介绍这些数据结构

平衡二叉树

增删改查时间复杂度为O(logn) ：比如100万个节点，最多比较 20 次；10 亿个节点，最多比较 30 次；
平衡的目的时保证二叉树的左右节点的高度都差不多，这样二叉树才能保证时间复杂度为O(logn),否则最坏的情况，二叉树的时间复杂度为O(n),退化为线性表，插入数据的时候时按顺序插入的。
平衡二叉树是中序遍历有序(左子树的key<根节点的key<右子树的key)，每次比较都能保证到左子树或者右子树，每次都能排除一半的元素达到快速索引的目的.元素的比较是使用的二分查找(每次搜索都能排除一半)，使用到二分查找的结构如下图所示：

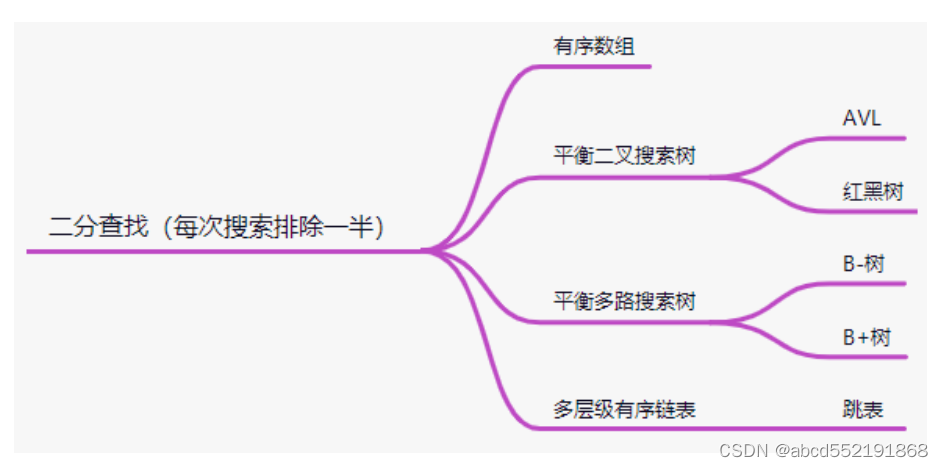
有序数组和平衡二叉搜索树使用二分查找无可厚非，对于B树和B+树而言，其实跟平衡二叉搜索树类似，只是B树的一个节点有多个KEY，每个节点有多个孩子，每个节点内的KEY都是有序的。因此在查找KEY位于哪个节点时，也使用到了二分查找，关于跳表的数据结构请参考其他博客。
如果对平衡二叉树和平衡多叉树有兴趣的同学，可以参考我的博客
1.B树和B+树的分析和实现
2.红黑树的分析与实现

散列表

前面提到的平衡二叉树的时间复杂度为O(log(n)),效率还是蛮高的，不过对于像字符串作为的key时而进行比较时，还是比较耗时的，因此有没有一种更高效的算法来完成字符串的比较呢，那就是使用散列表来完成，散列表是使用hash函数将一个key映射到一个数据表中，这样在没有冲突的情况下，根本不需要字符串的比较，只要在查询的时候，如果相应的key映射的下标中存在元素，即可完成数据的查询。
散列表是根据key计算key在表中的位置的数据结构，是 key 和其所在存储地址的映射关系；在插入数据时，需要将散列表的节点中的key和value一起存储到表中。 为什么需要存储key，这时因为在查询时，需要将查询的key和表中的key进行比较，看是否相等，如果不等，则代表这次查询失败(不等，则代表存在哈希冲突，表中的这个位置被其他key所拥有)

hash函数

映射函数 Hash(key)=addr ；hash 函数可能会把两个或两个以上的不同 key 映射到同一地址，这种情况称之为冲突（或者 hash 碰撞）；由于存在冲突情况，因此在选择hash函数时，需要满足以下2个条件，这样才能保证冲突的概率最小化和查询效率。

• 计算速度快(满足查询效率)
• 强随机分布（等概率、均匀地分布在整个地址空间），这样才能保证hash冲突的概率最小化

通常常用的哈希函数有：murmurhash1，murmurhash2，murmurhash3，siphash（redis6.0当中使?，rust等大多数语言选用的hash算法来实现hashmap），cityhash 都具备强随机分布性；测试地址如下：https://github.com/aappleby/smhasher，siphash主要 解决了字符串接近的强随机分布性，作为redis的hash算法时因为，在redis中，经常使用uid:1000和uid:1001这样的key，这2个key很接近，如果使用其他的算法，很可能都映射到同一个地址，而siphash却可以让这2个key映射到不同的地址。

负载因子

数组存储元素的个数 / 数据长度；用来形容散列表的存储密度；负载因子越小，冲突越小，负载因子越大，冲突越大；

冲突处理

不管如何优秀的hash算法，都不可避免的让不同的key映射到同一个地址，那么如何处理这样的情况，即如何处理hash冲突呢。主要有链表法和开发寻址法

链表法

引用链表来处理哈希冲突；也就是将冲突元素用链表链接起来；这也是常用的处理冲突的?
式；但是可能出现一种极端情况，冲突元素比较多，该冲突链表过长，这个时候可以将这个
链表转换为红黑树；由原来链表时间复杂度 转换为红黑树时间复杂度 ；那么判断该链表过长的依据是多少？可以采?超过 256（经验值）个节点的时候将链表结构转换为红黑树结构；

开放寻址法

将所有的元素都存放在哈希表的数组中，不使用额外的数据结构；一般使用线性探查的思路
解决；

1. 当插入新元素的时，使用哈希函数在哈希表中定位元素位置；
2. 检查数组中该槽位索引是否存在元素。如果该槽位为空，则插?，否则3；
3. 在 2 检测的槽位索引上加一定步长接着检查2； 加?定步长分为以下几种：
   1. i+1,i+2,i+3,i+4, … ,i+n
   2. i- ,i+ ,i- ,1+ , … 这两种都会导致同类 hash 聚集；也就是近似值它的hash
      值也近似，那么它的数组槽位也靠近，形成 hash 聚集；第一种同类聚集冲突在
      前，第二种只是将聚集冲突延后； 另外还可以使用双重哈希来解决上面出现hash
      聚集现象：在.net HashTable类的hash函数Hk定义如下：

Hk(key) = [GetHash(key) + k * (1 + (((GetHash(key) >> 5) 
+ 1) %(hashsize – 1)))] % hashsize

在此 (1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1))) 与 hashsize互为素数（两数互为素数表示两者没有共同的质因?）；执?了 hashsize 次探查后，哈希表中的每?个位置都有且只有?次被访问到，也就是说，对于给定的 key，对哈希表中的同?位置不会同时使? Hi 和 Hj；

布隆过滤器

既然hash的查询效率已经达到了O(1),效率已经达到了常数，那么我们需要从海量数据中(比如10亿条)查询某个字符串是否存在时是否可以使用hash来完成查询呢，其实是不可以的，虽然hash查询效率很高，也不需要比较字符串，但是需要将字符串存储到内存中，那么多条数据的字符串key存储到内存中是不现实的，那么是否有不需要字符串key的数据结构就能知道相应的元素是否存在呢？布隆过滤器的出现就是解决这个问题的。

布隆过滤器结构说明

布隆过滤器是一种概率型数据结构，它的特点是高效地插入和查询，能确定某个字符串一定不存在或者可能存在（即存在一定的误差，本来字符串key不存在，却被视为字符串存在）；
布隆过滤器不存储具体数据，所以占用空间小，查询结果存在误差，但是误差可控，同时不支持删除操作；

位图操作

在说明布隆过滤器如何实现之前，先来了解一下，如何采用一个算法将一个字符串key映射到位图中的某一位中。比如我们有一个8 * 8 的位图，另有一个字符串val(假如为"thestringkey"),采用上面或者任意的一种hash算法，比如得到 hash(val) = 173,那么如何将hash值173映射到
下面的二维位图中呢

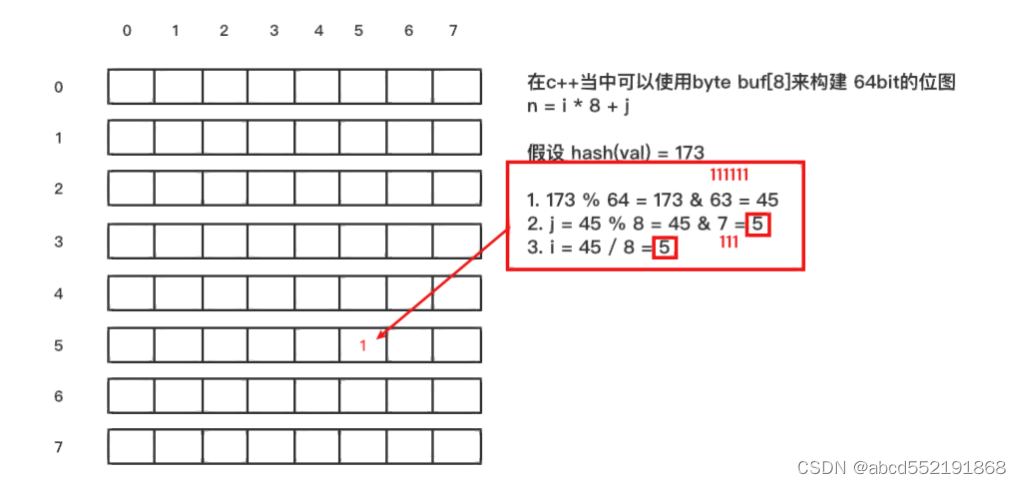
布隆过滤器原理

了解玩位图操作之后，就很容易理解布隆过滤器原理了。
当一个元素加入位图时，通过 k 个 hash 函数将这个元素映射到位图的 k 个点，并把它们置为 1；当检索时，再通过 k 个 hash 函数运算检测位图的 k 个点是否都为 1；如果有不为 1 的点，那么认为该 key 不存在；如果全部为 1，则可能存在**(这些1可能是由其他key映射的，这也是布隆过滤器存在误差的原因，什么时候使用布隆过滤器呢，在应用场景里面以缓存穿透来进行说明)**；

为什么不支持删除操作？
在位图中每个槽位只有两种状态（0 或者 1），一个槽位被设置为 1 状态，但不确定它被设
置了多少次；也就是不知道被多少个 key 哈希映射而来以及是被具体哪个 hash 函数映射而
来；

应用场景

后续在完成

应用分析

变量关系

布隆过滤器关键代码

分布式一致性 hash

总结