C++系列-第1章顺序结构-7-浮点型

在线练习:
http://noi.openjudge.cn/
https://www.luogu.com.cn/
总结
本文是C++系列博客,主要讲述浮点型的用法
浮点型
1、常量
圆周率是一个常数。计算机程序设计中有一个类似的概念是“常量”。C++语言规定,一个常量可以直接调用(如 124、3.14 等),也可以给常量取个名字用一个标识符代表它,这就是符号常量。其语法格式为:
const 类型符号常量=常量字串例如: const double PI=3.14;
习惯上,符号常量名用大写,而变量名用小写,以便于区别。使用符号常量的一般还有一下两个好处:
增加了程序的可读性。如见到 PI 就可知道它代表圆周率,定义符号常量名时应该尽量使用见名知意的常量名。
增加了程序的易改性。如程序中,只需改动一处,程序中的所有 PI都会自动全部代换,做到“一改全改”
2.实型
C++语言支持三种实型,它们是 float(单精度实型)、double(双精度实型)long double(长双精度实型)。float 在空间允许的情况下没有必要使用,都应使用 double 提高精度。
3.保留小数
如果直接使用 cout<<进行浮点数的输出,C++默认的流输出数值有效位是 6位,我们可以使用 setprecision ()来改变有效位个数。例如,
#include <iostream>
#include <iomanip>
using namespace std;
int main() {
cout<<setprecision(3)<<3.1415926;
cout<<setprecision(3)<<31.415926;
}
将输出的结果为 3.14
在实际的题目中,往往需要保留小数,而不知道整数部分的长度,我们可以将 fixed 和 setprecision ()合用,以保留小数点后有效数字的位数。
例如,
#include <iostream>
#include <iomanip>
using namespace std;
int main() {
cout<<setprecision(3)<<3.1415926<<endl;
cout<<setprecision(3)<<31.415926<<endl;
cout<<fixed<<setprecision(3)<<31.415926;
}
将输出的结果也为
整型的大小
参考:C/C++之最值limits.h(climits)和limits头文件
在limits.h/climits中,定义了INT_MAX,INT_MIN,可以直接使用
INT_MAX = 2^31-1,INT_MIN= -2^31,分别表示最大整数和最小整数。
占的位数
32位编译系统:int占四字节,与long相同。long int和int是一回事
64位编译系统:int占四字节,long占8字节,long数据范围变为:-2^63 ~ 2^63-1
注意,long long在任何平台和编译器上都已经被定义为占8个字节。
#include <iostream>
#include <climits> //limits.h
using namespace std;
int main() {
cout << "sizeof(char)" << sizeof(char) << endl;
cout << "sizeof(int) " << sizeof(int) << endl;
cout << "sizeof(long) " << sizeof(long) << endl;
cout << "sizeof(double) " << sizeof(double) << endl;
cout << "sizeof(float) " << sizeof(float) << endl;
/*
sizeof(char)1
sizeof(int) 4
sizeof(long) 4
sizeof(double) 8
sizeof(float) 4
*/
return 0;
}
输出为:
最大值
#include <iostream>
#include <climits> //limits.h
using namespace std;
int main() {
cout << "char: " << CHAR_MAX << endl;
cout << "short: " << SHRT_MAX << endl;
cout << "int: " << INT_MAX << endl;
cout << "long: " << LONG_MAX << endl;
cout << "long long: " << LLONG_MAX << endl;
/*
char: 127
short: 32767
int: 2147483647
long: 2147483647
long long: 9223372036854775807
*/
return 0;
}
输出为:
最小值
#include <iostream>
#include <climits> //limits.h
using namespace std;
int main() {
cout << "char: " << CHAR_MIN << endl;
cout << "short: " << SHRT_MIN << endl;
cout << "int: " << INT_MIN << endl;
cout << "long: " << LONG_MIN << endl;
cout << "long long: " << LLONG_MIN << endl;
/*
char: -128
short: -32768
int: -2147483648
long: -2147483648
long long: -9223372036854775808
*/
return 0;
}
输出为:
带符号与无符号
#include <iostream>
#include <climits> //limits.h
using namespace std;
int main() {
cout << "signed char_max: " << SCHAR_MAX << endl;
cout << "signed char_min: " << SCHAR_MIN << endl;
cout << "unsigned char: " << UCHAR_MAX << endl;
cout << "unsigned short: " << USHRT_MAX << endl;
cout << "unsigned int: " << UINT_MAX << endl;
cout << "unsigned long: " << ULONG_MAX << endl;
cout << "unsigned long long: " << ULLONG_MAX << endl;
/*
signed char_max: 127
signed char_min: -128
unsigned char: 255
unsigned short: 65535
unsigned int: 4294967295
unsigned long: 4294967295
unsigned long long: 18446744073709551615
*/
return 0;
}
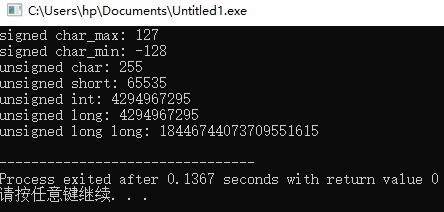
int 计算机中占4个字节,32位,是有符号数,long long ,占8个字节,64位。
浮点型的大小
在C++中,浮点型数值的范围大小取决于所使用的数据类型,以及计算机系统中的浮点数标准。C++定义了三种浮点类型:float、double和long double。这些类型分别对应着不同位数的存储空间,从而影响着数值的范围和精度。
占的位数
32位编译系统:int占四字节,与long相同。long int和int是一回事
64位编译系统:int占四字节,long占8字节,long数据范围变为:-2^63 ~ 2^63-1
注意,long long在任何平台和编译器上都已经被定义为占8个字节。
#include <iostream>
#include <climits> //limits.h
using namespace std;
int main() {
cout << "sizeof(char)" << sizeof(char) << endl;
cout << "sizeof(int) " << sizeof(int) << endl;
cout << "sizeof(long) " << sizeof(long) << endl;
cout << "sizeof(double) " << sizeof(double) << endl;
cout << "sizeof(float) " << sizeof(float) << endl;
/*
sizeof(char)1
sizeof(int) 4
sizeof(long) 4
sizeof(double) 8
sizeof(float) 4
*/
return 0;
}
输出为:

float:单精度浮点型
float:单精度浮点型,通常占用32位内存,遵循IEEE 754标准。它可以表示的数值范围大约在3.40282347E+38到1.17549E-38之间。这个范围内包括了正数、负数、零、无穷大和非数值(NaN,Not a Number)。
案例演示:
#include <iostream>
#include<limits>
using namespace std;
int main() {
float f = 1.23456789F;
cout << "The value of f is: " << f << endl;
cout << "The range of float is: " << numeric_limits<float>::max() << " to " << numeric_limits<float>::min() << endl;
return 0;
}
输出为:
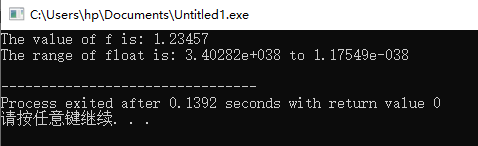
在这个例子中,f 被初始化为一个单精度浮点数,limits 头文件提供了关于浮点类型的最大值和最小值的信息。
double:双精度浮点型
double:双精度浮点型,通常占用64位内存。双精度浮点数的范围大约在1.79769313486231570E+308到2.2250738585072014E-308之间。
案例演示:
#include <iostream>
#include<limits>
using namespace std;
int main() {
double d = 1.23456789;
cout << "The value of f is: " << d << endl;
cout << "The range of float is: " << numeric_limits<double>::max() << " to " << numeric_limits<double>::min() << endl;
return 0;
}
输出为:
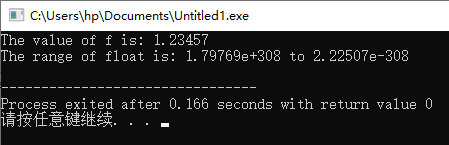
在这个例子中,d 被初始化为一个双精度浮点数。
long double:长双精度浮点型
long double:长双精度浮点型,占用大于64位的内存,具体大小取决于编译器和系统。它的范围通常比double类型更广。
案例演示:
#include <iostream>
#include<limits>
using namespace std;
int main() {
long double ld = 1.23456789L;
cout << "The value of f is: " << ld << endl;
cout << "The range of float is: " << numeric_limits<long double>::max() << " to " << numeric_limits<long double>::min() << endl;
return 0;
}
输出为:
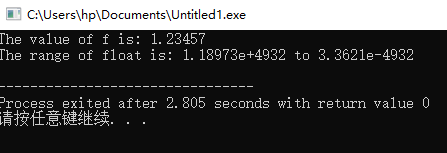
应注意的是,long double 的具体存储大小和范围可能因平台和编译器而异,所以上面的代码仅提供一个示例。
浮点数的表示方式遵循IEEE 754标准,该标准定义了浮点数的存储格式,包括符号位、指数位和尾数位。在C++中,浮点数的范围和精度受这些标准规则的限制,同时也受到编译器和平台的影响。
浮点数的精度计算
开门见山
float范围:
最小负数-2*2^127
最大负数-1*2^(-126),0
最小正数 1*2^(-126)
最大正数2*2^(127)。
double范围:
负数:(-1.7976931348623157E+308,-4.94065645841246544E-324);
零:0 ;
正数:(4.94065645841246544E-324,1.7976931348623157E+308)。
即绝对值为0和2^1022——2^1024。
精度:
float和double的精度是由尾数的位数来决定的;
浮点数在内存中是按科学计数法来存储的,其整数部分始终是一个隐含着的“1”,由于它是不变的,故不能对精度造成影响;
float:2^23 =8388608,共七位,意味着最多能有7位有效数字,但绝对能保证的为6位,也即float的精度为6~7位有效数字;
double:2^52 = 4503599627370496,一共16位,同理,double的精度为15~16位。
原因
float:1bit(符号位)+8bits(指数位)+23bits(尾数位);
double:1bit(符号位)+ 11bits(指数位)+ 52bits(尾数位)。
以float为例,阶码(指数)用移码来表示,8位移码(偏移量为127) 本来应该可以表示-128-127,但是全0和全1被用来 表示特殊状态的指数 ,所以为-126-127(无符号8位表示0-255,去除全0和1后是1-254,减去偏移量127,就是-126-127)。 这里为什么要使用127来作为偏移量,若使用128 则8位移码表示范围-127~126,由于表示一个大的正数 比一个小的负数更加重要,所以127作为偏移量比较合适。
现在可以计算其表示范围了:
尾数部分的取值范围[1,2),所以最
小负数-2*2^127
最大负数-1*2^(-126)
最小正数 1*2^(-126)
最大正数2*2^(127)
以float类型为例,我们可以根据IEEE 754标准来计算其最大数值和最大精度。
最大数值
float类型的最大数值是由其表示的精度和存储空间决定的。对于32位的float类型,其最大数值是:
- 符号位:1位
- 指数位:8位
- 尾数位:23位
根据IEEE 754标准,float类型的指数位采用偏移表示法,即实际的指数值是存储的指数值减去一个偏移量。对于float类型,这个偏移量是127。因此,最大的指数值为2^8 - 1 = 255,但由于偏移量是127,所以实际的指数范围是从-126到127。
对于最大数值,我们考虑最大的正指数(即指数为127),并且尾数位全为1的情况。这种情况下,最大数值为:
(-1)^0 * 2^(127 - 127) * 1.1111111...1111111
由于指数为0,这个数值实际上是1.1111111…1111111(23个1)乘以2的0次方,即1。但是,由于IEEE 754标准中有一个隐藏的1,实际上这个最大数值是:
(-1)^0 * 2^(127 - 127) * 1.1111111...1111111 * 2^(-23)
这个隐藏的1是用来保证浮点数的表示不会比实际的整数小,同时也是IEEE 754标准中规定的一部分。因此,最大数值实际上是:
1 + 2^(-23)
这个数值是float类型的最大正数值,其值为3.40282347E+38。
最大精度
最大精度是指float类型能够表示的最小的数值变化。由于float类型的尾数位有23位,因此最大精度是2的-23次方,即:
2^(-23)
这个数值是非常小的,表示float类型能够表示的精度非常高。例如,如果有一个float变量存储了一个数值,那么这个数值的实际值可以在其基础上加上或减去最大精度而不改变可观察到的值。
综上所述,float类型的最大数值是3.40282347E+38,最大精度是2的-23次方。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- gmail邮箱发送邮件 java
- ECMAScript简介及特性
- 中兴通讯5G-A场景突破成果显著,获得行业高度认可
- 小信砍柴的题解
- 提升开发效率,Fiddler Everywhere for Mac助您解决网络调试难题
- 用Xshell连接虚拟机的Ubuntu20.04系统记录。虚拟机Ubuntu无法上网。本机能ping通虚拟机,反之不能。互ping不通
- leetcode-2645 构造有效字符串的最小插入数
- apache poi_5.2.5 实现对表格单元格的自定义变量名进行图片替换
- UVeiw 组件的使用(更多自定义案例和解决方案),Vue3 +ts 版本 #Selected组件 #Vue 3 # Ts
- YAPI:现代化的接口管理平台