模型系列:聚类_五个聚类算法比较综述
介绍
聚类是最常用的无监督学习形式之一。它可以自动发现数据中的自然分组。
聚类对于探索你对其一无所知的数据尤其有用。你可能会发现你从未想过的联系。聚类还可以作为一种特征工程的方法,可以将现有和新的示例映射和标记为属于数据中已识别的聚类之一。
一些典型的实际应用包括欺诈检测、图书馆中的图书分类或市场营销中的客户细分。
1. 聚类算法的类型
有许多可供选择的聚类算法。探索一系列聚类算法和不同的配置是一个好主意。找出适合给定数据的最佳聚类算法可能需要一些时间,但一旦找到,您将获得对数据的宝贵洞察。
基于质心的
-
这些类型的算法根据数据中的多个质心将数据点分开。每个数据点根据与质心的平方距离被分配到一个簇中。
-
这是最常用的聚类类型。K-Means算法是基于质心的聚类算法之一。其中k是簇的数量,是该算法的超参数。
基于层次的(基于连接的)
-
这个想法基于对象与附近对象的关系比与远离的对象的关系更密切的核心思想。
-
它构建了一个簇的树,所以一切都是自上而下组织的。最初,每个数据点被视为一个单独的簇。在每次迭代中,相似的簇与其他簇合并,直到形成一个簇或K个簇。
基于密度的
-
数据根据数据点高浓度区域周围的低浓度区域进行分组。基本上,该算法找到了数据点密集的地方,并将其称为簇。
-
簇可以是任何形状。您不受预期条件的限制。
-
此类型下的聚类算法不会尝试将离群值分配给簇,因此它们会被忽略。
基于分布的
-
这是一种聚类模型,我们将根据数据可能属于相同分布的概率来拟合数据。
-
建立了一个中心点。随着数据点与中心的距离增加,它属于该簇的概率减小。
-
该模型在合成数据和不同大小的簇上效果良好。
-
该方法容易过拟合,除非对模型复杂性加以约束。更复杂的模型通常能更好地解释数据,这使得选择适当的模型复杂性变得困难。
2. 设置
2.1 数据集
我决定使用7个数据集。其中六个用于练习可视化,一个用于解决真实数据问题。
练习数据集:
https://www.kaggle.com/datasets/joonasyoon/clustering-exercises
真实数据集:
https://www.kaggle.com/datasets/shrutipandit707/onlineretaildata
2.2 导入库
# 导入必要的库
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
from collections import Counter
%matplotlib inline
2.3 导入数据
# 导入所需的库
import pandas as pd
# 读取数据文件
blob_df = pd.read_csv("../input/clustering-exercises/blob.csv") # 读取blob.csv文件并将数据存储在blob_df中
dart_df = pd.read_csv("../input/clustering-exercises/dart.csv") # 读取dart.csv文件并将数据存储在dart_df中
outliers_df = pd.read_csv("../input/clustering-exercises/outliers.csv") # 读取outliers.csv文件并将数据存储在outliers_df中
spiral2_df = pd.read_csv("../input/clustering-exercises/spiral2.csv") # 读取spiral2.csv文件并将数据存储在spiral2_df中
basic2_df = pd.read_csv("../input/clustering-exercises/basic2.csv") # 读取basic2.csv文件并将数据存储在basic2_df中
boxes3_df = pd.read_csv("../input/clustering-exercises/boxes3.csv") # 读取boxes3.csv文件并将数据存储在boxes3_df中
raw_df = pd.read_csv("../input/onlineretaildata/Online_Retail.csv", encoding='unicode_escape') # 读取Online_Retail.csv文件并将数据存储在raw_df中,使用unicode_escape编码解决编码问题
2.4 一些可视化展示
# 创建子图
fig, axes = plt.subplots(nrows=2, ncols=3,figsize=(13,13))
# 设置整个图的标题
fig.suptitle('EXERCISE DATA SETS\n', size = 18)
# 在第一个子图中绘制散点图,x轴为blob_df的x列,y轴为blob_df的y列,颜色根据blob_df的color列确定,点的大小为10,颜色映射为"Set3"
axes[0,0].scatter(blob_df['x'], blob_df['y'], c=blob_df['color'], s=10, cmap = "Set3")
# 设置第一个子图的标题
axes[0,0].set_title("Blob");
# 在第二个子图中绘制散点图,x轴为dart_df的x列,y轴为dart_df的y列,颜色根据dart_df的color列确定,点的大小为10,颜色映射为"Set3"
axes[0,1].scatter(dart_df['x'], dart_df['y'], c=dart_df['color'], s=10, cmap = "Set3")
# 设置第二个子图的标题
axes[0,1].set_title("Dart");
# 在第三个子图中绘制散点图,x轴为basic2_df的x列,y轴为basic2_df的y列,颜色根据basic2_df的color列确定,点的大小为10,颜色映射为"Set3"
axes[0,2].scatter(basic2_df['x'], basic2_df['y'], c=basic2_df['color'], s=10, cmap = "Set3")
# 设置第三个子图的标题
axes[0,2].set_title("Basic");
# 在第四个子图中绘制散点图,x轴为outliers_df的x列,y轴为outliers_df的y列,颜色根据outliers_df的color列确定,点的大小为10,颜色映射为"Set3"
axes[1,0].scatter(outliers_df['x'], outliers_df['y'], c=outliers_df['color'], s=10, cmap = "Set3")
# 设置第四个子图的标题
axes[1,0].set_title("Outliers");
# 在第五个子图中绘制散点图,x轴为spiral2_df的x列,y轴为spiral2_df的y列,颜色根据spiral2_df的color列确定,点的大小为10,颜色映射为"Set3"
axes[1,1].scatter(spiral2_df['x'], spiral2_df['y'], c=spiral2_df['color'], s=10, cmap = "Set3")
# 设置第五个子图的标题
axes[1,1].set_title("Spiral");
# 在第六个子图中绘制散点图,x轴为boxes3_df的x列,y轴为boxes3_df的y列,颜色根据boxes3_df的color列确定,点的大小为10,颜色映射为"Set3"
axes[1,2].scatter(boxes3_df['x'], boxes3_df['y'], c=boxes3_df['color'], s=10, cmap = "Set3")
# 设置第六个子图的标题
axes[1,2].set_title("Boxes");
# 调整子图的布局
plt.tight_layout()

2.5 特征工程
做聚类之前有一些准备工作。
# 对数据框进行描述性统计分析,包括所有列的统计信息
raw_df.describe(include='all')
| InvoiceNo | StockCode | Description | Quantity | InvoiceDate | UnitPrice | CustomerID | Country | |
|---|---|---|---|---|---|---|---|---|
| count | 541909 | 541909 | 540455 | 541909.000000 | 541909 | 541909.000000 | 406829.000000 | 541909 |
| unique | 25900 | 4070 | 4223 | NaN | 23260 | NaN | NaN | 38 |
| top | 573585 | 85123A | WHITE HANGING HEART T-LIGHT HOLDER | NaN | 31-10-2011 14:41 | NaN | NaN | United Kingdom |
| freq | 1114 | 2313 | 2369 | NaN | 1114 | NaN | NaN | 495478 |
| mean | NaN | NaN | NaN | 9.552250 | NaN | 4.611114 | 15287.690570 | NaN |
| std | NaN | NaN | NaN | 218.081158 | NaN | 96.759853 | 1713.600303 | NaN |
| min | NaN | NaN | NaN | -80995.000000 | NaN | -11062.060000 | 12346.000000 | NaN |
| 25% | NaN | NaN | NaN | 1.000000 | NaN | 1.250000 | 13953.000000 | NaN |
| 50% | NaN | NaN | NaN | 3.000000 | NaN | 2.080000 | 15152.000000 | NaN |
| 75% | NaN | NaN | NaN | 10.000000 | NaN | 4.130000 | 16791.000000 | NaN |
| max | NaN | NaN | NaN | 80995.000000 | NaN | 38970.000000 | 18287.000000 | NaN |
# 删除指定列
raw_df.drop(['StockCode', 'InvoiceDate','Description','Country'],axis = 1, inplace =True)
# 输出处理后的数据
print(raw_df)
# 打印出原始数据中"Quantity"列的最小值
print(raw_df["Quantity"].min())
# 打印出原始数据中"UnitPrice"列的最小值
print(raw_df["UnitPrice"].min())
-80995
-11062.06
负值可能意味着有退货。这对于电子商务来说是一个重要因素,但是对于这项研究,让我们只保留没有退货的交易(我们的目标是介绍和比较不同的聚类方法)。
# 从原始数据框中筛选出数量大于0的数据
df = raw_df.loc[raw_df["Quantity"] > 0]
# 从筛选后的数据框中再次筛选出单价大于0的数据
df = df.loc[df["UnitPrice"] > 0]
# 打印DataFrame中"Quantity"列的最小值
print(df["Quantity"].min())
# 打印DataFrame中"UnitPrice"列的最小值
print(df["UnitPrice"].min())
1
0.001
# 创建一个新的列Total,用于存储每个产品的总金额
df["Total"] = df["Quantity"] * df["UnitPrice"]
# 删除数据框中的'Quantity'和'UnitPrice'列
df.drop(['Quantity', 'UnitPrice'], axis=1, inplace=True)
# 检查数据中的缺失值
df.isnull().sum()
InvoiceNo 0
CustomerID 132220
Total 0
dtype: int64
# 删除具有缺失值的customerId列
df.dropna(axis=0, inplace=True)
# axis=0表示按行删除,inplace=True表示在原始DataFrame上进行修改
创建新特征:
- 频率:交易总数
- 金额:交易总金额
# 对数据框df按照'CustomerID'进行分组,计算每个顾客的'Total'总和
Amount = df.groupby('CustomerID')['Total'].sum()
# 重置索引,将'CustomerID'变为列
Amount = Amount.reset_index()
# 将列名改为'CustomerID'和'Amount'
Amount.columns=['CustomerID','Amount']
# 对数据框df按照'CustomerID'进行分组,计算每个顾客的'InvoiceNo'计数
Frequency=df.groupby('CustomerID')['InvoiceNo'].count()
# 重置索引,将'CustomerID'变为列
Frequency=Frequency.reset_index()
# 将列名改为'CustomerID'和'Frequency'
Frequency.columns=['CustomerID','Frequency']
# 将Amount和Frequency两个数据框按照'CustomerID'进行内连接合并
df1 = pd.merge(Amount, Frequency, on='CustomerID', how='inner')
# 显示合并后的前几行数据
df1.head()
| CustomerID | Amount | Frequency | |
|---|---|---|---|
| 0 | 12346.0 | 77183.60 | 1 |
| 1 | 12347.0 | 4310.00 | 182 |
| 2 | 12348.0 | 1797.24 | 31 |
| 3 | 12349.0 | 1757.55 | 73 |
| 4 | 12350.0 | 334.40 | 17 |
# 删除 'CustomerID' 列
df1.drop(['CustomerID'], axis=1, inplace=True) # 使用drop方法删除指定列,axis=1表示按列删除,inplace=True表示在原DataFrame上进行修改
2.6 异常值检测
# 使用describe函数对df1进行描述性统计分析
# 参数include='all'表示包括所有数据类型的统计结果
df1.describe(include='all')
| Amount | Frequency | |
|---|---|---|
| count | 4338.000000 | 4338.000000 |
| mean | 2054.266460 | 91.720609 |
| std | 8989.230441 | 228.785094 |
| min | 3.750000 | 1.000000 |
| 25% | 307.415000 | 17.000000 |
| 50% | 674.485000 | 41.000000 |
| 75% | 1661.740000 | 100.000000 |
| max | 280206.020000 | 7847.000000 |
# 创建一个包含1行2列的图表,并设置图表的大小为6x6
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(6,6))
# 设置整个图表的标题为"Outliers",并设置标题的字体大小为25
fig.suptitle('Outliers\n', size=25)
# 在第一个子图中绘制一个箱线图,数据为df1['Amount'],颜色使用'Spectral'调色板,同时设置子图的标题为"Amount"
sns.boxplot(ax=axes[0], data=df1['Amount'], palette='Spectral').set_title("Amount")
# 在第二个子图中绘制一个箱线图,数据为df1['Frequency'],颜色使用'Spectral'调色板,同时设置子图的标题为"Frequency"
sns.boxplot(ax=axes[1], data=df1['Frequency'], palette='Spectral').set_title("Frequency")
# 调整子图的布局,使得子图之间没有重叠
plt.tight_layout()

看起来我们在异常值方面存在着重大问题。
异常值检测模型选择
- 分布不是正态分布
- 分布高度倾斜
- 我们有巨大的异常值
孤立森林不假设正态分布,能够在多维度水平上检测异常值。孤立森林也具有计算效率高的特点。该算法基于这样一个原则,即异常值是少数且不同的观测值,这应该使得它们更容易被识别。这就是为什么我选择孤立森林。
有关异常值检测方法,请参见:
https://www.kaggle.com/code/marcinrutecki/outlier-detection-methods
# 导入IsolationForest模块
from sklearn.ensemble import IsolationForest
# 复制df1数据框到df2
df2 = df1.copy()
# 创建IsolationForest模型,设置参数n_estimators为150,max_samples为'auto',contamination为0.1,max_features为1.0
model = IsolationForest(n_estimators=150, max_samples='auto', contamination=float(0.1), max_features=1.0)
# 使用模型对数据进行训练
model.fit(df2)
/opt/conda/lib/python3.7/site-packages/sklearn/base.py:451: UserWarning: X does not have valid feature names, but IsolationForest was fitted with feature names
"X does not have valid feature names, but"
IsolationForest(contamination=0.1, n_estimators=150)
# 给df添加'scores'和'anomaly'列
scores = model.decision_function(df2) # 使用模型的decision_function方法计算每个样本的异常分数
anomaly = model.predict(df2) # 使用模型的predict方法预测每个样本的异常标签
df2['scores'] = scores # 将异常分数添加到df的'scores'列
df2['anomaly'] = anomaly # 将异常标签添加到df的'anomaly'列
anomaly = df2.loc[df2['anomaly'] == -1] # 从df中筛选出异常样本
anomaly_index = list(anomaly.index) # 获取异常样本的索引列表
print('Total number of outliers is:', len(anomaly)) # 打印异常样本的总数
# 以上代码的作用是使用一个模型对数据集df2进行异常检测,并将异常分数和异常标签添加到df2中。
# 首先,使用模型的decision_function方法计算每个样本的异常分数,并使用模型的predict方法预测每个样本的异常标签。
# 然后,将异常分数添加到df2的'scores'列,将异常标签添加到df2的'anomaly'列。
# 接着,从df2中筛选出异常样本,并将其索引保存在anomaly_index列表中。
# 最后,打印异常样本的总数。
Total number of outliers is: 434
df2 = df2.drop(anomaly_index, axis = 0).reset_index(drop=True)
print(df2.head())
# 创建一个包含1行2列的图表,大小为6x6
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(6,6))
# 设置图表的标题
fig.suptitle('Outliers\n', size = 25)
# 在第一个子图中绘制箱线图,数据为df2['Amount'],颜色使用'Spectral'调色板,设置标题为"Amount"
sns.boxplot(ax=axes[0], data=df2['Amount'], palette='Spectral').set_title("Amount")
# 在第二个子图中绘制箱线图,数据为df2['Frequency'],颜色使用'Spectral'调色板,设置标题为"Frequency"
sns.boxplot(ax=axes[1], data=df2['Frequency'], palette='Spectral').set_title("Frequency")
# 调整子图的布局,使其紧凑显示
plt.tight_layout()

我们可以看到孤立森林算法表现不错!
# 删除不再需要的列
df.drop(['scores', 'anomaly'], axis=1, inplace=True)
2.7 数据伸缩
# 导入StandardScaler类
from sklearn.preprocessing import StandardScaler
# 创建StandardScaler对象
scaler = StandardScaler()
# 使用StandardScaler对象对df2进行标准化处理,并将结果保存到df3中
df3 = scaler.fit_transform(df2)
3. 确定最佳聚类数
选择最佳聚类数是将聚类算法应用于数据集的关键,例如k-means聚类,它要求用户指定要生成的聚类数k。这是一个相当任意的过程,也是执行聚类分析的最薄弱环节之一。
肘部法和轮廓法之间的主要区别在于肘部法仅计算欧几里得距离,而轮廓法则考虑了方差、偏度、高低差等变量。
根据图表呈现的细节,肘部法/SSE图和轮廓法可以互换使用。
3.1 肘部法则
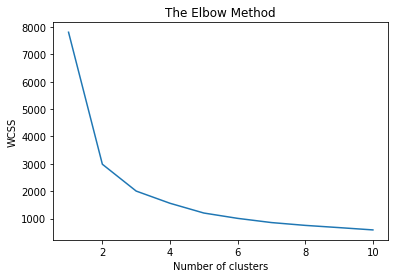
肘部法则是一种启发式方法,用于确定数据集中的聚类数量。该方法包括绘制解释的变异性作为聚类数量的函数,并选择曲线的肘部作为要使用的聚类数量。
肘部法则是在K-means聚类中找到最佳’K’的图形表示。它通过找到WCSS(簇内平方和)即簇中点与簇质心之间的平方距离之和来工作。
可以将最佳聚类数量定义如下:
- 对于不同的k值计算聚类算法(例如,k-means聚类)。例如,通过将k从1变化到10个簇。
- 对于每个k,计算总的簇内平方和(WSS)。
- 根据聚类数量k绘制wss曲线。
- 图中弯曲点(肘部)的位置通常被认为是适当的聚类数量的指示器。
# 导入KMeans聚类算法
from sklearn.cluster import KMeans
# 创建一个空列表,用于存储每个簇内平方和的值
wcss = []
# 循环1到10,分别计算每个簇内平方和的值,并将其添加到wcss列表中
for i in range(1, 11):
# 创建KMeans聚类算法对象,设置聚类数为i,初始化方式为k-means++,随机种子为42
kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
# 使用KMeans算法对数据进行聚类
kmeans.fit(df3)
# 将每个簇内平方和的值添加到wcss列表中
wcss.append(kmeans.inertia_)
# 绘制聚类数与簇内平方和的关系图
plt.plot(range(1, 11), wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()
# 导入KMeans类和KElbowVisualizer类
from yellowbrick.cluster import KElbowVisualizer
model = KMeans() # 创建一个KMeans对象
# 创建一个KElbowVisualizer对象
# k是聚类簇的数量范围
# timings参数设置为True,以便显示训练时间
visualizer = KElbowVisualizer(model, k=(2,30), timings= True)
# 将数据拟合到可视化器中
visualizer.fit(df3)
# 显示可视化结果
visualizer.show()

<AxesSubplot:title={'center':'Distortion Score Elbow for KMeans Clustering'}, xlabel='k', ylabel='distortion score'>
3.2 Silhouette方法
平均轮廓法用于衡量聚类的质量,即确定每个对象在其聚类中的表现如何。较高的平均轮廓宽度表示较好的聚类。最佳的聚类数k是在可能的k值范围内最大化平均轮廓的数值(Kaufman和Rousseeuw,1990)。
算法的计算步骤如下:
- 对不同的k值计算聚类算法(例如k-means聚类)。
- 对于每个k值,计算观测值的平均轮廓(avg.sil)。
- 根据聚类数k绘制avg.sil的曲线。
- 最大值的位置被认为是适当的聚类数。
轮廓分数的取值范围为[-1, 1]。
轮廓分数为1表示聚类非常密集且分离良好。分数为0表示聚类重叠。分数小于0表示属于聚类的数据可能是错误/不正确的。
# 导入所需的库
from sklearn import datasets
from sklearn.metrics import silhouette_score
# 实例化KMeans模型,设置聚类数为5,随机种子为42
km = KMeans(n_clusters=5, random_state=42)
# 使用KMeans模型对数据进行拟合和预测
km.fit_predict(df3)
# 计算轮廓系数
score = silhouette_score(df3, km.labels_, metric='euclidean')
# 打印轮廓系数的平均得分
print('Silhouetter Average Score: %.3f' % score)
Silhouetter Average Score: 0.476
# 导入需要的库
from yellowbrick.cluster import SilhouetteVisualizer
# 创建一个图表和子图
fig, ax = plt.subplots(3, 2, figsize=(13,8))
# 设置图表标题
fig.suptitle('2-7个聚类的轮廓分析', size = 18)
# 调整子图布局
plt.tight_layout()
# 遍历每个聚类数
for i in [2, 3, 4, 5, 6, 7]:
'''
创建一个具有不同聚类数的KMeans实例
'''
km = KMeans(n_clusters=i, init='k-means++', n_init=10, max_iter=100, random_state=42)
# 将子图分为2行3列,获取当前子图的位置
q, mod = divmod(i, 2)
'''
创建一个带有KMeans实例的SilhouetteVisualizer实例
拟合可视化器
'''
visualizer = SilhouetteVisualizer(km, colors='yellowbrick', ax=ax[q-1][mod])
visualizer.fit(df3)

选择在这里并不那么明显,原因如下:
- 存在5-7个聚类的平均轮廓分数低于平均水平的簇。
- 轮廓图的大小波动较大。
- 大小的波动不相似,但对于6和7个聚类来说更好。
- 表示每个聚类的轮廓图的厚度也是一个决定因素。不幸的是,我们有一个聚类的厚度明显大于其他聚类。
3.3 系统树图
这种技术是特定于凝聚层次聚类方法的。该方法首先将每个点视为一个单独的聚类,并根据它们之间的距离以层次方式将点与聚类连接起来。为了获得层次聚类的最佳聚类数,我们使用了一个称为系统树图的树状图,它显示了聚类的合并或分裂的顺序。
# 导入所需的库
import scipy.cluster.hierarchy as sch
from matplotlib import pyplot
# 创建一个图形窗口,设置大小为12x5
pyplot.figure(figsize=(12, 5))
# 使用ward方法计算数据集的层次聚类,并生成树状图
dendrogram = sch.dendrogram(sch.linkage(df3, method='ward'))
# 设置图形的标题为"Dendrogram"
plt.title('Dendrogram')
# 设置y轴的标签为"Euclidean distances"
plt.ylabel('Euclidean distances')
# 显示图形
plt.show()

4. K-Means
K-Means聚类可能是最广为人知的聚类算法,它将示例分配到聚类中,以尽量减少每个聚类内的方差。
它是一种基于质心的算法,也是最简单的无监督学习算法。
该算法试图最小化聚类内数据点的方差。这也是大多数人接触无监督机器学习的方式。
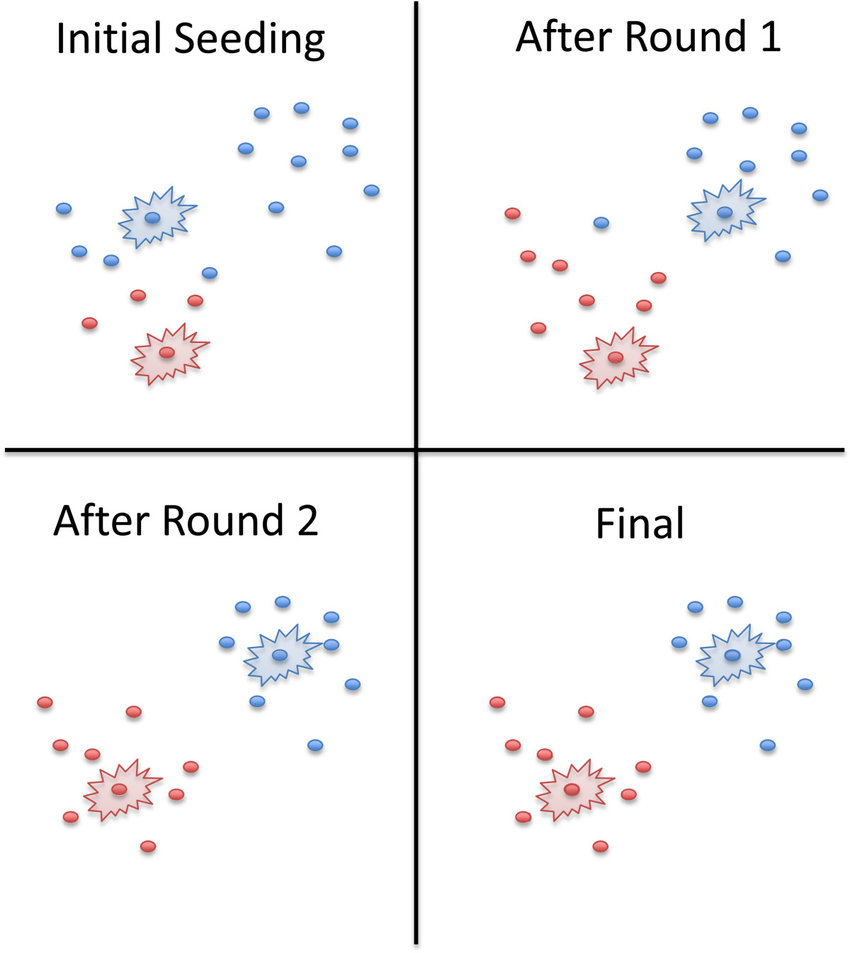
K-means++(sklearn中K-Means的默认init参数)是用来克服k-means算法的缺点的算法。其目标是通过随机分配第一个质心,然后根据最大平方距离选择其余质心来扩散初始质心。其思想是尽可能将质心推开。
尽管K-means++中的初始化计算成本比标准K-means算法更高,但对于K-means++来说,收敛到最优解的运行时间大大缩短。这是因为最初选择的质心很可能已经位于不同的聚类中。
4.1 K-Means的优缺点
K-Means是一种常见的聚类算法,它具有以下优点和缺点:
优点:
- 简单易懂,易于实现。
- 可以处理大量数据。
- 可以适用于不同类型的数据,如数值型、离散型等。
- 可以快速收敛。
缺点:
- 需要预先指定聚类数量,如果数量不正确,可能会导致聚类效果不佳。
- 对于不同形状、大小、密度的聚类效果不佳。
- 对于噪声和异常值敏感。
- 对于初始聚类中心的选择敏感,可能会导致陷入局部最优解。
K-Means聚类的优点:
- 简单 - 它易于实现
- 高性能 - K-Means聚类技术在计算成本方面快速高效
- 易于解释 - K-Means返回的聚类可以很容易地解释和可视化
- 适用于大数据集 - 尽管聚类算法通常较慢,但k-means算法相对较快,因此对于大数据集非常有效。
K-Means聚类的缺点:
- 假设球形密度 - 这意味着k-means聚类在聚类自然具有不规则形状的情况下表现不佳。这是一个相对严格的假设。
- 对比例敏感 - 如果其中一个变量的比例远大于其他变量,那么该变量对计算的距离将产生过大的影响。这意味着我们通常需要在使用k-means聚类之前重新缩放数据。
- 难以融入分类变量 - K-means适用于所有特征都是数值型的情况。如果有一些分类特征,可以通过一些方法使数据适应,但一般来说,大多数特征应该是数值型的。
- 对异常值敏感 - K-Means没有异常值检测方法。离群值可能会影响质心的位置,或者离群值可能会形成自己的簇而不被忽略。
- 对初始化条件敏感 - K-means聚类对用于初始化算法的起始条件(如种子的选择或数据点的顺序)敏感。如果我们在选择起始点时运气不好,产生的聚类可能会任意糟糕。这个问题可以通过一种称为k-means++的变体来解决(sklearn的默认初始化方法)。
- 必须选择聚类的数量 - K-means聚类需要事先指定将创建的聚类数量。选择正确的’k’值是一个具有挑战性的模型选择问题。
- 在高维数据中效果不佳 - 该算法依赖于欧氏距离,在高维度下效果较差。如果有许多潜在特征,我们应该考虑在创建聚类之前对数据应用特征选择或降维算法。
- 算法是随机的 - 这意味着我们可以在同一数据集上多次运行它并得到不同的答案。这对许多应用来说是一个大问题。
- k-means只能分离更或多或少线性可分的聚类 - 如果您的聚类是基于到原点的距离,k-means将无法识别它们。我们可以通过切换到极坐标来解决这个问题。
避免k-means算法中初始化敏感性问题的方法:
-
重复k-means - 该算法被重复执行。通过初始化质心并形成聚类,以获得最小的簇内距离和较大的簇间距离。
-
K-Means++ - 一种智能质心初始化技术。只有一个质心是随机初始化的,其他质心被选择得离初始质心非常远。这样可以加快收敛速度,并降低质心初始化不良的可能性。sklearn的默认初始化方法。K means++提供了相对更好的结果。
4.2 K-Means的变种
k-means算法的一些变体:
- k-medians聚类 - 在每个维度上使用中位数(而不是均值)。
- k-medoids(围绕中心点的分区) - 使用中心点代替均值,并最小化任意距离函数的距离总和。
- 模糊C-Means聚类 - k-means的软版本,其中每个数据点对每个聚类具有模糊的隶属度。
- k-means++ - 带有更智能的质心初始化的标准k-means算法(sklearn的默认初始化)。
4.3 在数据集上训练K-Means模型
# 复制数据集
# 复制df3数据集到df_kmeans
df_kmeans = df3.copy()
# 复制blob_df数据集到df_blob_kmeans
df_blob_kmeans = blob_df.copy()
# 复制dart_df数据集到df_dart_kmeans
df_dart_kmeans = dart_df.copy()
# 复制basic2_df数据集到df_basic_kmeans
df_basic_kmeans = basic2_df.copy()
# 复制outliers_df数据集到df_outliers_kmeans
df_outliers_kmeans = outliers_df.copy()
# 复制spiral2_df数据集到df_spiral2_kmeans
df_spiral2_kmeans = spiral2_df.copy()
# 复制boxes3_df数据集到df_boxes3_kmeans
df_boxes3_kmeans = boxes3_df.copy()
# 从数据框中删除名为'color'的列
df_blob_kmeans.drop(['color'], axis=1, inplace=True) # 在df_blob_kmeans数据框中删除名为'color'的列
df_dart_kmeans.drop(['color'], axis=1, inplace=True) # 在df_dart_kmeans数据框中删除名为'color'的列
df_basic_kmeans.drop(['color'], axis=1, inplace=True) # 在df_basic_kmeans数据框中删除名为'color'的列
df_outliers_kmeans.drop(['color'], axis=1, inplace=True) # 在df_outliers_kmeans数据框中删除名为'color'的列
df_spiral2_kmeans.drop(['color'], axis=1, inplace=True) # 在df_spiral2_kmeans数据框中删除名为'color'的列
df_boxes3_kmeans.drop(['color'], axis=1, inplace=True) # 在df_boxes3_kmeans数据框中删除名为'color'的列
# 使用KMeans算法进行聚类,将数据分为6个簇,使用k-means++初始化方法,随机种子为42
kmeans = KMeans(n_clusters = 6, init = 'k-means++', random_state = 42)
# 对数据进行聚类,并返回每个样本所属的簇的索引
y_kmeans = kmeans.fit_predict(df_kmeans)
# 使用KMeans算法进行聚类,将数据分为4个簇,使用k-means++初始化方法,随机种子为42
kmeans_blob = KMeans(n_clusters = 4, init = 'k-means++', random_state = 42)
# 对数据进行聚类,并返回每个样本所属的簇的索引
y_kmeans_blob = kmeans_blob.fit_predict(df_blob_kmeans)
# 使用KMeans算法进行聚类,将数据分为2个簇,使用k-means++初始化方法,随机种子为42
kmeans_dart = KMeans(n_clusters = 2, init = 'k-means++', random_state = 42)
# 对数据进行聚类,并返回每个样本所属的簇的索引
y_kmeans_dart = kmeans_dart.fit_predict(df_dart_kmeans)
# 使用KMeans算法进行聚类,将数据分为5个簇,使用k-means++初始化方法,随机种子为42
kmeans_basic = KMeans(n_clusters = 5, init = 'k-means++', random_state = 42)
# 对数据进行聚类,并返回每个样本所属的簇的索引
y_kmeans_basic = kmeans_basic.fit_predict(df_basic_kmeans)
# 使用KMeans算法进行聚类,将数据分为3个簇,使用k-means++初始化方法,随机种子为42
kmeans_outliers = KMeans(n_clusters = 3, init = 'k-means++', random_state = 42)
# 对数据进行聚类,并返回每个样本所属的簇的索引
y_kmeans_outliers = kmeans_outliers.fit_predict(df_outliers_kmeans)
# 使用KMeans算法进行聚类,将数据分为2个簇,使用k-means++初始化方法,随机种子为42
kmeans_spiral2 = KMeans(n_clusters = 2, init = 'k-means++', random_state = 42)
# 对数据进行聚类,并返回每个样本所属的簇的索引
y_kmeans_spiral2 = kmeans_spiral2.fit_predict(df_spiral2_kmeans)
# 使用KMeans算法进行聚类,将数据分为12个簇,使用k-means++初始化方法,随机种子为42
kmeans_boxes3 = KMeans(n_clusters = 12, init = 'k-means++', random_state = 42)
# 对数据进行聚类,并返回每个样本所属的簇的索引
y_kmeans_boxes3 = kmeans_boxes3.fit_predict(df_boxes3_kmeans)
# 在df_blob_kmeans数据集中创建名为“Cluster”的列,并将y_kmeans_blob赋值给该列
df_blob_kmeans['Cluster'] = y_kmeans_blob
# 在df_dart_kmeans数据集中创建名为“Cluster”的列,并将y_kmeans_dart赋值给该列
df_dart_kmeans['Cluster'] = y_kmeans_dart
# 在df_basic_kmeans数据集中创建名为“Cluster”的列,并将y_kmeans_basic赋值给该列
df_basic_kmeans['Cluster'] = y_kmeans_basic
# 在df_outliers_kmeans数据集中创建名为“Cluster”的列,并将y_kmeans_outliers赋值给该列
df_outliers_kmeans['Cluster'] = y_kmeans_outliers
# 在df_spiral2_kmeans数据集中创建名为“Cluster”的列,并将y_kmeans_spiral2赋值给该列
df_spiral2_kmeans['Cluster'] = y_kmeans_spiral2
# 在df_boxes3_kmeans数据集中创建名为“Cluster”的列,并将y_kmeans_boxes3赋值给该列
df_boxes3_kmeans['Cluster'] = y_kmeans_boxes3
4.4 比较结果
# 创建子图
fig, axes = plt.subplots(nrows=6, ncols=2,figsize=(10,30))
# 创建一个包含6行2列的子图,总共12个子图,设置整个图的大小为10x30
# 设置总标题
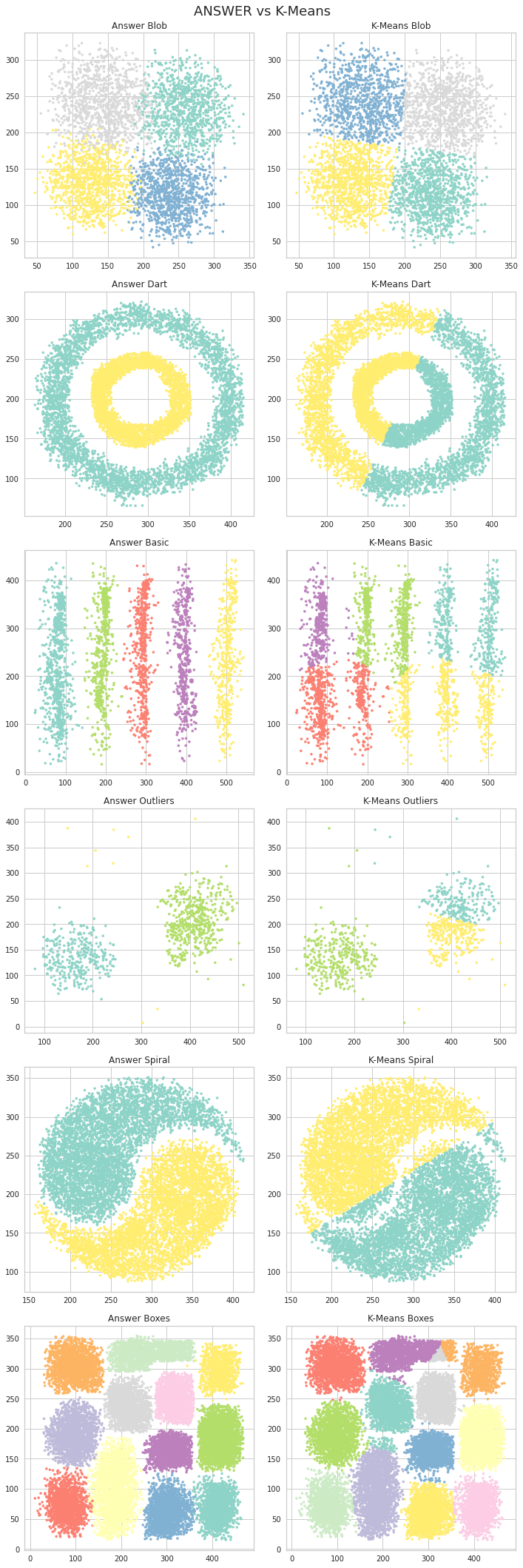
fig.suptitle('ANSWER vs K-Means\n', size = 18)
# 设置总标题为'ANSWER vs K-Means',字体大小为18
# 绘制Answer Blob子图
axes[0,0].scatter(blob_df['x'], blob_df['y'], c=blob_df['color'], s=10, cmap = "Set3")
# 在第1行第1列的子图中绘制散点图,横坐标为blob_df的'x'列,纵坐标为blob_df的'y'列,点的颜色根据blob_df的'color'列确定,点的大小为10,使用"Set3"颜色映射
axes[0,0].set_title("Answer Blob")
# 设置第1行第1列子图的标题为"Answer Blob"
# 绘制K-Means Blob子图
axes[0,1].scatter(df_blob_kmeans['x'], df_blob_kmeans['y'], c=df_blob_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第1行第2列的子图中绘制散点图,横坐标为df_blob_kmeans的'x'列,纵坐标为df_blob_kmeans的'y'列,点的颜色根据df_blob_kmeans的'Cluster'列确定,点的大小为10,使用"Set3"颜色映射
axes[0,1].set_title("K-Means Blob")
# 设置第1行第2列子图的标题为"K-Means Blob"
# 绘制Answer Dart子图
axes[1,0].scatter(dart_df['x'], dart_df['y'], c=dart_df['color'], s=10, cmap = "Set3")
# 在第2行第1列的子图中绘制散点图,横坐标为dart_df的'x'列,纵坐标为dart_df的'y'列,点的颜色根据dart_df的'color'列确定,点的大小为10,使用"Set3"颜色映射
axes[1,0].set_title("Answer Dart")
# 设置第2行第1列子图的标题为"Answer Dart"
# 绘制K-Means Dart子图
axes[1,1].scatter(df_dart_kmeans['x'], df_dart_kmeans['y'], c=df_dart_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第2行第2列的子图中绘制散点图,横坐标为df_dart_kmeans的'x'列,纵坐标为df_dart_kmeans的'y'列,点的颜色根据df_dart_kmeans的'Cluster'列确定,点的大小为10,使用"Set3"颜色映射
axes[1,1].set_title("K-Means Dart")
# 设置第2行第2列子图的标题为"K-Means Dart"
# 绘制Answer Basic子图
axes[2,0].scatter(basic2_df['x'], basic2_df['y'], c=basic2_df['color'], s=10, cmap = "Set3")
# 在第3行第1列的子图中绘制散点图,横坐标为basic2_df的'x'列,纵坐标为basic2_df的'y'列,点的颜色根据basic2_df的'color'列确定,点的大小为10,使用"Set3"颜色映射
axes[2,0].set_title("Answer Basic")
# 设置第3行第1列子图的标题为"Answer Basic"
# 绘制K-Means Basic子图
axes[2,1].scatter(df_basic_kmeans['x'], df_basic_kmeans['y'], c=df_basic_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第3行第2列的子图中绘制散点图,横坐标为df_basic_kmeans的'x'列,纵坐标为df_basic_kmeans的'y'列,点的颜色根据df_basic_kmeans的'Cluster'列确定,点的大小为10,使用"Set3"颜色映射
axes[2,1].set_title("K-Means Basic")
# 设置第3行第2列子图的标题为"K-Means Basic"
# 绘制Answer Outliers子图
axes[3,0].scatter(outliers_df['x'], outliers_df['y'], c=outliers_df['color'], s=10, cmap = "Set3")
# 在第4行第1列的子图中绘制散点图,横坐标为outliers_df的'x'列,纵坐标为outliers_df的'y'列,点的颜色根据outliers_df的'color'列确定,点的大小为10,使用"Set3"颜色映射
axes[3,0].set_title("Answer Outliers")
# 设置第4行第1列子图的标题为"Answer Outliers"
# 绘制K-Means Outliers子图
axes[3,1].scatter(df_outliers_kmeans['x'], df_outliers_kmeans['y'], c=df_outliers_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第4行第2列的子图中绘制散点图,横坐标为df_outliers_kmeans的'x'列,纵坐标为df_outliers_kmeans的'y'列,点的颜色根据df_outliers_kmeans的'Cluster'列确定,点的大小为10,使用"Set3"颜色映射
axes[3,1].set_title("K-Means Outliers")
# 设置第4行第2列子图的标题为"K-Means Outliers"
# 绘制Answer Spiral子图
axes[4,0].scatter(spiral2_df['x'], spiral2_df['y'], c=spiral2_df['color'], s=10, cmap = "Set3")
# 在第5行第1列的子图中绘制散点图,横坐标为spiral2_df的'x'列,纵坐标为spiral2_df的'y'列,点的颜色根据spiral2_df的'color'列确定,点的大小为10,使用"Set3"颜色映射
axes[4,0].set_title("Answer Spiral")
# 设置第5行第1列子图的标题为"Answer Spiral"
# 绘制K-Means Spiral子图
axes[4,1].scatter(df_spiral2_kmeans['x'], df_spiral2_kmeans['y'], c=df_spiral2_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第5行第2列的子图中绘制散点图,横坐标为df_spiral2_kmeans的'x'列,纵坐标为df_spiral2_kmeans的'y'列,点的颜色根据df_spiral2_kmeans的'Cluster'列确定,点的大小为10,使用"Set3"颜色映射
axes[4,1].set_title("K-Means Spiral")
# 设置第5行第2列子图的标题为"K-Means Spiral"
# 绘制Answer Boxes子图
axes[5,0].scatter(boxes3_df['x'], boxes3_df['y'], c=boxes3_df['color'], s=10, cmap = "Set3")
# 在第6行第1列的子图中绘制散点图,横坐标为boxes3_df的'x'列,纵坐标为boxes3_df的'y'列,点的颜色根据boxes3_df的'color'列确定,点的大小为10,使用"Set3"颜色映射
axes[5,0].set_title("Answer Boxes")
# 设置第6行第1列子图的标题为"Answer Boxes"
# 绘制K-Means Boxes子图
axes[5,1].scatter(df_boxes3_kmeans['x'], df_boxes3_kmeans['y'], c=df_boxes3_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第6行第2列的子图中绘制散点图,横坐标为df_boxes3_kmeans的'x'列,纵坐标为df_boxes3_kmeans的'y'列,点的颜色根据df_boxes3_kmeans的'Cluster'列确定,点的大小为10,使用"Set3"颜色映射
axes[5,1].set_title("K-Means Boxes")
# 设置第6行第2列子图的标题为"K-Means Boxes"
# 调整子图布局
plt.tight_layout()
# 调整子图的布局,使得子图之间的间距合适,防止重叠
4.5 在在线零售数据上使用K-Means算法
# 将df2复制给df_kmeans,因为我们需要引用之前的df来添加聚类编号
df_kmeans = df2.copy()
# 检查每个聚类中的项数,并创建一个名为'Cluster'的列
df_kmeans['Cluster'] = y_kmeans
# 统计每个聚类中的项数,并显示结果
df_kmeans['Cluster'].value_counts()
1 1945
4 853
0 441
5 308
2 215
3 142
Name: Cluster, dtype: int64
# 设置图形大小
plt.figure(figsize=(15,7))
# 绘制散点图
sns.scatterplot(data=df_kmeans, x='Amount', y='Frequency', hue='Cluster', s=15, palette="Set3")
# 参数解释:
# data:要绘制的数据集
# x:x轴数据列名
# y:y轴数据列名
# hue:根据该列的值对数据点进行着色
# s:数据点的大小
# palette:颜色调色板,用于设置数据点的颜色
<AxesSubplot:xlabel='Amount', ylabel='Frequency'>

5. 层次聚类
层次聚类(也称为层次聚类分析或HCA)是一种聚类分析方法,旨在构建一个聚类的层次结构。它根据对象之间的相似性将对象分组到聚类中。一般来说,合并和分割是以贪婪的方式确定的。层次聚类的结果通常以树状图的形式呈现。
在你有一些特别感兴趣的观察结果,并且想要能够识别与这些观察结果相似的观察结果的情况下,层次聚类特别有用。
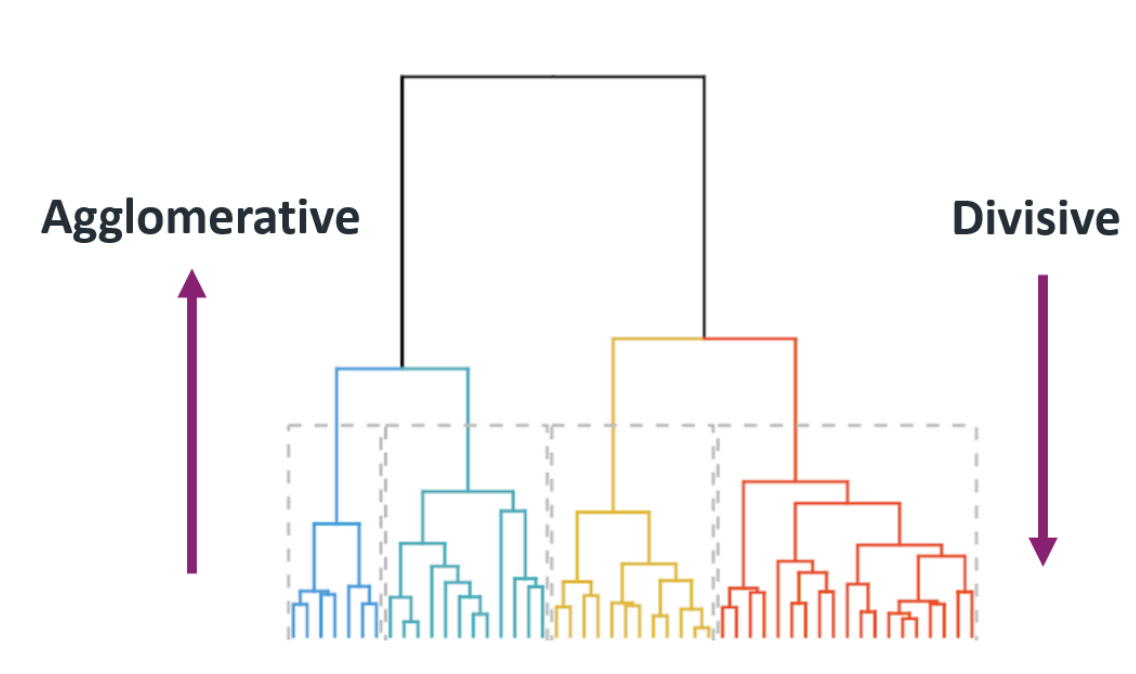
层次聚类可以是:
凝聚型 - 它从一个单独的元素开始,然后将它们分组成单一的聚类。
分裂型 - 它从一个完整的数据集开始,将其分割成分区。
凝聚型聚类最擅长找到小的聚类。当算法完成时,最终结果看起来像一个树状图,这样你就可以轻松地可视化聚类。
5.1 层次聚类的优缺点
层次聚类的优点:
-
获取与给定观测值最相似的观测值 - 该算法提供了关于哪些观测值彼此最相似的详细信息。许多其他算法都不提供这种详细信息。
-
对初始化条件不太敏感 - 它对于设置的种子或数据集的顺序等初始化条件不敏感。如果您使用不同的初始化条件重新运行分析,通常会得到非常相似的结果,有时甚至是完全相同的结果。
-
可以适应包含分类变量的情况 - 它可以适应相对容易包含数值和分类变量混合的情况。为了做到这一点,您必须确保使用的距离度量适用于混合数据类型,例如Grower’s距离。
-
对异常值不太敏感 - 少数异常值的存在不太可能影响算法对其他数据点的执行方式。
-
对聚类形状的假设要求较低 - 算法对聚类的形状没有那么严格的假设要求。根据您使用的距离度量,某些聚类形状可能比其他形状更容易被检测到,但具有更大的灵活性。
层次聚类的缺点:
-
相对较慢 - 这是一个数学上非常复杂的算法。层次聚类通常需要计算数据集中所有观测值之间的成对距离,因此随着数据集大小的增加,所需的计算量会迅速增长。
-
必须指定聚类的数量 - 但在算法的主要部分运行后,可以更改聚类的数量,因此我们可以尝试使用不同数量的聚类而无需从头运行算法。
-
对比例敏感 - 在运行聚类之前,我们可能需要对数据进行重新缩放。敏感性的确切程度将取决于我们用于计算点之间距离的距离度量。
-
受启发式方法的影响较大 - 这导致在过程中需要大量手动干预,因此需要应用/领域特定的知识来分析结果是否有意义。
-
可能难以可视化 - 如果数据样本的数量增加,那么通过可视化树状图进行分析和决策将变得不可能。
5.2 层次聚类的变体
BIRCH 是一种层次聚类的扩展,可以更快地处理大型数据集。与标准的层次聚类相比,它具有更低的内存需求。
5.3 在数据集上训练层次聚类模型
# 复制数据集df3并命名为df_AgglomerativeC
df_AgglomerativeC = df3.copy()
# 复制数据集blob_df并命名为df_blob_AgglomerativeC
df_blob_AgglomerativeC = blob_df.copy()
# 复制数据集dart_df并命名为df_dart_AgglomerativeC
df_dart_AgglomerativeC = dart_df.copy()
# 复制数据集basic2_df并命名为df_basic2_AgglomerativeC
df_basic2_AgglomerativeC = basic2_df.copy()
# 复制数据集outliers_df并命名为df_outliers_AgglomerativeC
df_outliers_AgglomerativeC = outliers_df.copy()
# 复制数据集spiral2_df并命名为df_spiral2_AgglomerativeC
df_spiral2_AgglomerativeC = spiral2_df.copy()
# 复制数据集boxes3_df并命名为df_boxes3_AgglomerativeC
df_boxes3_AgglomerativeC = boxes3_df.copy()
# 以下代码是对数据框中的某一列进行删除操作
# df_blob_AgglomerativeC是一个数据框,通过调用drop()函数,删除了名为'color'的列
# inplace=True表示在原数据框上进行修改,而不是返回一个新的数据框
# 删除df_blob_AgglomerativeC数据框中的'color'列
df_blob_AgglomerativeC.drop(['color'], axis=1, inplace=True)
# 删除df_dart_AgglomerativeC数据框中的'color'列
df_dart_AgglomerativeC.drop(['color'], axis=1, inplace=True)
# 删除df_basic2_AgglomerativeC数据框中的'color'列
df_basic2_AgglomerativeC.drop(['color'], axis=1, inplace=True)
# 删除df_outliers_AgglomerativeC数据框中的'color'列
df_outliers_AgglomerativeC.drop(['color'], axis=1, inplace=True)
# 删除df_spiral2_AgglomerativeC数据框中的'color'列
df_spiral2_AgglomerativeC.drop(['color'], axis=1, inplace=True)
# 删除df_boxes3_AgglomerativeC数据框中的'color'列
df_boxes3_AgglomerativeC.drop(['color'], axis=1, inplace=True)
# 导入AgglomerativeClustering模块
from sklearn.cluster import AgglomerativeClustering
# 创建AgglomerativeClustering对象,设置聚类数为6,相似度度量为欧氏距离,链接方式为ward
AgglomerativeC = AgglomerativeClustering(n_clusters=6, affinity='euclidean', linkage='ward')
# 使用AgglomerativeC对象对数据集df_AgglomerativeC进行聚类,并返回聚类结果
y_AgglomerativeC = AgglomerativeC.fit_predict(df_AgglomerativeC)
# 创建AgglomerativeClustering对象,设置聚类数为4,相似度度量为欧氏距离,链接方式为ward
AgglomerativeC_blob = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')
# 使用AgglomerativeC_blob对象对数据集df_blob_AgglomerativeC进行聚类,并返回聚类结果
y_AgglomerativeC_blob = AgglomerativeC_blob.fit_predict(df_blob_AgglomerativeC)
# 创建AgglomerativeClustering对象,设置聚类数为2,相似度度量为欧氏距离,链接方式为ward
AgglomerativeC_dart = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
# 使用AgglomerativeC_dart对象对数据集df_dart_AgglomerativeC进行聚类,并返回聚类结果
y_AgglomerativeC_dart = AgglomerativeC_dart.fit_predict(df_dart_AgglomerativeC)
# 创建AgglomerativeClustering对象,设置聚类数为5,相似度度量为欧氏距离,链接方式为ward
AgglomerativeC_basic = AgglomerativeClustering(n_clusters=5, affinity='euclidean', linkage='ward')
# 使用AgglomerativeC_basic对象对数据集df_basic2_AgglomerativeC进行聚类,并返回聚类结果
y_AgglomerativeC_basic = AgglomerativeC_basic.fit_predict(df_basic2_AgglomerativeC)
# 创建AgglomerativeClustering对象,设置聚类数为3,相似度度量为欧氏距离,链接方式为ward
AgglomerativeC_outliers = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='ward')
# 使用AgglomerativeC_outliers对象对数据集df_outliers_AgglomerativeC进行聚类,并返回聚类结果
y_AgglomerativeC_outliers = AgglomerativeC_outliers.fit_predict(df_outliers_AgglomerativeC)
# 创建AgglomerativeClustering对象,设置聚类数为2,相似度度量为欧氏距离,链接方式为ward
AgglomerativeC_spiral2 = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
# 使用AgglomerativeC_spiral2对象对数据集df_spiral2_AgglomerativeC进行聚类,并返回聚类结果
y_AgglomerativeC_spiral2 = AgglomerativeC_spiral2.fit_predict(df_spiral2_AgglomerativeC)
# 创建AgglomerativeClustering对象,设置聚类数为12,相似度度量为欧氏距离,链接方式为ward
AgglomerativeC_boxes3 = AgglomerativeClustering(n_clusters=12, affinity='euclidean', linkage='ward')
# 使用AgglomerativeC_boxes3对象对数据集df_boxes3_AgglomerativeC进行聚类,并返回聚类结果
y_AgglomerativeC_boxes3 = AgglomerativeC_boxes3.fit_predict(df_boxes3_AgglomerativeC)
# 在数据集df_blob_AgglomerativeC中创建'Cluster'列,并将聚类结果y_AgglomerativeC_blob赋值给该列
df_blob_AgglomerativeC['Cluster'] = y_AgglomerativeC_blob
# 在数据集df_dart_AgglomerativeC中创建'Cluster'列,并将聚类结果y_AgglomerativeC_dart赋值给该列
df_dart_AgglomerativeC['Cluster'] = y_AgglomerativeC_dart
# 在数据集df_basic2_AgglomerativeC中创建'Cluster'列,并将聚类结果y_AgglomerativeC_basic赋值给该列
df_basic2_AgglomerativeC['Cluster'] = y_AgglomerativeC_basic
# 在数据集df_outliers_AgglomerativeC中创建'Cluster'列,并将聚类结果y_AgglomerativeC_outliers赋值给该列
df_outliers_AgglomerativeC['Cluster'] = y_AgglomerativeC_outliers
# 在数据集df_spiral2_AgglomerativeC中创建'Cluster'列,并将聚类结果y_AgglomerativeC_spiral2赋值给该列
df_spiral2_AgglomerativeC['Cluster'] = y_AgglomerativeC_spiral2
# 在数据集df_boxes3_AgglomerativeC中创建'Cluster'列,并将聚类结果y_AgglomerativeC_boxes3赋值给该列
df_boxes3_AgglomerativeC['Cluster'] = y_AgglomerativeC_boxes3
5.4 比较结果
# 创建子图fig, axes = plt.subplots(nrows=6, ncols=2,figsize=(10,30))
# 创建一个6行2列的子图,总共有12个子图,设置子图的大小为10x30
# 设置总标题fig.suptitle('ANSWER vs Hierarchical clustering\n', size = 18)
# 设置总标题为'ANSWER vs Hierarchical clustering\n',字体大小为18
# 绘制Answer Blob散点图
axes[0,0].scatter(blob_df['x'], blob_df['y'], c=blob_df['color'], s=10, cmap = "Set3")
# 在第1行第1列的子图中绘制Answer Blob散点图
# x轴数据为blob_df的'x'列,y轴数据为blob_df的'y'列,颜色根据blob_df的'color'列确定,点的大小为10,颜色映射为"Set3"
axes[0,0].set_title("Answer Blob")
# 设置第1行第1列子图的标题为"Answer Blob"
# 绘制Hierarchical clustering Blob散点图
axes[0,1].scatter(df_blob_AgglomerativeC['x'], df_blob_AgglomerativeC['y'], c=df_blob_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第1行第2列的子图中绘制Hierarchical clustering Blob散点图
# x轴数据为df_blob_AgglomerativeC的'x'列,y轴数据为df_blob_AgglomerativeC的'y'列,颜色根据df_blob_AgglomerativeC的'Cluster'列确定,点的大小为10,颜色映射为"Set3"
axes[0,1].set_title("Hierarchical clustering Blob")
# 设置第1行第2列子图的标题为"Hierarchical clustering Blob"
# 绘制Answer Dart散点图
axes[1,0].scatter(dart_df['x'], dart_df['y'], c=dart_df['color'], s=10, cmap = "Set3")
# 在第2行第1列的子图中绘制Answer Dart散点图
# x轴数据为dart_df的'x'列,y轴数据为dart_df的'y'列,颜色根据dart_df的'color'列确定,点的大小为10,颜色映射为"Set3"
axes[1,0].set_title("Answer Dart")
# 设置第2行第1列子图的标题为"Answer Dart"
# 绘制Hierarchical clustering Dart散点图
axes[1,1].scatter(df_dart_AgglomerativeC['x'], df_dart_AgglomerativeC['y'], c=df_dart_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第2行第2列的子图中绘制Hierarchical clustering Dart散点图
# x轴数据为df_dart_AgglomerativeC的'x'列,y轴数据为df_dart_AgglomerativeC的'y'列,颜色根据df_dart_AgglomerativeC的'Cluster'列确定,点的大小为10,颜色映射为"Set3"
axes[1,1].set_title("Hierarchical clustering Dart")
# 设置第2行第2列子图的标题为"Hierarchical clustering Dart"
# 绘制Answer Basic散点图
axes[2,0].scatter(basic2_df['x'], basic2_df['y'], c=basic2_df['color'], s=10, cmap = "Set3")
# 在第3行第1列的子图中绘制Answer Basic散点图
# x轴数据为basic2_df的'x'列,y轴数据为basic2_df的'y'列,颜色根据basic2_df的'color'列确定,点的大小为10,颜色映射为"Set3"
axes[2,0].set_title("Answer Basic")
# 设置第3行第1列子图的标题为"Answer Basic"
# 绘制Hierarchical clustering Basic散点图
axes[2,1].scatter(df_basic2_AgglomerativeC['x'], df_basic2_AgglomerativeC['y'], c=df_basic2_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第3行第2列的子图中绘制Hierarchical clustering Basic散点图
# x轴数据为df_basic2_AgglomerativeC的'x'列,y轴数据为df_basic2_AgglomerativeC的'y'列,颜色根据df_basic2_AgglomerativeC的'Cluster'列确定,点的大小为10,颜色映射为"Set3"
axes[2,1].set_title("Hierarchical clustering Basic")
# 设置第3行第2列子图的标题为"Hierarchical clustering Basic"
# 绘制Answer Outliers散点图
axes[3,0].scatter(outliers_df['x'], outliers_df['y'], c=outliers_df['color'], s=10, cmap = "Set3")
# 在第4行第1列的子图中绘制Answer Outliers散点图
# x轴数据为outliers_df的'x'列,y轴数据为outliers_df的'y'列,颜色根据outliers_df的'color'列确定,点的大小为10,颜色映射为"Set3"
axes[3,0].set_title("Answer Outliers")
# 设置第4行第1列子图的标题为"Answer Outliers"
# 绘制Hierarchical clustering Outliers散点图
axes[3,1].scatter(df_outliers_AgglomerativeC['x'], df_outliers_AgglomerativeC['y'], c=df_outliers_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第4行第2列的子图中绘制Hierarchical clustering Outliers散点图
# x轴数据为df_outliers_AgglomerativeC的'x'列,y轴数据为df_outliers_AgglomerativeC的'y'列,颜色根据df_outliers_AgglomerativeC的'Cluster'列确定,点的大小为10,颜色映射为"Set3"
axes[3,1].set_title("Hierarchical clustering Outliers")
# 设置第4行第2列子图的标题为"Hierarchical clustering Outliers"
# 绘制Answer Spiral散点图
axes[4,0].scatter(spiral2_df['x'], spiral2_df['y'], c=spiral2_df['color'], s=10, cmap = "Set3")
# 在第5行第1列的子图中绘制Answer Spiral散点图
# x轴数据为spiral2_df的'x'列,y轴数据为spiral2_df的'y'列,颜色根据spiral2_df的'color'列确定,点的大小为10,颜色映射为"Set3"
axes[4,0].set_title("Answer Spiral")
# 设置第5行第1列子图的标题为"Answer Spiral"
# 绘制Hierarchical clustering Spiral散点图
axes[4,1].scatter(df_spiral2_AgglomerativeC['x'], df_spiral2_AgglomerativeC['y'], c=df_spiral2_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第5行第2列的子图中绘制Hierarchical clustering Spiral散点图
# x轴数据为df_spiral2_AgglomerativeC的'x'列,y轴数据为df_spiral2_AgglomerativeC的'y'列,颜色根据df_spiral2_AgglomerativeC的'Cluster'列确定,点的大小为10,颜色映射为"Set3"
axes[4,1].set_title("Hierarchical clustering Spiral")
# 设置第5行第2列子图的标题为"Hierarchical clustering Spiral"
# 绘制Answer Boxes散点图
axes[5,0].scatter(boxes3_df['x'], boxes3_df['y'], c=boxes3_df['color'], s=10, cmap = "Set3")
# 在第6行第1列的子图中绘制Answer Boxes散点图
# x轴数据为boxes3_df的'x'列,y轴数据为boxes3_df的'y'列,颜色根据boxes3_df的'color'列确定,点的大小为10,颜色映射为"Set3"
axes[5,0].set_title("Answer Boxes")
# 设置第6行第1列子图的标题为"Answer Boxes"
# 绘制Hierarchical clustering Boxes散点图
axes[5,1].scatter(df_boxes3_AgglomerativeC['x'], df_boxes3_AgglomerativeC['y'], c=df_boxes3_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第6行第2列的子图中绘制Hierarchical clustering Boxes散点图
# x轴数据为df_boxes3_AgglomerativeC的'x'列,y轴数据为df_boxes3_AgglomerativeC的'y'列,颜色根据df_boxes3_AgglomerativeC的'Cluster'列确定,点的大小为10,颜色映射为"Set3"
axes[5,1].set_title("Hierarchical clustering Boxes")
# 设置第6行第2列子图的标题为"Hierarchical clustering Boxes"
# 调整子图布局
plt.tight_layout()
# 调整子图的布局,使得子图之间的间距合适,避免重叠

5.5 在线零售数据的层次聚类
# 将df2复制给df_AgglomerativeC,因为我们需要引用之前的df来添加聚类号码
df_AgglomerativeC = df2.copy()
# 检查每个聚类中的项数,并创建一个名为'Cluster'的列
df_AgglomerativeC['Cluster'] = y_AgglomerativeC
# 统计每个聚类中的项数
df_AgglomerativeC['Cluster'].value_counts()
2 1848
4 992
1 398
0 334
5 193
3 139
Name: Cluster, dtype: int64
# 设置图形大小
plt.figure(figsize=(15,7))
# 绘制散点图
sns.scatterplot(data=df_AgglomerativeC, x='Amount', y='Frequency', hue='Cluster', s=15, palette="Set3")
# 添加文注释:设置图形的大小为15x7
# 添加文注释:使用seaborn库的scatterplot函数绘制散点图
# 添加文注释:散点图的x轴数据为'Amount',y轴数据为'Frequency'
# 添加文注释:根据'Cluster'列的值对散点进行着色
# 添加文注释:散点的大小为15,颜色使用"Set3"调色板
<AxesSubplot:xlabel='Amount', ylabel='Frequency'>

6. DBSCAN聚类算法
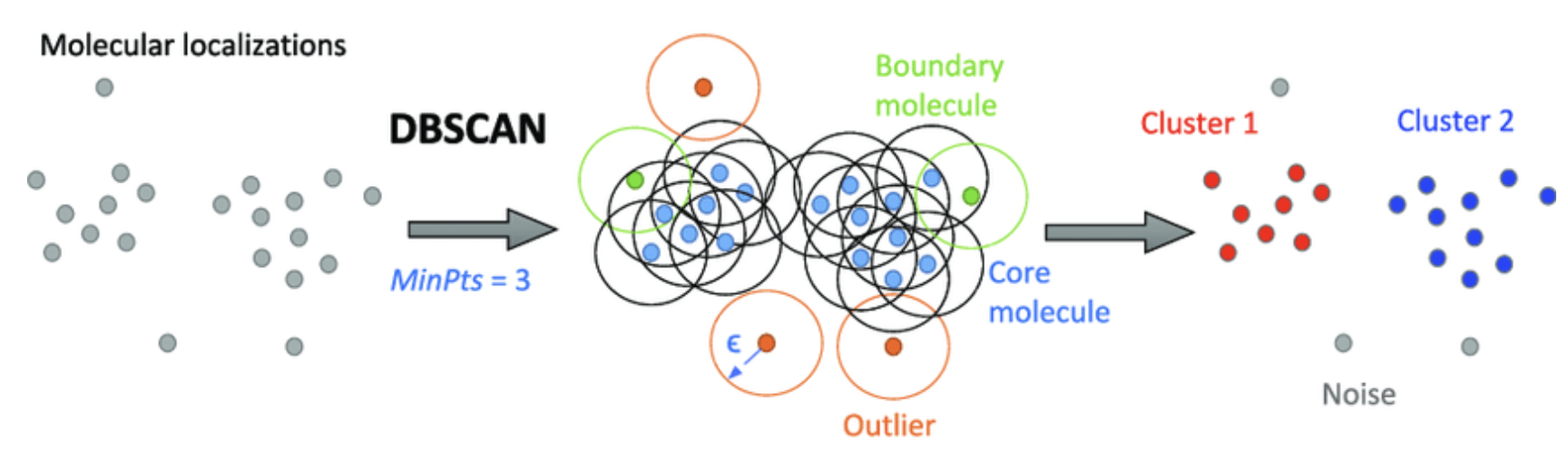
DBSCAN代表密度聚类应用程序与噪声。它是一种基于密度的聚类算法。
它能够找到不规则形状的聚类。它通过低密度区域分离区域,因此也能很好地检测异常值。当处理奇异形状的数据时,该算法比k-means更好。
DBSCAN
DBSCAN是一种密度聚类算法,它可以将数据点分为不同的簇。它的核心思想是将密度高的点聚集在一起,而将密度低的点与其他点分开。
6.1 DBSCAN的优缺点
DBSCAN的优点:
- 处理不规则形状和大小的簇 - DBSCAN是少数几个对簇形状做出最少假设的算法之一。这意味着DBSCAN可以用于检测奇怪或不规则形状的簇。
- 鲁棒性强 - 该算法能够检测异常值并将其完全排除在簇之外。
- 不需要指定簇的数量 - DBSCAN的另一个优点是它不需要用户指定簇的数量。DBSCAN可以自动检测数据中存在的簇的数量。这对于您不知道应该有多少簇的情况非常有用。
- 对初始化条件不太敏感 - DBSCAN对初始化条件的敏感性较低,如数据集中观测值的顺序和使用的种子,比某些其他聚类算法要低。
- 相对较快 - DBSCAN通常比K-Means聚类慢,但比分层聚类和谱聚类快。
DBSCAN的缺点:
- 难以纳入分类特征 - 在大多数特征为数值型的情况下,应使用DBSCAN。
- 需要数据密度下降才能检测簇边界 - 在簇之间的数据点密度必须下降,以便算法能够检测簇之间的边界。如果有多个簇重叠而没有数据密度下降,则它们可能被分组为单个簇。
- 难以处理密度变化的簇 - DBSCAN通过查看数据点密度低于某个阈值的地方来确定簇的起始和结束位置。在不太密集的簇中找到捕获所有点的阈值可能很困难,而在更密集的簇中排除太多的杂散异常值也可能很困难。
- 对比例敏感 - DBSCAN对变量的比例敏感。这意味着,如果变量的比例差异很大,我们需要重新缩放变量。
- 难以处理高维数据 - DBSCAN的性能在存在许多特征的情况下往往会降低。如果我们有高维数据集,应使用降维或特征选择技术来减少特征数量。
- 需要设置Epsilon和MinPts参数。这可能有些棘手。
6.2 选择正确的初始参数
DBSCAN算法需要两个参数 - 选择正确的数值对于该算法至关重要:
- Epsilon (ε) 是要围绕每个数据点创建的圆的半径,用于检查密度。
该技术计算每个点与其k个最近邻点之间的平均距离,其中k = 您选择的MinPts值。然后,将平均k距离按升序绘制在k距离图上。可以从K距离图中决定epsilon的值。该图中最大曲率点(拐点)告诉我们epsilon的值(即图形具有最大斜率的位置)。
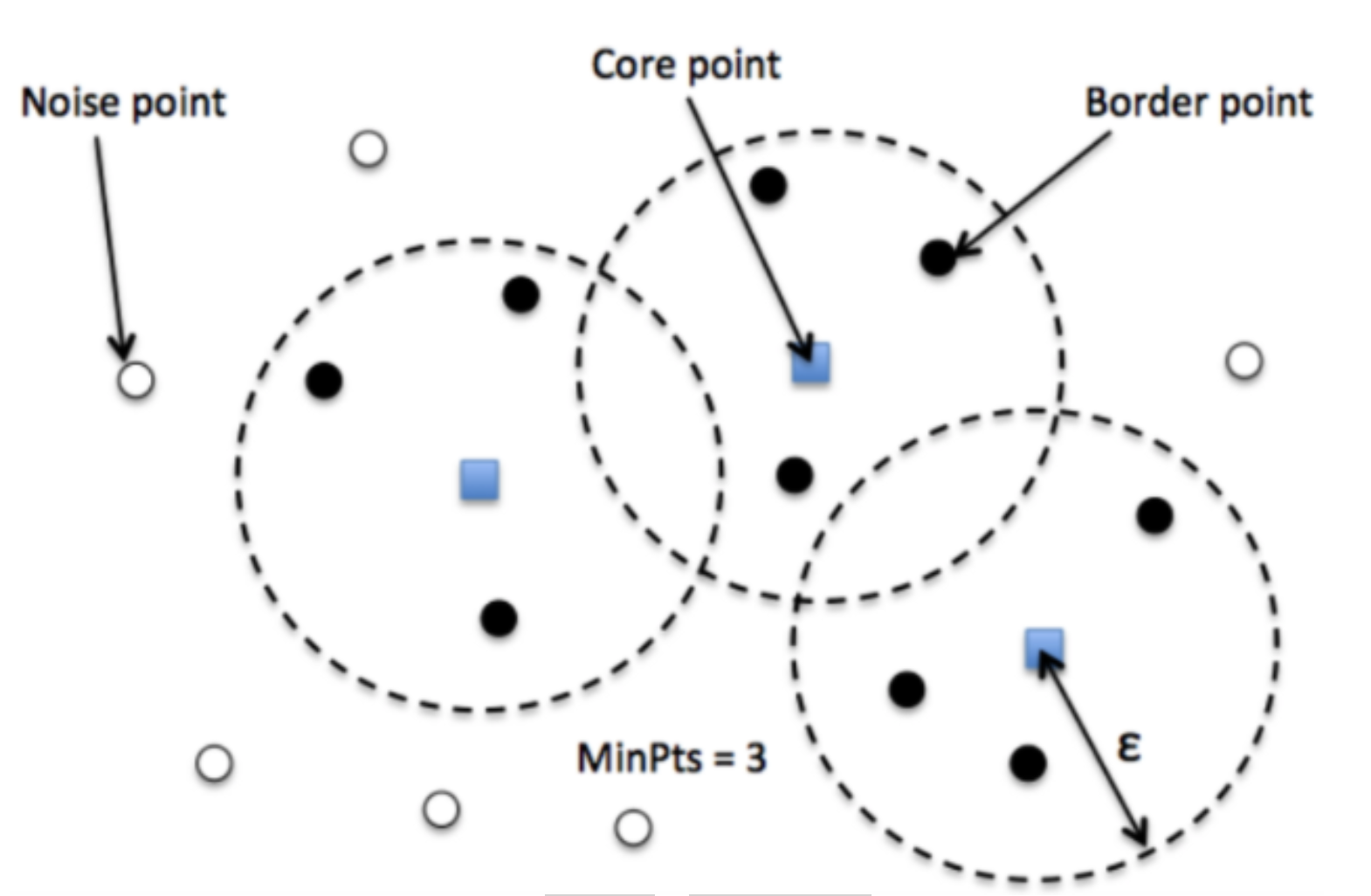
- minPoints (MinPts) 是在该圆内所需的最小数据点数,以便将该数据点分类为核心点。
没有自动确定DBSCAN的MinPts值的方法。将minPoints设置为1是没有意义的,因为这将导致每个点成为一个单独的簇。因此,它必须至少为3。通常,它是维度的两倍或维度+1。领域知识也决定了其值。
- 如果数据集噪声较大,请选择较大的MinPts值。
- 对于二维数据,请使用DBSCAN的默认值MinPts = 4(Ester等人,1996)。
minPoints的值应至少比数据集的维度大1:
- MinPts >= Dimensions * 2
或者
- MinPts >= Dimensions + 1
重要提示:
有时很难找到数据集的合适的Epsilon和MinPts参数。以下是一些提示:
-
对于大型和嘈杂的数据集,请使用较大的MinPts值。
-
如果得到的簇太大:减小epsilon。
-
如果得到的噪声太多:增加epsilon。
-
良好的聚类需要迭代。
为了绘制K距离图,我们需要计算数据集中每个数据点与其最近邻数据点之间的距离。我们可以使用sklearn.neighbors中的NearestNeighbors来实现这一点。
# 复制数据集df3并赋值给df_DBScan
df_DBScan = df3.copy()
# 复制数据集blob_df并赋值给df_blob_DBScan
df_blob_DBScan = blob_df.copy()
# 复制数据集dart_df并赋值给df_dart_DBScan
df_dart_DBScan = dart_df.copy()
# 复制数据集basic2_df并赋值给df_basic2_DBScan
df_basic2_DBScan = basic2_df.copy()
# 复制数据集outliers_df并赋值给df_outliers_DBScan
df_outliers_DBScan = outliers_df.copy()
# 复制数据集spiral2_df并赋值给df_spiral2_DBScan
df_spiral2_DBScan = spiral2_df.copy()
# 复制数据集boxes3_df并赋值给df_boxes3_DBScan
df_boxes3_DBScan = boxes3_df.copy()
# 导入NearestNeighbors类
from sklearn.neighbors import NearestNeighbors
# 创建一个NearestNeighbors对象,设置n_neighbors参数为4
nn = NearestNeighbors(n_neighbors=4)
# 使用df_dart_DBScan数据拟合NearestNeighbors模型
nbrs = nn.fit(df_dart_DBScan)
# 使用拟合好的模型计算最近邻的距离和索引
distances, indices = nbrs.kneighbors(df_dart_DBScan)
# 对距离进行排序
distances = np.sort(distances, axis=0)
# 取第二列的距离值
distances = distances[:,1]
# 创建一个6x6的图像
plt.figure(figsize=(6,6))
# 绘制距离图
plt.plot(distances)
# 设置图像标题和坐标轴标签
plt.title('K-distance Graph for "Dart df"',fontsize=20)
plt.xlabel('Data Points sorted by distance',fontsize=14)
plt.ylabel('Epsilon',fontsize=14)
# 显示图像
plt.show()

- 在K-Distance图中,epsilon的最佳值位于最大曲率点,本例中为8。
- 对于MinPts,我将选择4(2 * 维度)。
6.3 DBSCAN的变种算法
广义DBSCAN(GDBSCAN) - 将原始算法中的ε和minPts参数移动到谓词中,并将其删除。
OPTICS(Ordering Points To Identify the Clustering Structure) - 找到高密度的核心样本,并从它们扩展聚类。与DBSCAN不同,保持可变邻域半径的聚类层次结构。比当前sklearn实现的DBSCAN更适用于大型数据集。
HDBSCAN - DBSCAN的分层版本,也比OPTICS更快,可以从层次结构中提取由最突出的聚类组成的平坦分区。
DBSCAN也被用作子空间聚类算法PreDeCon和SUBCLU的一部分。
6.4 在数据集上训练DBSCAN聚类模型
在本节中,我们将使用DBSCAN算法在数据集上进行聚类。DBSCAN是一种密度聚类算法,它可以将数据点分为核心点、边界点和噪声点。该算法的优点是可以自动确定聚类数量,并且可以处理任意形状的聚类。在本节中,我们将使用sklearn库中的DBSCAN类来训练模型。
# 删除df_blob_DBScan中的'color'列
df_blob_DBScan.drop(['color'], axis=1, inplace=True)
# 删除df_dart_DBScan中的'color'列
df_dart_DBScan.drop(['color'], axis=1, inplace=True)
# 删除df_basic2_DBScan中的'color'列
df_basic2_DBScan.drop(['color'], axis=1, inplace=True)
# 删除df_outliers_DBScan中的'color'列
df_outliers_DBScan.drop(['color'], axis=1, inplace=True)
# 删除df_spiral2_DBScan中的'color'列
df_spiral2_DBScan.drop(['color'], axis=1, inplace=True)
# 删除df_boxes3_DBScan中的'color'列
df_boxes3_DBScan.drop(['color'], axis=1, inplace=True)
# 导入DBSCAN模型
from sklearn.cluster import DBSCAN
# 创建DBSCAN对象,设置eps为20,min_samples为9,使用欧氏距离作为距离度量
dbscan = DBSCAN(eps=20, min_samples=9, metric='euclidean')
# 使用DBSCAN模型对df_DBScan进行拟合和预测
y_DBScan = dbscan.fit_predict(df_DBScan)
# 创建不同参数的DBSCAN对象
DBScan_blob = DBSCAN(eps=13, min_samples=45, metric='euclidean')
DBScan_dart = DBSCAN(eps=8, min_samples=4, metric='euclidean')
DBScan_basic = DBSCAN(eps=15, min_samples=4, metric='euclidean')
DBScan_outliers = DBSCAN(eps=20, min_samples=4, metric='euclidean')
DBScan_spiral2 = DBSCAN(eps=5.7, min_samples=4, metric='euclidean')
DBScan_boxes3 = DBSCAN(eps=6, min_samples=4, metric='euclidean')
# 使用不同参数的DBSCAN模型对相应的数据集进行拟合和预测
y_DBScan_blob = DBScan_blob.fit_predict(df_blob_DBScan)
y_DBScan_dart = DBScan_dart.fit_predict(df_dart_DBScan)
y_DBScan_basic = DBScan_basic.fit_predict(df_basic2_DBScan)
y_DBScan_outliers = DBScan_outliers.fit_predict(df_outliers_DBScan)
y_DBScan_spiral2 = DBScan_spiral2.fit_predict(df_spiral2_DBScan)
y_DBScan_boxes3 = DBScan_boxes3.fit_predict(df_boxes3_DBScan)
# 在数据集中创建'Cluster'列
df_blob_DBScan['Cluster'] = y_DBScan_blob # 将DBScan算法聚类结果y_DBScan_blob赋值给df_blob_DBScan的'Cluster'列
df_dart_DBScan['Cluster'] = y_DBScan_dart # 将DBScan算法聚类结果y_DBScan_dart赋值给df_dart_DBScan的'Cluster'列
df_basic2_DBScan['Cluster'] = y_DBScan_basic # 将DBScan算法聚类结果y_DBScan_basic赋值给df_basic2_DBScan的'Cluster'列
df_outliers_DBScan['Cluster'] = y_DBScan_outliers # 将DBScan算法聚类结果y_DBScan_outliers赋值给df_outliers_DBScan的'Cluster'列
df_spiral2_DBScan['Cluster'] = y_DBScan_spiral2 # 将DBScan算法聚类结果y_DBScan_spiral2赋值给df_spiral2_DBScan的'Cluster'列
df_boxes3_DBScan['Cluster'] = y_DBScan_boxes3 # 将DBScan算法聚类结果y_DBScan_boxes3赋值给df_boxes3_DBScan的'Cluster'列
# 上述代码是将DBScan算法聚类结果赋值给数据集中的'Cluster'列,以便后续分析和可视化。每个数据集都有一个对应的聚类结果y_DBScan_xxx,将其赋值给对应的数据集的'Cluster'列即可。
6.5 比较结果
# 导入matplotlib库
import matplotlib.pyplot as plt
# 创建子图fig, axes,其中nrows=6表示创建6行,ncols=2表示创建2列,figsize=(10,30)表示设置子图的大小
fig, axes = plt.subplots(nrows=6, ncols=2, figsize=(10,30))
# 设置总标题fig.suptitle,size=18表示设置标题的字体大小
fig.suptitle('ANSWER vs DBSCAN clustering\n', size = 18)
# 绘制Answer Blob子图,其中c表示颜色,s表示点的大小,cmap表示颜色映射
axes[0,0].scatter(blob_df['x'], blob_df['y'], c=blob_df['color'], s=10, cmap = "Set3")
axes[0,0].set_title("Answer Blob") # 设置子图标题
# 绘制DBSCAN clustering Blob子图
axes[0,1].scatter(df_blob_DBScan['x'], df_blob_DBScan['y'], c=df_blob_DBScan['Cluster'], s=10, cmap = "Set3")
axes[0,1].set_title("DBSCAN clustering Blob") # 设置子图标题
# 绘制Answer Dart子图
axes[1,0].scatter(dart_df['x'], dart_df['y'], c=dart_df['color'], s=10, cmap = "Set3")
axes[1,0].set_title("Answer Dart") # 设置子图标题
# 绘制DBSCAN clustering Dart子图
axes[1,1].scatter(df_dart_DBScan['x'], df_dart_DBScan['y'], c=df_dart_DBScan['Cluster'], s=10, cmap = "Set3")
axes[1,1].set_title("DBSCAN clustering Dart") # 设置子图标题
# 绘制Answer Basic子图
axes[2,0].scatter(basic2_df['x'], basic2_df['y'], c=basic2_df['color'], s=10, cmap = "Set3")
axes[2,0].set_title("Answer Basic") # 设置子图标题
# 绘制DBSCAN clustering Basic子图
axes[2,1].scatter(df_basic2_DBScan['x'], df_basic2_DBScan['y'], c=df_basic2_DBScan['Cluster'], s=10, cmap = "Set3")
axes[2,1].set_title("DBSCAN clustering Basic") # 设置子图标题
# 绘制Answer Outliers子图
axes[3,0].scatter(outliers_df['x'], outliers_df['y'], c=outliers_df['color'], s=10, cmap = "Set3")
axes[3,0].set_title("Answer Outliers") # 设置子图标题
# 绘制DBSCAN clustering Outliers子图
axes[3,1].scatter(df_outliers_DBScan['x'], df_outliers_DBScan['y'], c=df_outliers_DBScan['Cluster'], s=10, cmap = "Set3")
axes[3,1].set_title("DBSCAN clustering Outliers") # 设置子图标题
# 绘制Answer Spiral子图
axes[4,0].scatter(spiral2_df['x'], spiral2_df['y'], c=spiral2_df['color'], s=10, cmap = "Set3")
axes[4,0].set_title("Answer Spiral") # 设置子图标题
# 绘制DBSCAN clustering Spiral子图
axes[4,1].scatter(df_spiral2_DBScan['x'], df_spiral2_DBScan['y'], c=df_spiral2_DBScan['Cluster'], s=10, cmap = "Set3")
axes[4,1].set_title("DBSCAN clustering Spiral") # 设置子图标题
# 绘制Answer Boxes子图
axes[5,0].scatter(boxes3_df['x'], boxes3_df['y'], c=boxes3_df['color'], s=10, cmap = "Set3")
axes[5,0].set_title("Answer Boxes") # 设置子图标题
# 绘制DBSCAN clustering Boxes子图
axes[5,1].scatter(df_boxes3_DBScan['x'], df_boxes3_DBScan['y'], c=df_boxes3_DBScan['Cluster'], s=10, cmap = "Set3")
axes[5,1].set_title("DBSCAN clustering Boxes") # 设置子图标题
# 调整子图布局
plt.tight_layout()

6.6 在在线零售数据上使用DBSCAN聚类模型
# 复制df2数据框并命名为df_DBScan,因为我们需要引用之前的df数据框来添加聚类编号
df_DBScan = df2.copy()
# 检查每个聚类中的数据项数量,并创建一个名为'Cluster'的列
df_DBScan['Cluster'] = y_DBScan
# 统计每个聚类的数量,并显示在'Cluster'列中
0 3904
Name: Cluster, dtype: int64
# 设置图形的大小
plt.figure(figsize=(15,7))
# 绘制散点图
sns.scatterplot(data=df_DBScan, x='Amount', y='Frequency', hue='Cluster', s=15, palette="Set3")
# 参数解释:
# - data:指定要绘制的数据集
# - x:指定x轴的数据列
# - y:指定y轴的数据列
# - hue:指定用于分组的数据列,根据该列的不同取值,散点图的颜色会有所区分
# - s:指定散点的大小
# - palette:指定颜色的调色板,用于设置散点的颜色
<AxesSubplot:xlabel='Amount', ylabel='Frequency'>

7. 高斯混合模型(GMM)
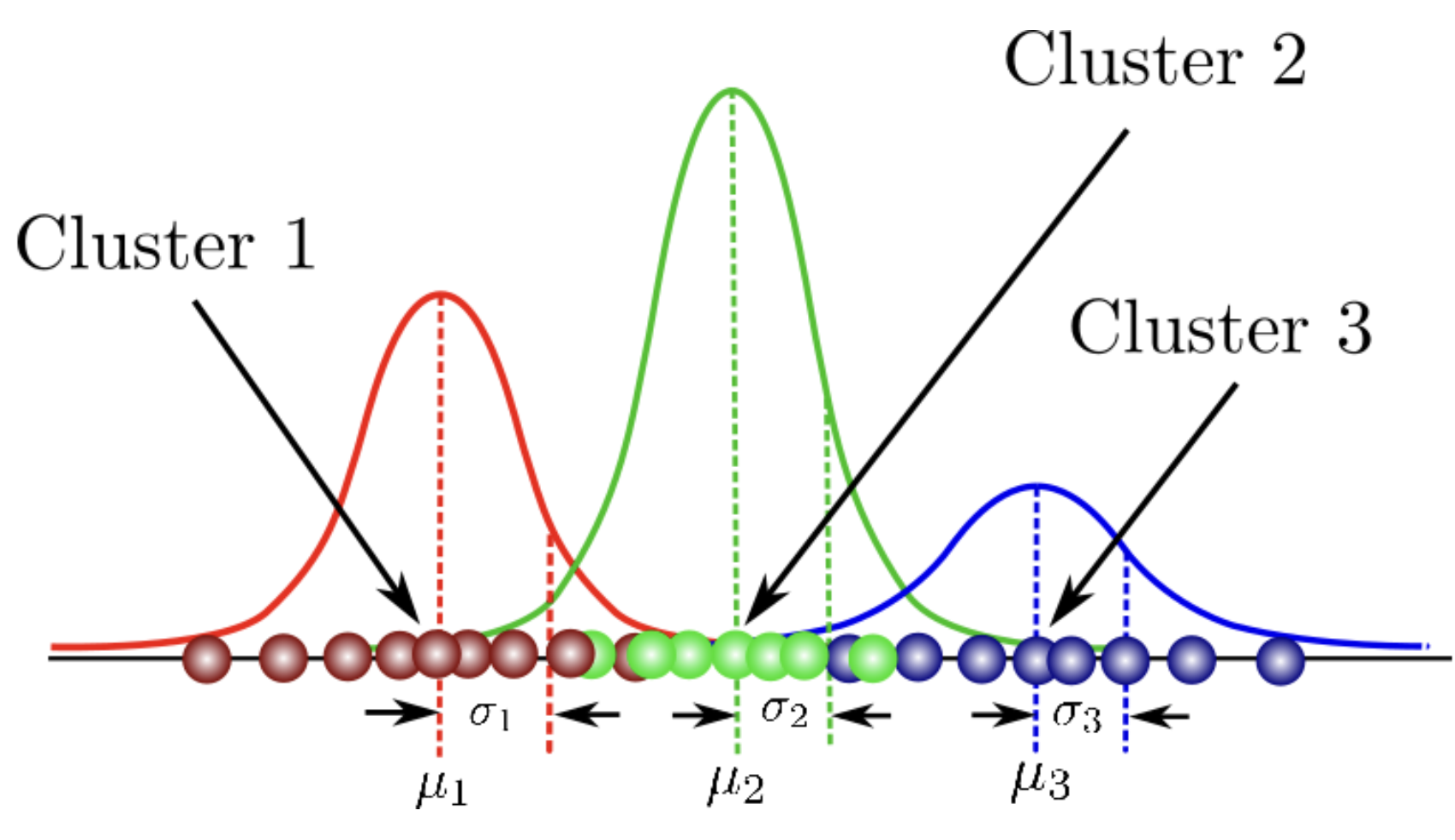
高斯混合模型(GMM)试图找到最能模拟任何输入数据集的多维高斯概率分布混合。在最简单的情况下,GMM可以像k-means一样用于查找聚类,但由于GMM在底层包含概率模型,因此还可以找到概率聚类分配。
高斯混合模型使用多个高斯分布来适应任意形状的数据。
在这个混合模型中,有几个单高斯模型作为隐藏层。因此,该模型计算数据点属于特定高斯分布的概率,这就是它所属的聚类。
7.1 高斯混合模型的优缺点
高斯混合模型(Gaussian Mixture Models)具有以下优点和缺点:
高斯混合模型(GMM)的优点:
- 对于属于每个簇的概率进行概率估计 - 模型提供了每个数据点属于每个簇的概率估计。当检查落在两个簇边界上的模糊数据点时,这些概率估计非常有用。
- 不假设球形簇 - 模型不假设所有簇都是均匀形状的球体。相反,高斯混合模型可以用来适应不同形状的簇。
- 处理不同大小的簇 - 高斯混合模型也可以用来适应不同大小的簇。
- 对尺度不敏感 - 这意味着在使用变量进行聚类之前,您可能不需要重新调整其尺度。
- 适应混合成员资格 - 在kmeans中,一个点属于一个且仅属于一个簇,而在GMM中,一个点属于每个簇的程度不同。这个程度是基于该点从每个簇的(多元)正态分布生成的概率,其中簇中心是分布的均值,簇协方差是其协方差。根据任务的不同,混合成员资格可能更合适(例如,新闻文章可以属于多个主题簇)或不合适(例如,生物可以属于只有一个物种)。
高斯混合模型(GMM)的缺点:
- 难以整合分类特征 - 模型在假设所有特征都服从正态分布的情况下运作,因此不容易适应分类数据。
- 假设特征服从正态分布 - 这意味着在使用此聚类算法之前,您应该花一些时间查看特征的分布情况。
- 对簇形状做出一些假设 - 这意味着在簇非常不规则形状的情况下,高斯混合模型的性能不会很好。
- 需要足够的数据来估计每个簇的协方差 - 您应该确保每个簇中有足够的数据点来充分估计协方差。所需的数据量并不是很大,但比不估计协方差矩阵的简单算法要大。
- 需要指定簇的数量 - 由于高斯混合模型在假设特征服从正态分布的情况下运作,它们可能会受到数据中存在许多异常值的情况的影响。一些高斯混合模型的实现允许将异常值分离到单独的簇中。
- 对初始化条件敏感 - 例如使用的种子和用于簇中心的起始点。这意味着如果多次运行算法,可能会得到不同的结果。
- 速度较慢 - 当数据集中有许多特征时,这一点尤其明显。
7.2 GMM的变体
Variational Bayesian Gaussian Mixture Model - avoids specifying the number of components in the Gaussian mixture model.
7.3 训练GMM模型
# 复制数据集df3到df_GMM
df_GMM = df3.copy()
# 复制数据集blob_df到df_blob_GMM
df_blob_GMM = blob_df.copy()
# 复制数据集dart_df到df_dart_GMM
df_dart_GMM = dart_df.copy()
# 复制数据集basic2_df到df_basic2_GMM
df_basic2_GMM = basic2_df.copy()
# 复制数据集outliers_df到df_outliers_GMM
df_outliers_GMM = outliers_df.copy()
# 复制数据集spiral2_df到df_spiral2_GMM
df_spiral2_GMM = spiral2_df.copy()
# 复制数据集boxes3_df到df_boxes3_GMM
df_boxes3_GMM = boxes3_df.copy()
# 给df_blob_GMM数据框删除'color'列
df_blob_GMM.drop(['color'], axis=1, inplace=True)
# 给df_dart_GMM数据框删除'color'列
df_dart_GMM.drop(['color'], axis=1, inplace=True)
# 给df_basic2_GMM数据框删除'color'列
df_basic2_GMM.drop(['color'], axis=1, inplace=True)
# 给df_outliers_GMM数据框删除'color'列
df_outliers_GMM.drop(['color'], axis=1, inplace=True)
# 给df_spiral2_GMM数据框删除'color'列
df_spiral2_GMM.drop(['color'], axis=1, inplace=True)
# 给df_boxes3_GMM数据框删除'color'列
df_boxes3_GMM.drop(['color'], axis=1, inplace=True)
# 导入所需的库
from sklearn.mixture import GaussianMixture
# 创建一个高斯混合模型对象,指定模型的分量数量为8
gmm = GaussianMixture(n_components=8)
# 使用高斯混合模型对数据进行拟合和预测,得到预测结果
y_GMM = gmm.fit_predict(df_GMM)
# 创建高斯混合模型对象,指定模型的分量数量为4
GMM_blob = GaussianMixture(n_components=4)
# 使用高斯混合模型对数据进行拟合和预测,得到预测结果
y_GMM_blob = GMM_blob.fit_predict(df_blob_GMM)
# 创建高斯混合模型对象,指定模型的分量数量为2
GMM_dart = GaussianMixture(n_components=2)
# 使用高斯混合模型对数据进行拟合和预测,得到预测结果
y_GMM_dart = GMM_dart.fit_predict(df_dart_GMM)
# 创建高斯混合模型对象,指定模型的分量数量为5
GMM_basic = GaussianMixture(n_components=5)
# 使用高斯混合模型对数据进行拟合和预测,得到预测结果
y_GMM_basic = GMM_basic.fit_predict(df_basic2_GMM)
# 创建高斯混合模型对象,指定模型的分量数量为3
GMM_outliers = GaussianMixture(n_components=3)
# 使用高斯混合模型对数据进行拟合和预测,得到预测结果
y_GMM_outliers = GMM_outliers.fit_predict(df_outliers_GMM)
# 创建高斯混合模型对象,指定模型的分量数量为2
GMM_spiral2 = GaussianMixture(n_components=2)
# 使用高斯混合模型对数据进行拟合和预测,得到预测结果
y_GMM_spiral2 = GMM_spiral2.fit_predict(df_spiral2_GMM)
# 创建高斯混合模型对象,指定模型的分量数量为12
GMM_boxes3 = GaussianMixture(n_components=12)
# 使用高斯混合模型对数据进行拟合和预测,得到预测结果
y_GMM_boxes3 = GMM_boxes3.fit_predict(df_boxes3_GMM)
# 在数据集df_blob_GMM中创建一个名为"Cluster"的列
df_blob_GMM['Cluster'] = y_GMM_blob
# 将GMM聚类算法的结果y_GMM_blob赋值给df_blob_GMM数据集的"Cluster"列
# 在数据集df_dart_GMM中创建一个名为"Cluster"的列
df_dart_GMM['Cluster'] = y_GMM_dart
# 将GMM聚类算法的结果y_GMM_dart赋值给df_dart_GMM数据集的"Cluster"列
# 在数据集df_basic2_GMM中创建一个名为"Cluster"的列
df_basic2_GMM['Cluster'] = y_GMM_basic
# 将GMM聚类算法的结果y_GMM_basic赋值给df_basic2_GMM数据集的"Cluster"列
# 在数据集df_outliers_GMM中创建一个名为"Cluster"的列
df_outliers_GMM['Cluster'] = y_GMM_outliers
# 将GMM聚类算法的结果y_GMM_outliers赋值给df_outliers_GMM数据集的"Cluster"列
# 在数据集df_spiral2_GMM中创建一个名为"Cluster"的列
df_spiral2_GMM['Cluster'] = y_GMM_spiral2
# 将GMM聚类算法的结果y_GMM_spiral2赋值给df_spiral2_GMM数据集的"Cluster"列
# 在数据集df_boxes3_GMM中创建一个名为"Cluster"的列
df_boxes3_GMM['Cluster'] = y_GMM_boxes3
# 将GMM聚类算法的结果y_GMM_boxes3赋值给df_boxes3_GMM数据集的"Cluster"列
7.4 比较结果
# 创建子图fig, axes,其中nrows=6表示子图行数为6,ncols=2表示子图列数为2,figsize=(10,30)表示整个图的大小为10*30
fig, axes = plt.subplots(nrows=6, ncols=2, figsize=(10,30))
# 设置整个图的标题为'ANSWER vs GMM clustering\n',字体大小为18
fig.suptitle('ANSWER vs GMM clustering\n', size = 18)
# 绘制第一个子图,显示Answer Blob的散点图,其中x、y、color分别表示数据的横坐标、纵坐标和颜色,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[0,0].scatter(blob_df['x'], blob_df['y'], c=blob_df['color'], s=10, cmap = "Set3")
axes[0,0].set_title("Answer Blob") # 设置子图标题为"Answer Blob"
# 绘制第二个子图,显示GMM clustering Blob的散点图,其中x、y、Cluster分别表示数据的横坐标、纵坐标和聚类结果,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[0,1].scatter(df_blob_GMM['x'], df_blob_GMM['y'], c=df_blob_GMM['Cluster'], s=10, cmap = "Set3")
axes[0,1].set_title("GMM clustering Blob") # 设置子图标题为"GMM clustering Blob"
# 绘制第三个子图,显示Answer Dart的散点图,其中x、y、color分别表示数据的横坐标、纵坐标和颜色,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[1,0].scatter(dart_df['x'], dart_df['y'], c=dart_df['color'], s=10, cmap = "Set3")
axes[1,0].set_title("Answer Dart") # 设置子图标题为"Answer Dart"
# 绘制第四个子图,显示GMM clustering Dart的散点图,其中x、y、Cluster分别表示数据的横坐标、纵坐标和聚类结果,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[1,1].scatter(df_dart_GMM['x'], df_dart_GMM['y'], c=df_dart_GMM['Cluster'], s=10, cmap = "Set3")
axes[1,1].set_title("GMM clustering Dart") # 设置子图标题为"GMM clustering Dart"
# 绘制第五个子图,显示Answer Basic的散点图,其中x、y、color分别表示数据的横坐标、纵坐标和颜色,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[2,0].scatter(basic2_df['x'], basic2_df['y'], c=basic2_df['color'], s=10, cmap = "Set3")
axes[2,0].set_title("Answer Basic") # 设置子图标题为"Answer Basic"
# 绘制第六个子图,显示GMM clustering Basic的散点图,其中x、y、Cluster分别表示数据的横坐标、纵坐标和聚类结果,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[2,1].scatter(df_basic2_GMM['x'], df_basic2_GMM['y'], c=df_basic2_GMM['Cluster'], s=10, cmap = "Set3")
axes[2,1].set_title("GMM clustering Basic") # 设置子图标题为"GMM clustering Basic"
# 绘制第七个子图,显示Answer Outliers的散点图,其中x、y、color分别表示数据的横坐标、纵坐标和颜色,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[3,0].scatter(outliers_df['x'], outliers_df['y'], c=outliers_df['color'], s=10, cmap = "Set3")
axes[3,0].set_title("Answer Outliers") # 设置子图标题为"Answer Outliers"
# 绘制第八个子图,显示GMM clustering Outliers的散点图,其中x、y、Cluster分别表示数据的横坐标、纵坐标和聚类结果,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[3,1].scatter(df_outliers_GMM['x'], df_outliers_GMM['y'], c=df_outliers_GMM['Cluster'], s=10, cmap = "Set3")
axes[3,1].set_title("GMM clustering Outliers") # 设置子图标题为"GMM clustering Outliers"
# 绘制第九个子图,显示Answer Spiral的散点图,其中x、y、color分别表示数据的横坐标、纵坐标和颜色,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[4,0].scatter(spiral2_df['x'], spiral2_df['y'], c=spiral2_df['color'], s=10, cmap = "Set3")
axes[4,0].set_title("Answer Spiral") # 设置子图标题为"Answer Spiral"
# 绘制第十个子图,显示GMM clustering Spiral的散点图,其中x、y、Cluster分别表示数据的横坐标、纵坐标和聚类结果,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[4,1].scatter(df_spiral2_GMM['x'], df_spiral2_GMM['y'], c=df_spiral2_GMM['Cluster'], s=10, cmap = "Set3")
axes[4,1].set_title("GMM clustering Spiral") # 设置子图标题为"GMM clustering Spiral"
# 绘制第十一个子图,显示Answer Boxes的散点图,其中x、y、color分别表示数据的横坐标、纵坐标和颜色,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[5,0].scatter(boxes3_df['x'], boxes3_df['y'], c=boxes3_df['color'], s=10, cmap = "Set3")
axes[5,0].set_title("Answer Boxes") # 设置子图标题为"Answer Boxes"
# 绘制第十二个子图,显示GMM clustering Boxes的散点图,其中x、y、Cluster分别表示数据的横坐标、纵坐标和聚类结果,s=10表示散点的大小为10,cmap="Set3"表示使用Set3颜色映射
axes[5,1].scatter(df_boxes3_GMM['x'], df_boxes3_GMM['y'], c=df_boxes3_GMM['Cluster'], s=10, cmap = "Set3")
axes[5,1].set_title("GMM clustering Boxes") # 设置子图标题为"GMM clustering Boxes"
# 调整子图的布局
plt.tight_layout()

在线零售数据上的7.5 GMM聚类模型
# 将df2复制给df_GMM,因为我们需要引用之前的df来添加聚类编号
df_GMM = df2.copy()
# 检查每个聚类中的项数,并创建一个名为'Cluster'的列
df_GMM['Cluster'] = y_GMM
# 统计每个聚类中的项数,并显示出来
df_GMM['Cluster'].value_counts()
0 1165
3 1011
7 543
2 367
6 311
5 253
4 149
1 105
Name: Cluster, dtype: int64
# 设置图形的大小
plt.figure(figsize=(15,7))
# 绘制散点图
sns.scatterplot(data=df_GMM, x='Amount', y='Frequency', hue='Cluster', s=15, palette="Set3")
# 参数说明:
# data:要绘制的数据集
# x:x轴的数据列
# y:y轴的数据列
# hue:根据该列的值对数据点进行着色
# s:数据点的大小
# palette:颜色调色板,用于设置数据点的颜色
<AxesSubplot:xlabel='Amount', ylabel='Frequency'>

8. 所有算法比较
# 创建子图fig, axes = plt.subplots(nrows=6, ncols=5,figsize=(30,30))
# 创建一个6行5列的子图,设置整个图的大小为30x30
# 设置总标题fig.suptitle('ANSWER vs different algorithm\n', size = 18)
# 设置总标题为'ANSWER vs different algorithm',字体大小为18
# 绘制Answer Blob散点图
axes[0,0].scatter(blob_df['x'], blob_df['y'], c=blob_df['color'], s=10, cmap = "Set3")
# 在第1行第1列的子图中绘制Answer Blob的散点图
# x轴数据为blob_df的x列,y轴数据为blob_df的y列,颜色根据color列的值确定,点的大小为10,颜色映射为"Set3"
axes[0,0].set_title("Answer Blob")
# 设置该子图的标题为"Answer Blob"
# 绘制GMM clustering Blob散点图
axes[0,1].scatter(df_blob_GMM['x'], df_blob_GMM['y'], c=df_blob_GMM['Cluster'], s=10, cmap = "Set3")
# 在第1行第2列的子图中绘制GMM clustering Blob的散点图
# x轴数据为df_blob_GMM的x列,y轴数据为df_blob_GMM的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[0,1].set_title("GMM clustering Blob")
# 设置该子图的标题为"GMM clustering Blob"
# 绘制K-Means Blob散点图
axes[0,2].scatter(df_blob_kmeans['x'], df_blob_kmeans['y'], c=df_blob_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第1行第3列的子图中绘制K-Means Blob的散点图
# x轴数据为df_blob_kmeans的x列,y轴数据为df_blob_kmeans的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[0,2].set_title("K-Means Blob")
# 设置该子图的标题为"K-Means Blob"
# 绘制Hierarchical clustering Blob散点图
axes[0,3].scatter(df_blob_AgglomerativeC['x'], df_blob_AgglomerativeC['y'], c=df_blob_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第1行第4列的子图中绘制Hierarchical clustering Blob的散点图
# x轴数据为df_blob_AgglomerativeC的x列,y轴数据为df_blob_AgglomerativeC的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[0,3].set_title("Hierarchical clustering Blob")
# 设置该子图的标题为"Hierarchical clustering Blob"
# 绘制DBSCAN clustering Blob散点图
axes[0,4].scatter(df_blob_DBScan['x'], df_blob_DBScan['y'], c=df_blob_DBScan['Cluster'], s=10, cmap = "Set3")
# 在第1行第5列的子图中绘制DBSCAN clustering Blob的散点图
# x轴数据为df_blob_DBScan的x列,y轴数据为df_blob_DBScan的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[0,4].set_title("DBSCAN clustering Blob")
# 设置该子图的标题为"DBSCAN clustering Blob"
# 绘制Answer Dart散点图
axes[1,0].scatter(dart_df['x'], dart_df['y'], c=dart_df['color'], s=10, cmap = "Set3")
# 在第2行第1列的子图中绘制Answer Dart的散点图
# x轴数据为dart_df的x列,y轴数据为dart_df的y列,颜色根据color列的值确定,点的大小为10,颜色映射为"Set3"
axes[1,0].set_title("Answer Dart")
# 设置该子图的标题为"Answer Dart"
# 绘制GMM clustering Dart散点图
axes[1,1].scatter(df_dart_GMM['x'], df_dart_GMM['y'], c=df_dart_GMM['Cluster'], s=10, cmap = "Set3")
# 在第2行第2列的子图中绘制GMM clustering Dart的散点图
# x轴数据为df_dart_GMM的x列,y轴数据为df_dart_GMM的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[1,1].set_title("GMM clustering Dart")
# 设置该子图的标题为"GMM clustering Dart"
# 绘制K-Means Dart散点图
axes[1,2].scatter(df_dart_kmeans['x'], df_dart_kmeans['y'], c=df_dart_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第2行第3列的子图中绘制K-Means Dart的散点图
# x轴数据为df_dart_kmeans的x列,y轴数据为df_dart_kmeans的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[1,2].set_title("K-Means Dart")
# 设置该子图的标题为"K-Means Dart"
# 绘制Hierarchical clustering Dart散点图
axes[1,3].scatter(df_dart_AgglomerativeC['x'], df_dart_AgglomerativeC['y'], c=df_dart_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第2行第4列的子图中绘制Hierarchical clustering Dart的散点图
# x轴数据为df_dart_AgglomerativeC的x列,y轴数据为df_dart_AgglomerativeC的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[1,3].set_title("Hierarchical clustering Dart")
# 设置该子图的标题为"Hierarchical clustering Dart"
# 绘制DBSCAN clustering Dart散点图
axes[1,4].scatter(df_dart_DBScan['x'], df_dart_DBScan['y'], c=df_dart_DBScan['Cluster'], s=10, cmap = "Set3")
# 在第2行第5列的子图中绘制DBSCAN clustering Dart的散点图
# x轴数据为df_dart_DBScan的x列,y轴数据为df_dart_DBScan的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[1,4].set_title("DBSCAN clustering Dart")
# 设置该子图的标题为"DBSCAN clustering Dart"
# 绘制Answer Basic散点图
axes[2,0].scatter(basic2_df['x'], basic2_df['y'], c=basic2_df['color'], s=10, cmap = "Set3")
# 在第3行第1列的子图中绘制Answer Basic的散点图
# x轴数据为basic2_df的x列,y轴数据为basic2_df的y列,颜色根据color列的值确定,点的大小为10,颜色映射为"Set3"
axes[2,0].set_title("Answer Basic")
# 设置该子图的标题为"Answer Basic"
# 绘制GMM clustering Basic散点图
axes[2,1].scatter(df_basic2_GMM['x'], df_basic2_GMM['y'], c=df_basic2_GMM['Cluster'], s=10, cmap = "Set3")
# 在第3行第2列的子图中绘制GMM clustering Basic的散点图
# x轴数据为df_basic2_GMM的x列,y轴数据为df_basic2_GMM的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[2,1].set_title("GMM clustering Basic")
# 设置该子图的标题为"GMM clustering Basic"
# 绘制K-Means Basic散点图
axes[2,2].scatter(df_basic_kmeans['x'], df_basic_kmeans['y'], c=df_basic_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第3行第3列的子图中绘制K-Means Basic的散点图
# x轴数据为df_basic_kmeans的x列,y轴数据为df_basic_kmeans的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[2,2].set_title("K-Means Basic")
# 设置该子图的标题为"K-Means Basic"
# 绘制Hierarchical clustering Basic散点图
axes[2,3].scatter(df_basic2_AgglomerativeC['x'], df_basic2_AgglomerativeC['y'], c=df_basic2_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第3行第4列的子图中绘制Hierarchical clustering Basic的散点图
# x轴数据为df_basic2_AgglomerativeC的x列,y轴数据为df_basic2_AgglomerativeC的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[2,3].set_title("Hierarchical clustering Basic")
# 设置该子图的标题为"Hierarchical clustering Basic"
# 绘制DBSCAN clustering Basic散点图
axes[2,4].scatter(df_basic2_DBScan['x'], df_basic2_DBScan['y'], c=df_basic2_DBScan['Cluster'], s=10, cmap = "Set3")
# 在第3行第5列的子图中绘制DBSCAN clustering Basic的散点图
# x轴数据为df_basic2_DBScan的x列,y轴数据为df_basic2_DBScan的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[2,4].set_title("DBSCAN clustering Basic")
# 设置该子图的标题为"DBSCAN clustering Basic"
# 绘制Answer Outliers散点图
axes[3,0].scatter(outliers_df['x'], outliers_df['y'], c=outliers_df['color'], s=10, cmap = "Set3")
# 在第4行第1列的子图中绘制Answer Outliers的散点图
# x轴数据为outliers_df的x列,y轴数据为outliers_df的y列,颜色根据color列的值确定,点的大小为10,颜色映射为"Set3"
axes[3,0].set_title("Answer Outliers")
# 设置该子图的标题为"Answer Outliers"
# 绘制GMM clustering Outliers散点图
axes[3,1].scatter(df_outliers_GMM['x'], df_outliers_GMM['y'], c=df_outliers_GMM['Cluster'], s=10, cmap = "Set3")
# 在第4行第2列的子图中绘制GMM clustering Outliers的散点图
# x轴数据为df_outliers_GMM的x列,y轴数据为df_outliers_GMM的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[3,1].set_title("GMM clustering Outliers")
# 设置该子图的标题为"GMM clustering Outliers"
# 绘制K-Means Outliers散点图
axes[3,2].scatter(df_outliers_kmeans['x'], df_outliers_kmeans['y'], c=df_outliers_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第4行第3列的子图中绘制K-Means Outliers的散点图
# x轴数据为df_outliers_kmeans的x列,y轴数据为df_outliers_kmeans的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[3,2].set_title("K-Means Outliers")
# 设置该子图的标题为"K-Means Outliers"
# 绘制Hierarchical clustering Outliers散点图
axes[3,3].scatter(df_outliers_AgglomerativeC['x'], df_outliers_AgglomerativeC['y'], c=df_outliers_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第4行第4列的子图中绘制Hierarchical clustering Outliers的散点图
# x轴数据为df_outliers_AgglomerativeC的x列,y轴数据为df_outliers_AgglomerativeC的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[3,3].set_title("Hierarchical clustering Outliers")
# 设置该子图的标题为"Hierarchical clustering Outliers"
# 绘制DBSCAN clustering Outliers散点图
axes[3,4].scatter(df_outliers_DBScan['x'], df_outliers_DBScan['y'], c=df_outliers_DBScan['Cluster'], s=10, cmap = "Set3")
# 在第4行第5列的子图中绘制DBSCAN clustering Outliers的散点图
# x轴数据为df_outliers_DBScan的x列,y轴数据为df_outliers_DBScan的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[3,4].set_title("DBSCAN clustering Outliers")
# 设置该子图的标题为"DBSCAN clustering Outliers"
# 绘制Answer Spiral散点图
axes[4,0].scatter(spiral2_df['x'], spiral2_df['y'], c=spiral2_df['color'], s=10, cmap = "Set3")
# 在第5行第1列的子图中绘制Answer Spiral的散点图
# x轴数据为spiral2_df的x列,y轴数据为spiral2_df的y列,颜色根据color列的值确定,点的大小为10,颜色映射为"Set3"
axes[4,0].set_title("Answer Spiral")
# 设置该子图的标题为"Answer Spiral"
# 绘制GMM clustering Spiral散点图
axes[4,1].scatter(df_spiral2_GMM['x'], df_spiral2_GMM['y'], c=df_spiral2_GMM['Cluster'], s=10, cmap = "Set3")
# 在第5行第2列的子图中绘制GMM clustering Spiral的散点图
# x轴数据为df_spiral2_GMM的x列,y轴数据为df_spiral2_GMM的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[4,1].set_title("GMM clustering Spiral")
# 设置该子图的标题为"GMM clustering Spiral"
# 绘制K-Means Spiral散点图
axes[4,2].scatter(df_spiral2_kmeans['x'], df_spiral2_kmeans['y'], c=df_spiral2_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第5行第3列的子图中绘制K-Means Spiral的散点图
# x轴数据为df_spiral2_kmeans的x列,y轴数据为df_spiral2_kmeans的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[4,2].set_title("K-Means Spiral")
# 设置该子图的标题为"K-Means Spiral"
# 绘制Hierarchical clustering Spiral散点图
axes[4,3].scatter(df_spiral2_AgglomerativeC['x'], df_spiral2_AgglomerativeC['y'], c=df_spiral2_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第5行第4列的子图中绘制Hierarchical clustering Spiral的散点图
# x轴数据为df_spiral2_AgglomerativeC的x列,y轴数据为df_spiral2_AgglomerativeC的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[4,3].set_title("Hierarchical clustering Spiral")
# 设置该子图的标题为"Hierarchical clustering Spiral"
# 绘制DBSCAN clustering Spiral散点图
axes[4,4].scatter(df_spiral2_DBScan['x'], df_spiral2_DBScan['y'], c=df_spiral2_DBScan['Cluster'], s=10, cmap = "Set3")
# 在第5行第5列的子图中绘制DBSCAN clustering Spiral的散点图
# x轴数据为df_spiral2_DBScan的x列,y轴数据为df_spiral2_DBScan的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[4,4].set_title("DBSCAN clustering Spiral")
# 设置该子图的标题为"DBSCAN clustering Spiral"
# 绘制Answer Boxes散点图
axes[5,0].scatter(boxes3_df['x'], boxes3_df['y'], c=boxes3_df['color'], s=10, cmap = "Set3")
# 在第6行第1列的子图中绘制Answer Boxes的散点图
# x轴数据为boxes3_df的x列,y轴数据为boxes3_df的y列,颜色根据color列的值确定,点的大小为10,颜色映射为"Set3"
axes[5,0].set_title("Answer Boxes")
# 设置该子图的标题为"Answer Boxes"
# 绘制GMM clustering Boxes散点图
axes[5,1].scatter(df_boxes3_GMM['x'], df_boxes3_GMM['y'], c=df_boxes3_GMM['Cluster'], s=10, cmap = "Set3")
# 在第6行第2列的子图中绘制GMM clustering Boxes的散点图
# x轴数据为df_boxes3_GMM的x列,y轴数据为df_boxes3_GMM的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[5,1].set_title("GMM clustering Boxes")
# 设置该子图的标题为"GMM clustering Boxes"
# 绘制K-Means Boxes散点图
axes[5,2].scatter(df_boxes3_kmeans['x'], df_boxes3_kmeans['y'], c=df_boxes3_kmeans['Cluster'], s=10, cmap = "Set3")
# 在第6行第3列的子图中绘制K-Means Boxes的散点图
# x轴数据为df_boxes3_kmeans的x列,y轴数据为df_boxes3_kmeans的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[5,2].set_title("K-Means Boxes")
# 设置该子图的标题为"K-Means Boxes"
# 绘制Hierarchical clustering Boxes散点图
axes[5,3].scatter(df_boxes3_AgglomerativeC['x'], df_boxes3_AgglomerativeC['y'], c=df_boxes3_AgglomerativeC['Cluster'], s=10, cmap = "Set3")
# 在第6行第4列的子图中绘制Hierarchical clustering Boxes的散点图
# x轴数据为df_boxes3_AgglomerativeC的x列,y轴数据为df_boxes3_AgglomerativeC的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[5,3].set_title("Hierarchical clustering Boxes")
# 设置该子图的标题为"Hierarchical clustering Boxes"
# 绘制DBSCAN clustering Boxes散点图
axes[5,4].scatter(df_boxes3_DBScan['x'], df_boxes3_DBScan['y'], c=df_boxes3_DBScan['Cluster'], s=10, cmap = "Set3")
# 在第6行第5列的子图中绘制DBSCAN clustering Boxes的散点图
# x轴数据为df_boxes3_DBScan的x列,y轴数据为df_boxes3_DBScan的y列,颜色根据Cluster列的值确定,点的大小为10,颜色映射为"Set3"
axes[5,4].set_title("DBSCAN clustering Boxes")
# 设置该子图的标题为"DBSCAN clustering Boxes"
# 调整子图布局
plt.tight_layout()
# 调整子图的布局,使得子图之间的间距合适,防止重叠

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- c语言之将输入的十进制转换成二进制数并打印原码反码补码
- 某国产沙盒游戏的启动器逆向
- 技术写作:漏斗内容策略、认知博客、支柱内容、研究报告、通用门控内容、电子书和教程
- PYTHON基础:SVM不同核函数的区别与选择
- PTA——闰年判断
- 八、W5100S/W5500+RP2040之MicroPython开发<HTTP Server示例>
- Android Studio 报错The project uses Gradle 4.4 which is incompatible with Java 11 or newer.!
- 【EI会议征稿通知】第五届计算机信息和大数据应用国际学术会议(CIBDA 2024)
- CSS从入门到精通(5)
- PostgreSQL帮助、用户、权限操作