AtCoder Beginner Contest 335 (Sponsored by Mynavi) G. Discrete Logarithm Problems（群论的阶 拉格朗日定理）

题目

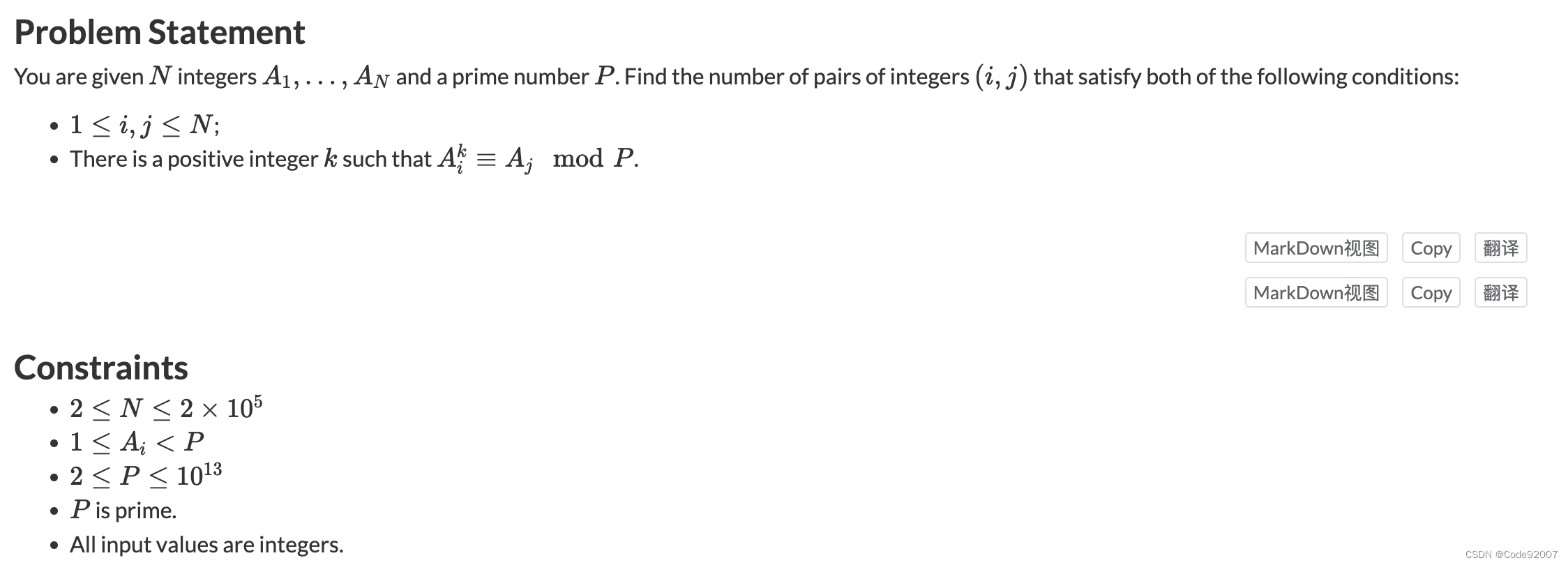
n(n<=2e5)个数，第i个数ai(ai<p)，给定质数p(2<=p<=1e13)

求存在正整数k，使得成立的(i,j)(1<=i,j<=n)对数

思路来源

官方题解

heltion代码

题解

赛中搞了原根+bsgs一大堆，后来发现根本没必要

结论

称满足的最小正整数x为a的阶，记作

若，则方程有解

拉格朗日定理

若，有

感性证明

感觉无需深究，当原根/群论的一个性质记就可以

方法论

试除法，找到每个ai的阶，

即如果除掉一个素因子x后还成立，就除掉一个素因子

得到每个数的阶后，1e13以内的数的约数最大1e4，但实际没有那么多

还有阶为x的恰有phi(x)个这样的限制

暴力n^2遍历约数即可，这里带了个map的log也过了

代码

#include<bits/stdc++.h>
using namespace std;
// #include<random>
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
#define LL long long
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef long long ll;
#define LL __int128
const int N=2e5+10;
ll p,a[N],d;
int n;
vector<ll>fac;
map<ll,ll>now;
ll modpow(ll x,ll n,ll mod){
    ll res=1;
    for(;n;n>>=1,x=(LL)x*x%mod){
        if(n&1)res=(LL)res*x%mod;
    }
    return res;
}
int main(){
    scanf("%d%lld",&n,&p);
    rep(i,1,n){
        scanf("%lld",&a[i]);
    }
    d=p-1;
    for(ll i=2;i*i<=d;++i){
        if(d%i==0){
            fac.pb(i);
            while(d%i==0)d/=i;
        }
    }
    if(d>1)fac.pb(d);
    rep(i,1,n){
        ll d=p-1;
        for(auto &x:fac){
            while(d%x==0 && modpow(a[i],d/x,p)==1){
                d/=x;
            }
        }
        now[d]++;
        //printf("i:%d d:%lld\n",i,d);
    }
    ll ans=0;
    for(auto &x:now){
        for(auto &y:now){
            if(x.fi%y.fi==0){
                ans+=1ll*x.se*y.se;
            }
        }
    }
    printf("%lld\n",ans);
    return 0;
}