机器学习_捕捉函数的变化趋势(凸函数)
机器学习所关心的问题之一捕捉函数的变化趋势,也就是标签(y)是如何随着特征字段(x)而变化的,这个变化趋势是通过求导和微分来实现的。
连续性是求导的前提条件
具有连续性的函数,y值随x值的变化是连贯不间断的。
并不是所有函数都具有连续性,像上面提到的阶跃函数从-1到1的跃迁明显就不具有连续性。
通过求导发现 y 如何随 x 而变
导数是定义在连续函数的基础之上的。想要对函数求导,函数至少要有一段是连续的。
当A点和B点的距离越来越小,两个点无限接近,逼近极限的时候,在即将重合而又未重合的一刹那,割线就变成切线了,如下图所示:
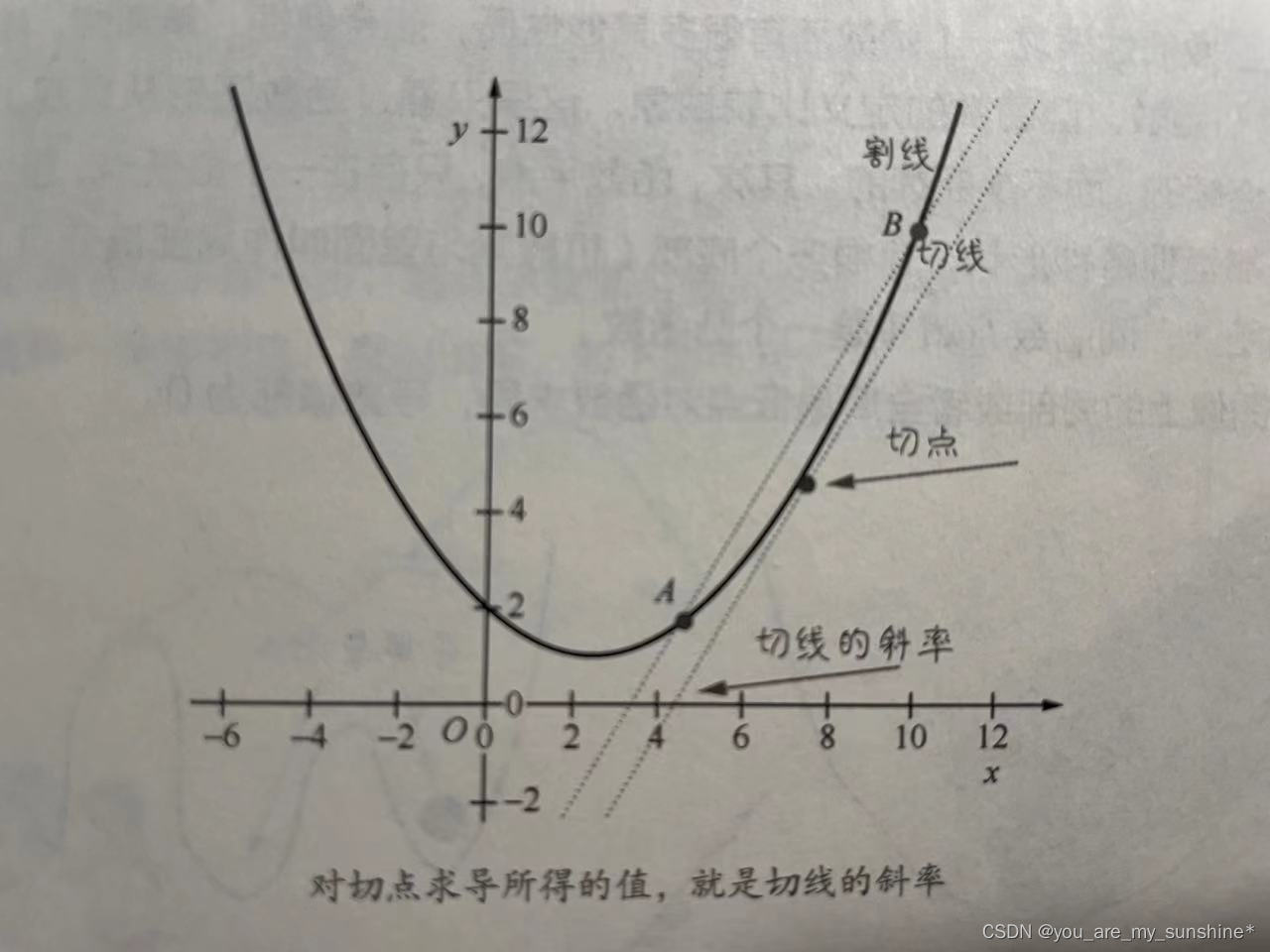
而此时,对切点求导所得的值,就是切线的斜率。
- 当斜率为正的时候,说明函数目前变化趋势是在上升。
- 当斜率为负的时候,说明函数目前变化趋势是在下降。
- 当斜率为0的时候,说明函数正处于全局或者局部的最低点,趋势即将发生改变。
总结:函数变化的趋势至少由两个点体现,即当A趋近于B的时候,求其变换的极限,这就是导数。导数的值和它附近的一小段连续函数有关。如果没有那么一段连续的函数,就无法计算其切线的斜率,函数在该点也就是不可导的。
通过求导,实现了以直代曲,也发现了y值随x值而变化的方向。引申到机器学习领域,通过导数就可以得到标签y随特征x而变化的方向。
导数是针对一个变量而言的变化趋向。而对于多元(即多变量)的函数,他关于其中一个变量的导数为偏导数,此时保持其他变量恒定。如果其中所有变量都允许变化,则成为全导数。
凸函数有一个全局最低点
凸函数的定义比较抽象,这里指通过函数徒刑从直观上去理解。首先,函数形状必须是连续的,而不是断续的。其次,函数平滑,只存在一个最低点,整个函数呈现碗状。而非凸函数,困难呈现各种形状,有很多个底部(机器学习里面叫作局部最低点)。下图所示的函数f1就是一个凸函数,而函数f2就不是一个凸函数。
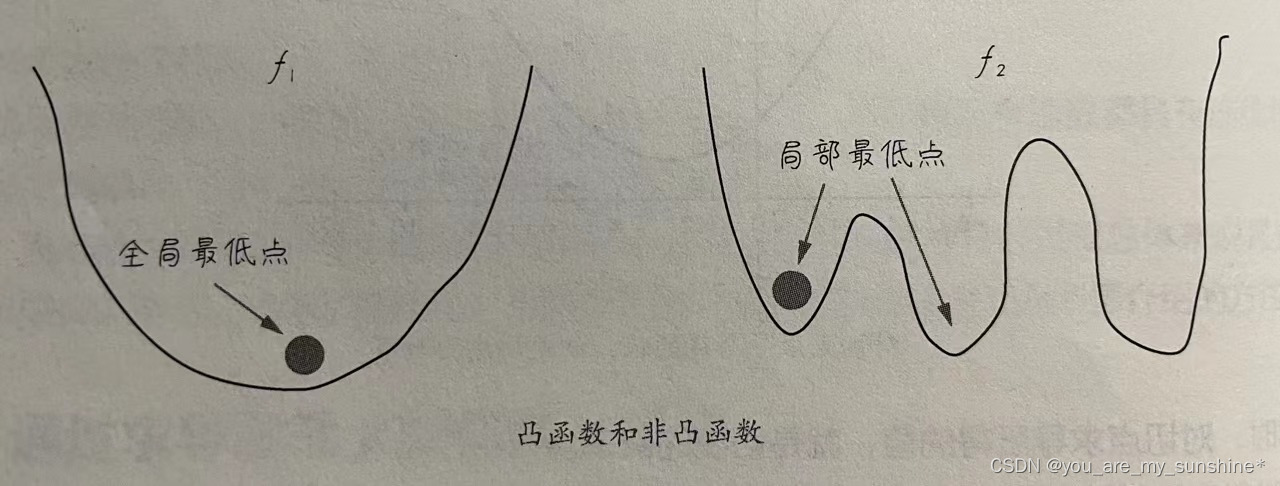
图说:凸函数的小球不管初始化位置放在哪里,都可以沿着导数给出的方向滚到最低点;而非凸函数中,小球就可能卡在半路,也就是局部最低点。在机器学习中,无法到达全局最低点是很不理想的。
在连续函数图像上的局部或者全局最低点对函数求导,导数值都为0。
正是因为只有凸函数能够确保降到全局最低点,所以用在机器学习的梯度下降过程中。
学习机器学习的参考资料:
(1)书籍
利用Python进行数据分析
西瓜书
百面机器学习
机器学习实战
阿里云天池大赛赛题解析(机器学习篇)
白话机器学习中的数学
零基础学机器学习
图解机器学习算法
…
(2)机构
光环大数据
开课吧
极客时间
七月在线
深度之眼
贪心学院
拉勾教育
博学谷
…
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!