深度剖析C语言数据在类型中的存储之浮点型在内存中的存储

目录

1.对浮点数的初步认识

?1.1浮点数的表示范围：

?2.用一个题的例子来引入对浮点数存储的探讨

3(重点）浮点数的存储规则?

4.对例子答案的解释?

---

?

1.对浮点数的初步认识

浮点数就是我们口头的小数

常见的浮点数如：3.14等

另外的浮点数的表达：1E10(这种表示方法常用在Python中，E表示次方的意思，该数表示1.0*10^10

C语言中浮点数家族包括：float（大小为2个字节），double，大小为8个字节等

?1.1浮点数的表示范围：

?2.用一个题的例子来引入对浮点数存储的探讨

我们来猜一下下面这段代码的执行结果：

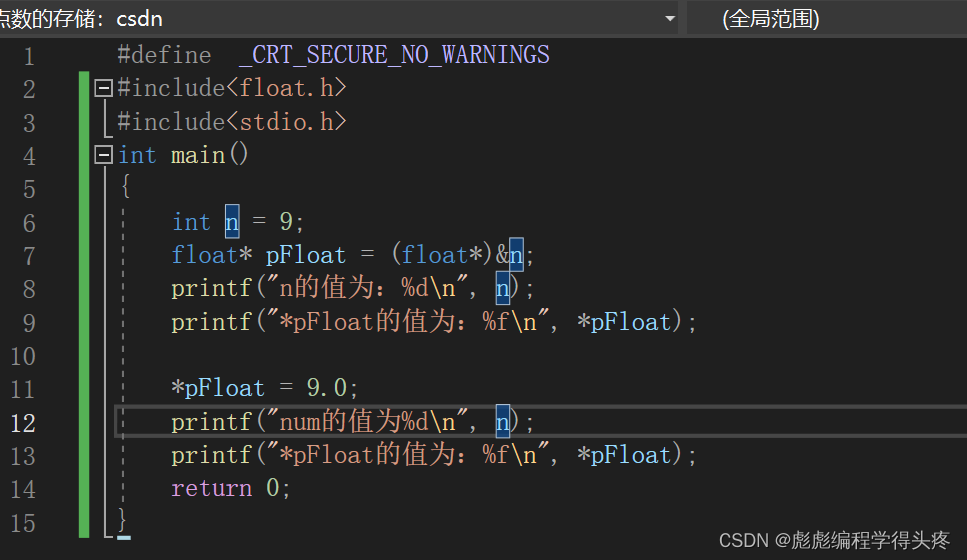
根据前面的内容，我想很多伙伴给出的答案应该是：9、9.0、9、 9.0

好我们来看一下运行结果是怎么样的。

附上源码，大家运行看一下体验一下：

#include<float.h>
#include<stdio.h>
int main()
{
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);

	*pFloat = 9.0;
	printf("num的值为%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	return 0;
}

二和三的答案为什么和我们预算的不一样呢，那就说明一个问题：

说明整形和浮点型在内存中的存储是有差异的。

那么浮点型在内存中是如何存储的，又是如何导致结果和我们预想的不一样呢，看官请注意接下来的重点内容了

3(重点）浮点数的存储规则?

在上面的例子中我们提出疑问：

n 和*pFloat明明是同一个数，为什么浮点数和整数的解读结果的差别会如此之大呢。

那么要解决这个问题，就要搞懂浮点数在计算机内部的存储方法：

根据国际标准IEEE（电气和电子工程协会）754，任意一个二进制浮点数V都可以表示成下面的形式：

• （-1）^S*M*2^E
• (-1)^S表示符号位，当S = 0，V为正数；当S=1,V为负数
• M表示有效数字，大于等于1小于等于2
• 2^E表示指数位?

在进入举例子理解之前，给大家先复习一下数位进位知识：

那么对于一个二进制整数和二进制浮点数来说：

有了上面的铺垫，我们来举例子来理解一下标准：

例如十进制的5.5，写成二进制的序列就是101.1，那么用科学计数法可以表示为1.011*2^2（相当于小数点向左移动了两位）?

按照标准的形式我们可以得出5.5在标准中的

S = 0(因为是正数）M = 1.011 E = 2

接着，就是存储的部分规定：

IEEE 754规定：

对于32位的浮点数（float 大小为4个字节）?，最高的1位存储的符号位S,接着的8个比特位存储的是指数E.

图解：

IEEE 754规定 ：
对于32位的浮点数，最高的1位是符号位S，接着的8位指数E，剩下的23位为有效数字为M

?

对于64位的浮点数(double),最高的1位是符号位S,接下来的11位是指数E,剩下的52位为有效数字M?

?

同时值得注意的是：IEEE 754对有效数字M和E的存储还有一些特别的规定。

①：在前面的内容中我们说过，1<=M<2,也就是说M可以写成1.xxxxx的形式，xxxx表示小数部分，例如5.5二进制表示后其M可以写成1.011.那么IEEE754规定，在计算机内部保存M的时候，默认这个数的第一位总是1，因此可以被舍去，只保存后面xxxxx的部分，比如保存1.011的时候就只保存011，读取的时候再把第一位的1加上去。

这样做的目的和好处就是：节省了一位有效数字，以32位浮点数为例，留给M只有23位，将第一位的1舍弃过后，相当于m现在可以多存储小数点后一位的数据就相当于保存了24为数字，精度就更高了。

②：对于指数E,首先，E为一个无符号整数（unsigned?int）这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的取值范围为0~2047。

但是，我们知道，科学计数法中的E是可以出现负数的(比如0.00011）E的值就为-4

所以IEEE?754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

?

对于E从内存中取出：分为三种情况：

①E不全为0或者不全为1（大多数情况）

这种情况就是怎么存入就逆向取出就行既：指数E的计算值减去127（或1023），得到真实指数值，然后将有效数字M前加上第一位1，

比如：0.5在内存中的存储形式：

0.5的二进制序列是：0.1，用科学计数法表示完整就是（-1）^0*1.0*2^-1

S = 0 M = 1.0 E = -1

那么按照存储规则来说：

第一位存0符号位

接下来八位1存E:要加上中间数127：-1+127 = 126，这八个比特位就存126的二进制编码

接下来的23位存M:但是要忽略第一位的1，去掉为01，补齐23位的0

那么得到存储的二进制序列为：

0 01111110 00000000000000000000000

0.5是整数，原码，反码补码相同，就存储上面这个序列。

换成16进制就是

ox 3f 00 00 00,我们来看一下：

?

②E全为0

这时说明原来的指数（因为存储要加中间数）是-127或者-1023，那就说明原来的数已经很小很小，接近与0了

比如0.00000000000000000000000000000..............1

那么这个时候，还原的时候有效数字M不再加上第一位的1，而是还原为0.xxxxxxx的小数。这样做是为了表示+-0，和上面那种接近与0的很小的数字。

③E全为1

?这时说明原来的数很大，比如数字

1111...........1.0,那么直接认为这个数就是+-无穷大，（正负取决于符号位）

那么关于浮点数的存储到这里就基本完成了，也就可以解释开篇我们的疑问了我们来看一下。

4.对例子答案的解释?

?

?

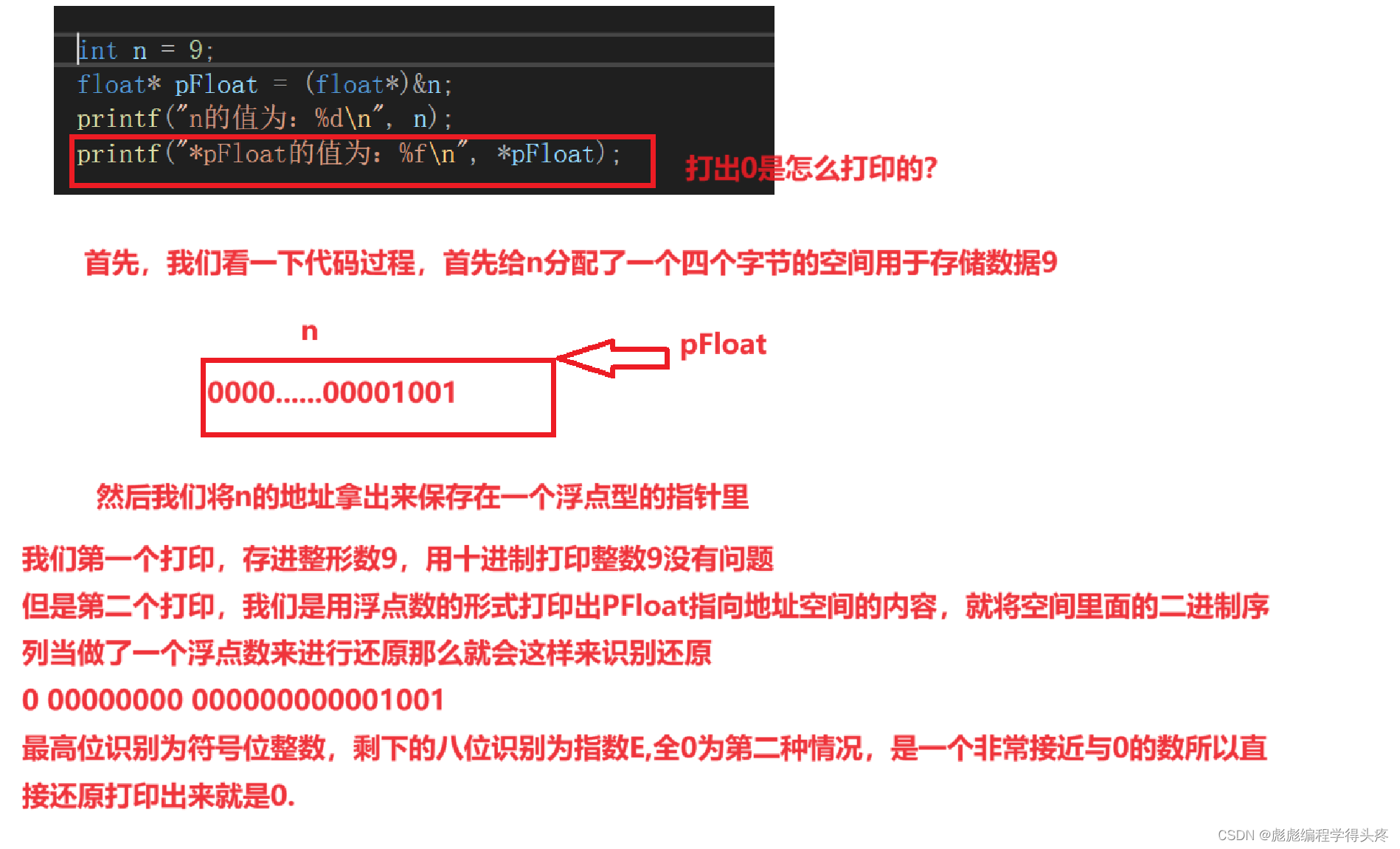
以上就是本期的所有内容，欢迎大家指正。?