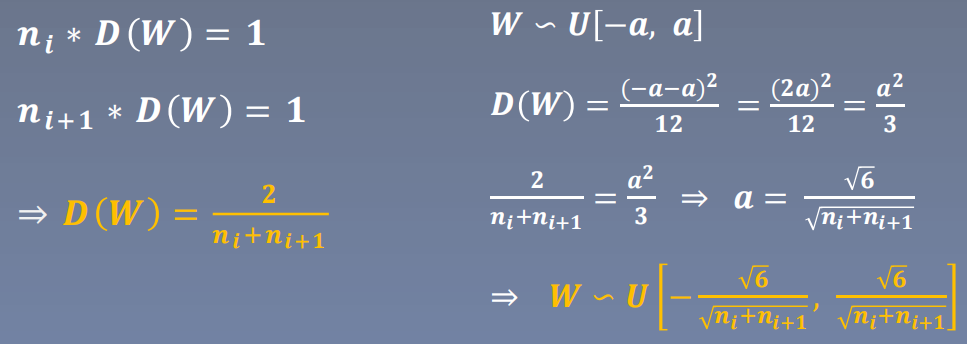pytorch06:权重初始化

目录
一、梯度消失和梯度爆炸
1.1相关概念
一个简易三层全连接神经网络图和神经元计算如下:
观察第二个隐藏层的权值的梯度是如何求取的,根据链式法则,可以得到如下计算公式,会发现w2的梯度依赖上一层的输出值H1;
当H1趋近于0的时候,W2的梯度也趋近于0;—>梯度消失
当H1趋近于无穷的时候,W2的梯度也趋近于无穷;—>梯度爆炸
一旦出现梯度消失或者梯度爆炸就会导致模型无法训练;
1.2 代码实现
import os
import torch
import random
import numpy as np
import torch.nn as nn
from common_tools import set_seed
set_seed(1) # 设置随机种子
class MLP(nn.Module):
def __init__(self, neural_num, layers):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
for (i, linear) in enumerate(self.linears):
x = linear(x)
# x = torch.relu(x)
# x = torch.tanh(x)
print("layer:{}, std:{}".format(i, x.std())) # 打印当前值的标准差
if torch.isnan(x.std()): # 判断是什么时候标准差为nan
print("output is nan in {} layers".format(i))
break
return x
# 权值初始化函数
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear): # 判断当前网络层是否是线性层,如果是就进行权值初始化
nn.init.normal_(m.weight.data) # normal: mean=0, 控制标准差std在1左右
# nn.init.normal_(m.weight.data, std=np.sqrt(1 / self.neural_num))
# =======这段代码的目的是通过均匀分布初始化并结合tanh激活函数的特性,为神经网络的某一层(线性层)初始化合适的权重
# a = np.sqrt(6 / (self.neural_num + self.neural_num))
# tanh_gain = nn.init.calculate_gain('tanh')
# a *= tanh_gain
# nn.init.uniform_(m.weight.data, -a, a)
# 将权重矩阵的值初始化为在 [-a, a] 范围内均匀分布的随机数。这个范围是通过之前的计算和调整得到的,目的是使得权重初始化在一个合适的范围内
# nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)
# ================凯明初始化方法================
# nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num)) # 适合relu激活函数初始化 凯明初始化手动计算方法
# nn.init.kaiming_normal_(m.weight.data)
# flag = 0
flag = 1
if flag:
layer_nums = 100 # 100层线性层
neural_nums = 256 # 每增加一层网络 标准差扩大根号n倍
batch_size = 16
net = MLP(neural_nums, layer_nums)
print(net)
net.initialize()
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
output = net(inputs)
print(output)
1.3 实验结果
这里的初始化使用的是标准正态分布normal: mean=0, 控制标准差std在1左右的方法;

当输出层达到33层后就会出现梯度爆炸,超出了数据精度可以表示的范围。
1.4 方差计算

1.期望的计算公式
2,3.是方差的计算公式
根据1,2,3,可以得出,x,y的方差计算公式,当x,y的期望值都为0的时候,x,y的方差等于x的方差乘以y的方差。
1.5 标准差计算

通过计算可以得出每增加一层网络,标准差增加
n
\sqrt{n}
n?,n也就是神经元的个数;
代码展示:
if flag:
layer_nums = 100 # 100层线性层
neural_nums = 256 # 神经元个数 每增加一层网络 标准差扩大根号n倍
batch_size = 16
执行结果:
可以看出第一层标准差是15.95,第二次标准差在上一层的基础上再乘以
256
\sqrt{256}
256?;

1.6 控制网络层输出标准差为1
从1.5可以看出D(H)的大小有三个因素决定,分别是n、D(X)、D(w),所以只要保证这三者乘积为1,就可以保证D(H)的值为1;

当我们权值的标准差为
1
/
n
\sqrt{1/n}
1/n?,那么就能保证网络层每一层的输出标准差都为1;
代码实现:
输出结果:

通过输出结果可以发现,几乎每一层网络输出的标准差都为1.
1.7 带有激活函数的权重初始化
在forward函数里面添加tanh激活函数

执行结果:
增加tanh激活函数之后,随着网络层的增加,标准差越来越小,从而会导致梯度消失的现象,下面将说明Xavier方法与Kaiming方法是如何解决该问题。

二、Xavier方法与Kaiming方法
2.1 Xavier初始化
方差一致性:保持数据尺度维持在恰当范围,通常方差为1
激活函数:饱和函数,如Sigmoid,Tanh
Xavier初始化公式如下:
代码实现:
手动代码实现

直接使用pytorch提供的xavier_uniform_函数方法
nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)
执行结果:

可以看到,每一层的网络输出标准差都在0.6左右
2.2 Kaiming初始化
当我们使用带有权值初始化的relu激活函数时,输出结果如下,会发现标准差随着网络层的增加逐渐减小,Kaiming初始化解决了这一问题。


方差一致性:保持数据尺度维持在恰当范围,通常方差为1
激活函数:ReLU及其变种
公式如下:
代码实现:
# ================凯明初始化方法================
nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num)) # 适合relu激活函数初始化 凯明初始化手动计算方法
# nn.init.kaiming_normal_(m.weight.data) # 使用pytorch自带方法
输出结果:

2.3 常见的初始化方法
- Xavier均匀分布
- Xavier正态分布
- Kaiming均匀分布
- Kaiming正态分布
- 均匀分布
- 正态分布
- 常数分布
- 正交矩阵初始化
- 单位矩阵初始化
- 稀疏矩阵初始化
三、nn.init.calculate_gain
主要功能:计算激活函数的方差变化尺度(也就是输入数据的方差/经过激活函数之后的方差)
主要参数
? nonlinearity: 激活函数名称
? param: 激活函数的参数,如Leaky ReLU
的negative_slop
代码实现:
flag = 1
if flag:
x = torch.randn(10000)
out = torch.tanh(x)
gain = x.std() / out.std() # 手动计算
print('gain:{}'.format(gain))
tanh_gain = nn.init.calculate_gain('tanh') # pytorch自带函数
print('tanh_gain in PyTorch:', tanh_gain)
输出结果:

总结:任何数据在经过tanh激活函数之后,方差缩小大约1.6倍。感兴趣的话也可以使用relu进行实验,最后我的到的结果方差尺度大约是1.4左右。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 带领残障朋友穿“粤”两千年,沉浸式体验传统文化魅力
- 原生微信小程序,实现方格验证码输入框
- Freemarker模板导出docx
- 深度解析 Compose 的 Modifier 原理 -- ParentDataModifier
- 案例147:基于微信小程序的酒店管理系统
- 【SSM项目】云平台资源管理系统
- 学习使用layPage, 多功能JS分页组件/插件的方法
- SQL NULL值的比较
- 计算机操作系统-第十八天
- 可碧教你C++——位图